模糊决策理论在公路桥梁养护决策中的应用

方金苗，韩治勇，李文丽

(1.皖西学院 建筑与土木工程学院，安徽 六安 237012；2.安徽华裕工程咨询有限公司，安徽 六安 237000)

随着城镇化进程的加速及交通基础工程的发展，目前我国在役桥梁已达80多万座，高等级公路桥梁由于交通量大、车速较高的特点要求养护工作必须要有较高的养护管理体制，而目前我国的公路养护模式单一、管理相对滞后、技术水平偏低、机械化程度不高，加之部分早期兴建桥梁的技术标准较低，建设时间较长，对桥梁管养工作提出了巨大挑战[1-4]。

公路桥涵养护规范将在役桥梁划分为五类[5]，并明确了各类桥梁的养护对策。在实际工作中，一般公路桥梁管养单位维管的桥梁众多，分属不同的道路上，很多座桥梁都需要中修，管养单位如何科学合理确定待修桥梁的优先顺序？因此，研究先进的桥梁评价养护体系是非常必要的。目前大多由公路管理局下的养护队根据自身经验确定，随意性较大，明显缺乏科学性、合理性。实际上合理确定桥梁维修的先后顺序应该考虑桥梁交通状况、桥梁损伤情况以及桥梁维修难度、成本及预期寿命等多因素，实质是一个多目标模糊决策的问题[6]。

针对这一问题，本文引入模糊数学的评价方法，对影响桥梁维修决策的各因素进行了综合分析，对各影响因素指标化，并根据公路桥涵养护规范及相关文献确定各因素指标的权重，采用影响具体决策的多指标模糊评价模型进行综合评价，使评价采用的诸多信息指标数量化、决策过程程序化、实用化，通过一系列的模糊评价、决策，从而依据量化计算分析结果得出最优的决策方案。

1 模糊优选决策模型

模糊综合法以模糊数学为基础，应用模糊关系合成的原理将一些边界不清、不易定量的因素定量化进行评估，常常被用于复杂多变，因素多样的事物，对事物不可量化的因素指标做出定性的判断。通过模糊综合评估，较好地解决了事物的模糊性与算法的确定性这一矛盾，从而为确定桥梁加固顺序提供了较好的思路，也体现出了用模糊数学来评估桥梁工作性能的可行性[7-8]。

1.1 决策指标集的建立

指标集是以影响优选对象的各种因素或者是目标为元素组成的集合[9-10]。由于影响对在役桥梁的状况评价因素较多，评价指标选择时根据公路桥涵养护规范确立影响桥梁主要结构的因素指标，对于间接影响桥梁主体结构的因素以适当大小的权重加以考虑，同时对次要的、影响小的因素作必要的删减，以突出主要决策因素。因此选用桥梁维修决策指标集为：U={u1,u2,u3,u4,u5,u6}={交通量，交通组成即重载交通比例，路面状况，桥梁主件损伤状况，桥梁次要部件损伤及对重载交通影响下主件的恶化趋势的重要程度，现状桥承载能力预估降低程度}。

1.2 确定权重集

一般而言，各影响因素对决策结果的影响程度是不一样的，为体现各个因素重要性的差异，对各指标赋予一定的权重数值，由各量化的权重组成的集合，称为权重集[11-13]。各因素的权重数值可以采用专家打分评定法，也可以采用AHP及复合型方法。本文权重的大小是根据公路桥涵养护规范及相关文献综合确定[14-15]。各影响因素权重为A={a1,a2,a3,a4,a5,a6}=(0.10,0.18,0.12,0.30,0.18,0.12)。

1.3 确定评价集

对于在役桥梁维修排序的优选顺序，针对排序对象，在考虑影响因素的前提下，给出的评语等级为7级：V={延后，缓，延缓，一般，较优，优先，最优先}={-3，-2，-1，0，1，2，3}。因此可确定各评价对象的每个因素对于各评价等级的符合程度称为隶属度，由已经确定的指标集与评价集就可构造出对应的隶属度矩阵R。

1.4 综合评判

每一个待评估对象都对应着一个评价性评语，评价性评语不是具体数值，而是概略性描述，具有一般模糊性[16-18]，如图1表示事件k的概率曲线图，从图上可以直观地看出事件k属于评价性评语b，但函数曲线图同时也反映出，事件k属于评价性评语b是一大概率事件，同时也存在属于a、c的相对较小的概率，这就是评价性评语具有的模糊性。

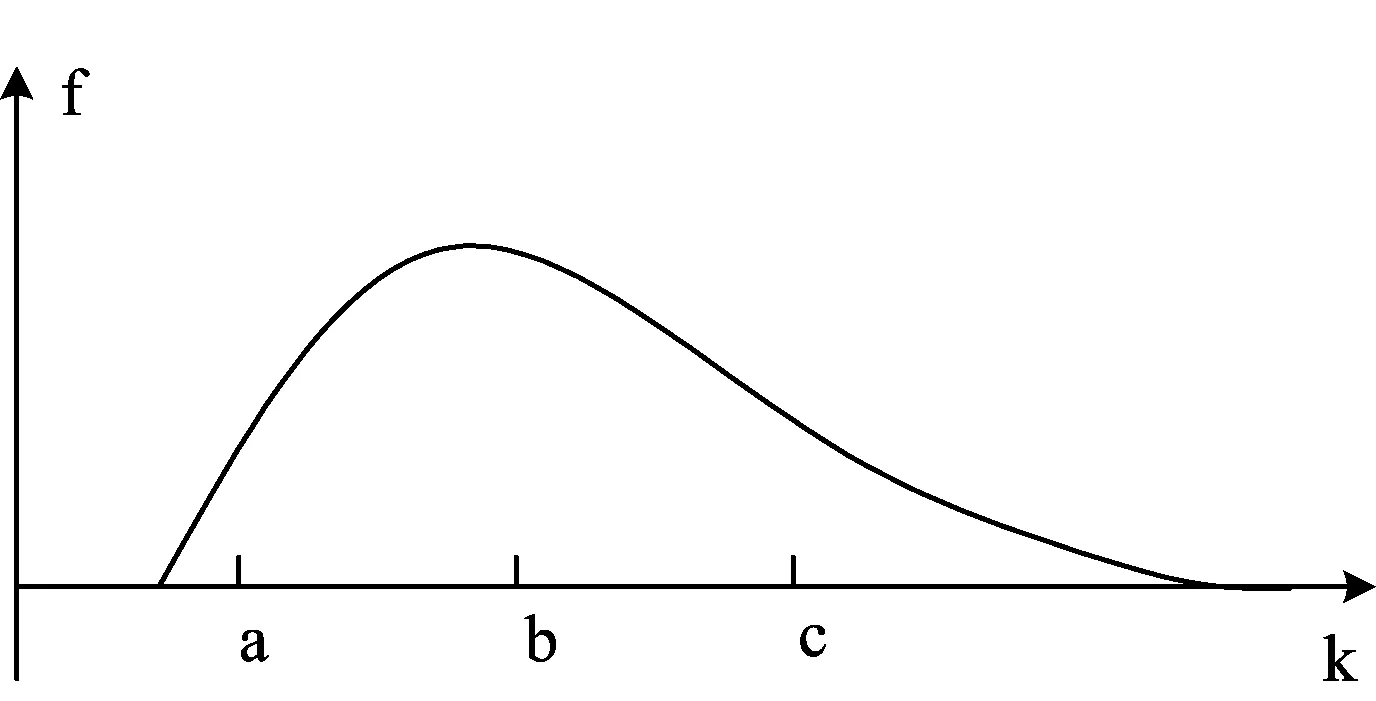
图1 事件k的概率曲线图

根据这一特性，可以按一定原则确定模糊变换关系为：

综合评判关系式为：

其中R为评判矩阵；bj有多种运算形式，本文采用的综合评判关系为加权求和型，其综合的信息全面，符合工程实际。

1.5 计算总综合评价值

各待评估对象最后得分W，计算方法如下：

式中：Wi——第i个桥梁的综合评价值；

Bi——第i个桥梁的综合评判矩阵；

总综合评价值按下式计算：W=∑Wi

W值的大小，即待评估对象的先后顺序。

2 公路桥梁养护优先排序实例

金叶公路建设时间久远，长达几十年，笔者根据金叶公路的5座三类桥梁为例，说明评定计算过程，桥梁的现行状况如下：

金叶1桥：为50米跨钢筋混凝土拱桥，交通量不大，但重载交通比例较高，达到35%，桥面铺装层混凝土多处脱落，部分露筋，铺装层损坏超过15%，台背与桥面有3～4 cm落差，形成跳车，桥梁主拱圈露筋而截面减小，造成的原因主要是重载交通与桥面不平，在桥台处表现明显，拱脚处混凝土有明显开裂，如开裂进一步发展会严重影响主拱圈结构，根据经验估计桥梁本身承载能力已降低近10%；

金叶2桥：为2×20米的钢筋混凝土简支T梁桥，交通量很大，重载交通比例达到20%，桥面铺装层混凝土部分露筋，主梁横向连接处部分有较明显裂缝，一侧桥台有轻微的下沉，估计桥梁承载能力已降低8%；

金叶3桥：为3×16米的钢筋混凝土T梁桥，交通量大，重载交通比例为25%，桥梁铺装层混凝土露筋，铺装层损坏超过10%，桥台混凝土支座有露筋、开裂剥落现象，全桥估计承载能力下降6%；

金叶4桥：为3×10米的钢筋混凝土简支板梁桥，交通量大，重载交通较少，桥面铺装层混凝土部分脱落，桥面裂纹较多，主梁支座接头处有明显裂缝，板梁横向接处有裂缝，一端桥台有轻微下沉，估计桥梁承载能力已下降8%；

金叶5桥：为3×13米钢筋混凝土简支板梁桥，交通量大，重载交通比例为15%，桥面铺装层混凝土有脱落、主梁桥梁有露筋现象，2桥台均有轻微下沉，估计桥梁承载能力已下降10%。

根据公路桥涵养护规范，五座桥梁均为三类桥梁，需要进行维修加固处理。公路养护部门可以采用模糊决策理论进行优化排序。根据平时经常检查、定期检查记录得到各个桥梁的综合评判，分别考察各因素时，经各考察对象间横向比较可得到确定优先级的逻辑推理评语如表1，根据模糊理论确定逻辑推理的模糊映射隶属度等级如表2。

按照从V到U的模糊映射关系，得出各座桥梁的评判矩阵即各座桥对应于评判关系为：

表1 对各座桥梁的逻辑推理评语

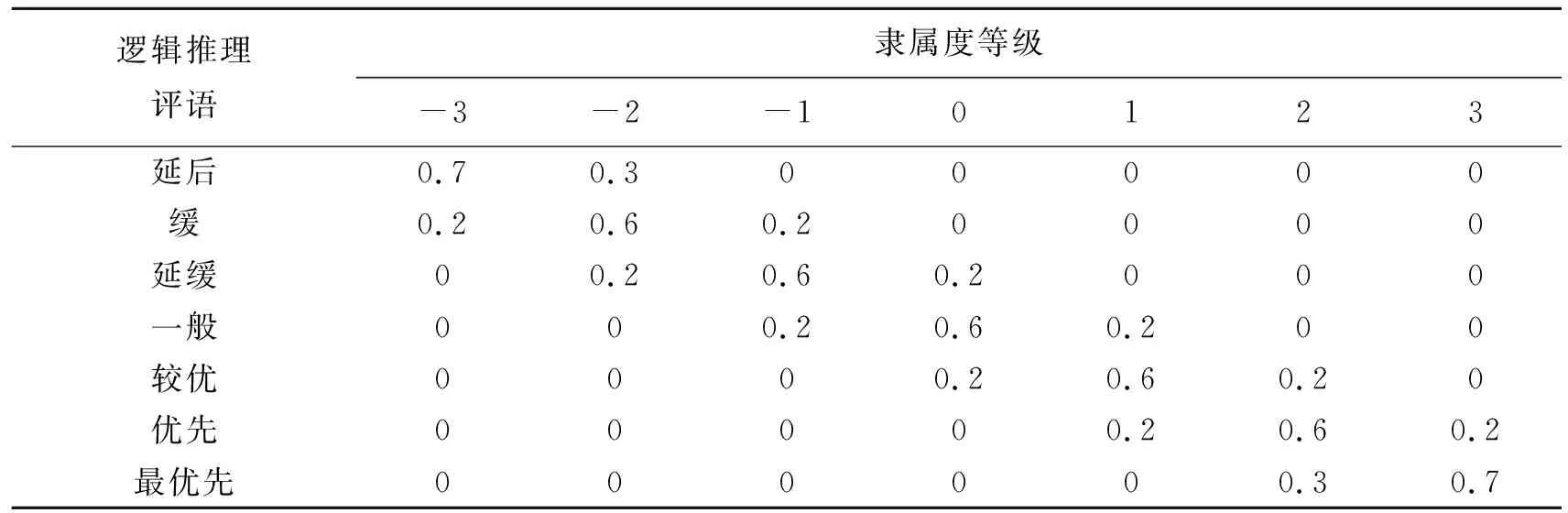
表2 集合U、V的模糊映射关系

由模糊优选决策模型，在各影响因素权重A、优选对象对于评价指标的隶属度R及评价集V已经确定的情况下，对各优选对象的模糊优选综合评价值计算如下：

(1)

同理其他四座桥的模糊综合评价值为：

对5座待维修桥梁的模糊综合评价，经(1)—(5)式计算各桥的综合评价值W，从金叶1桥到金叶5桥分别为2.33，2.28，1.4，1.28，1.904。由此可明确确定各座桥维修顺序，即待维修桥梁的先后顺序分别为金叶1桥、金叶2桥、金叶5桥、金叶3桥、金叶4桥。

3 结语

根据上述分析，可以得到如下结论：

1)模糊决策模型在公路桥梁养护中的应用，可以有效地反映出待维修桥梁需要维修的优先等级，使得在确定桥梁维修时的决策更科学、合理、明晰，进而提高桥梁维修保障效率。

2)从文章计算分析可以看出，方案优选的结果在合理简化因素后，取决于各参与因素的权重，因此，各相关权重取值应力求科学、合理，可以借鉴以往工程资料，梳理分析出各因素的相对重要性，并结合相关专家的建议，确定各权重数值。

3)针对实际情况，可以引进更多合理的指标并重新分配权重，使模糊决策模型考虑得更全面。

4)本文的评估模型还有待于对其他桥梁评估检验，各因素的隶属度和权重的确定还需要做进一步的研究。特别是研究适应大多数桥梁的综合评估方法仍旧是今后研究的热点。