问题成串促思维 模式化归显身手

☉湖北省武汉市汉阳区教育局教科中心 桂文通

问题是数学教学的心脏，是学生思维的中心，在数学课堂教学中，需要我们教师提供有价值的问题.“我所解决的每一个问题都将成为一个模式，以用于解决其他相关问题”（笛卡尔语），运用模式识别，自觉化归是问题解决的一个有效途径，可以很好地实现高效解题的目的.

问题串是指在一定的学习范围或主题内，围绕一定目标、按照一定的逻辑结构，精心设计的一组问题.问题串教学是引导学生带着任务积极地自主学习，由表及里，由浅入深地自我建构知识的过程.因此，问题串的设计应体现知识与方法的过渡性，根据教学目标，把教学内容编设成一组组、一个个彼此关联的问题，使前一个问题作为后一个问题的前提，后一个问题是前一个问题的继续、发展或补充，这样的问题组合在一起为学生搭建了一个思维的阶梯，使学生在问题串的引导下，实现由未知向已知的转变，让学生在明确知识内在联系的基础上获取基础知识，提升思维能力，促进思维纵向深入的发展.

模式识别解题的心理机制是当学生主体接触到数学问题之后，首先要辨别题目的类型，以便与已有的知识和经验发生联系，然后确定解决问题的思路.模式识别过程是感觉信息与长时记忆中的有关信息进行比较和分析，判断和决策它们的最佳匹配的过程.在学习数学过程中，学习者所积累的知识、方法、经验经过加工、融合，会得出具有长久保存价值的或基本的典型结构与重要类型——模式.从解题思想的角度看，模式识别解题其实是化归思想的运用，具体体现是化陌生为熟悉，化未知为已知，化新的问题为已经解决的问题，它的思维过程大致可以用图1表示.

图1

基于以上解题观念，笔者设计了一节与正方形有关的复习示范课.

问题1：如图2，在正方形ABCD中，E是AD上一动点，G是BE上一动点，过点G作BE的垂线分别交AB，CD于点H，F.求证BE=HF.

学生探索思路：

经过点C作CM∥HF交AB于点M，易证四边形CFHM是平行四边形，由△BCM △ABE，得HF=CM=BE.

设计意图：提出本节课的基本问题，也是这节课的源问题.让学生熟悉证明线段相等的常见方法（全等、平行四边形或等腰三角形等知识），由证明过程知我们可以提炼一个互逆结论：在图2中，若BE⊥HF，则BE=HF；若BE=HF，则BE⊥HF.

问题2：在边长为6的正方形ABCD中，点F为CD上一点，且DF=2.

（1）如图3，将正方形ABCD沿MN对折，点A刚好落在点F处，求折痕MN的长；

（2）如图4，E是AD的中点，在BC上找点G，使EG=AF，写出BG的长.

学生模式解决：

（1）由折叠的性质知AF⊥MN，直接回到问题1的模式，所以由问题1的结论得

（2）根据问题1的结论，可过点E作EG⊥AF交BC于点G，则有EG=AF，再求BG的长.此时过点G作GM⊥AD，垂足为点M，可求出BG=AM=AE-ME=AE-DF=3-2=1.另外，点G关于BC边的中垂线的对称点G′也满足条件，此时BG′=5.所以满足条件的G点有两个，故BG=1或BG=5.

设计意图：（1）改变问题的呈现方式，用折叠代替垂直，要求学生能够根据条件自觉地将问题进行转化；（2）提供了一个开放性的问题，要求学生克服思维定式的影响，关注学生思维的严谨性.在无图的情况下，当EG=AF时，EG与AF不一定满足垂直关系，不止有一条线段，而是一组对称线段.

问题3：在问题1中，如图，平移HF，使DE=DF，若EG=4，FG=6，求四边形DFGE的面积.

学生探索思路：

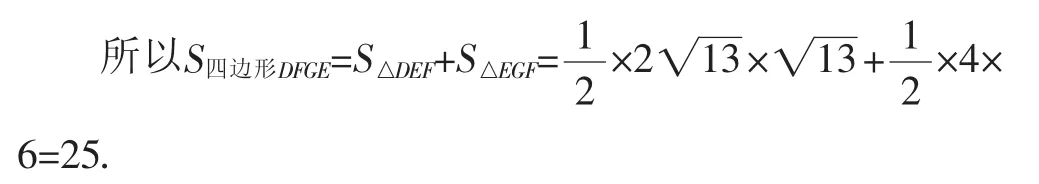
方法2：（旋转法，将四边形转化为正方形）如图6，连接DG，过点D分别作DP⊥EG，DH⊥GF，垂足分别为点P，H.易证△PDE △HDF；△PDG △HDG.于是PE=HF，PG=GH，且四边形PDHG是正方形，.

因为EG=4，FG=6，所以GH=5.于是S四边形DFGE=S四边形DPGH=52=25.

方法3：（旋转法，将四边形转化为等腰直角三角形）如图7，延长GF至点M，使MF=EG.可证△GDE △MDF；△MDG是等腰直角三角形.于是5=25.

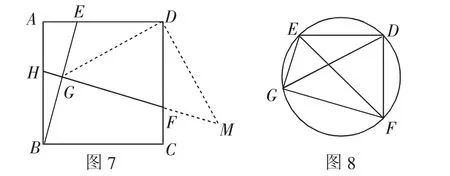
设计意图：将基本问题特殊化，提炼一个基本图形：一组邻边相等，且对角互补的四边形.图5中的四边形DEGF的四个顶点其实在同一个圆上.在图8中，我们可以得到一组互逆命题：若DE=DF，则GD平分∠EGF；若GD平分∠EGF，则DE=DF；并探讨了这个不规则四边形面积的求法.

问题4：如图9，正方形EFGH的顶点E与正方形ABCD的中心O重合，当正方形OFGH绕点O顺时针旋转过程中，OF，OH分别交直线BC，CD于M，N两点.

（1）讨论正方形OFGH在旋转过程中，四边形OMCN的面积的变化情况；

（2）讨论线段OM、ON的数量关系；

（3）讨论线段CN、CM、OC之间的数量关系.

学生模式解决：

分析问题条件，四边形OMCN具有图8的特征，由问题3的解决思路可知：

（1）S四边形OMCN=S△OBC，所以正方形OFGH在旋转过程中，四边形OMCN的面积不变；

（2）OM=ON；

设计意图：让学生自觉地寻找熟悉的基本图形，运用已经学会的方法解决新情境下的问题.

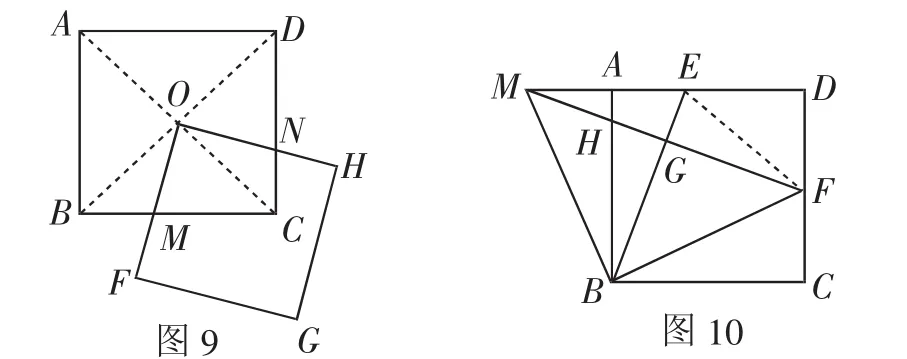
问题5：如图10，在问题1中，分别延长FH，DA交于点M.若AM=CF，请你试着发现图中结论！

学生发现结论：

（1）△ABM △CBF；

（2）△FBM是等腰直角三角形；

（3）∠EBF=45°；

（4）△EBM △EBF；

（5）BE平分∠AEF，BF平分∠CFE；

（6）点B到直线EF的距离等于正方形的边长；

（7）AE+CF=EF；

（8）△DEF的周长是一个定值，且等于正方形周长的一半；

……

设计意图：“当你找到第一个蘑菇后，要环顾四周，因为它们总是成堆生长的”（波利亚语）.在基本图形中强化条件，综合问题1、3中的基本图形，开放结论，要求学生根据条件合理联想与推理，发现基本图形与基本结论，培养学生的发散思维能力.

问题6：（1）如图11，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，AD=6，求直角梯形ABCD的面积.

学生模式解决：

根据已知条件，可以将梯形ABCD补成正方形ABCF.又因为∠DCE=45°，由学生的发现7可知BE+DF=ED.

设BC=x，则AE=x-4，DF=x-6.

由BE+DF=ED，BE=4，得DE=（x-6）+4=x-2.

本次研究以2015—2017年的卫生人才数量作为基础，预测2019—2021年东丽区卫生人才的需求情况，预测东丽区2021年卫生人才的数量将超过2 250人，见（表2）。

在Rt△ADE中，AD2+AE2=DE2，所以62+（x-4）2=（x-2）2，解得x=12.

于是S梯形ABCD=+12）×12=108.

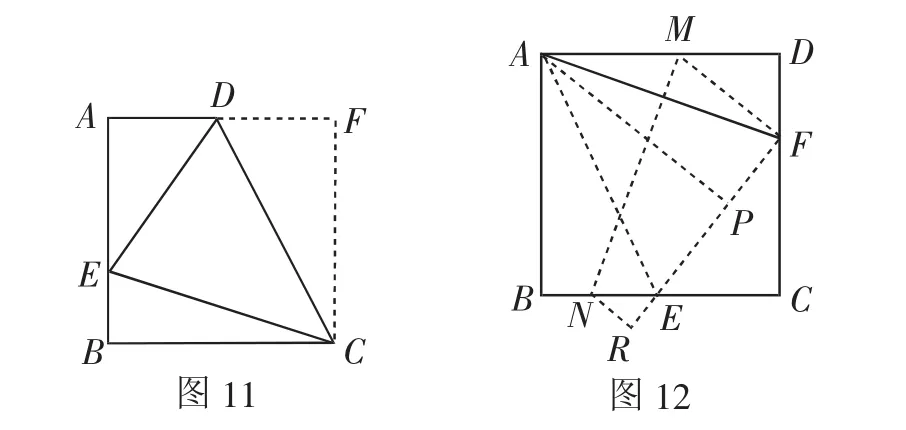
（2）如图12，在问题2（1）中，AB的对应边FR交BC边于点E，若任意改变点F的位置，试研究△CEF的周长的变化情况.

学生模式解决：

由折叠的性质知∠BAF=∠AFE.又因为AB∥CD，所以∠BAF=∠AFD，故∠AFD=∠AFE（类似问题5中的结论5）.

过点A作AP⊥EF，则AP=AD=AB（类似问题5中的结论6）.

于是可证△ABE △APE，△ADF △APF，得BE=PE，DF=PF.

所以△CEF的周长=CE+CF+EF=CE+CF+PE+PF=CE+BE+DF+CF=BC+CD=2BC（定值）（类似问题5中的结论8）.

设计意图：（1）直接根据条件将特殊直角梯形转化为正方形，由特征角“∠DCE=45°”联想到基本结论“BE+DF=ED”，再运用方程知识设元求解；（2）挖掘折叠对称图形中隐藏的结论“AF平分∠DFE”，再自觉地运用问题5的方法求解.

至此，本节课的问题结构关系与解决的过程可以用图13呈现：

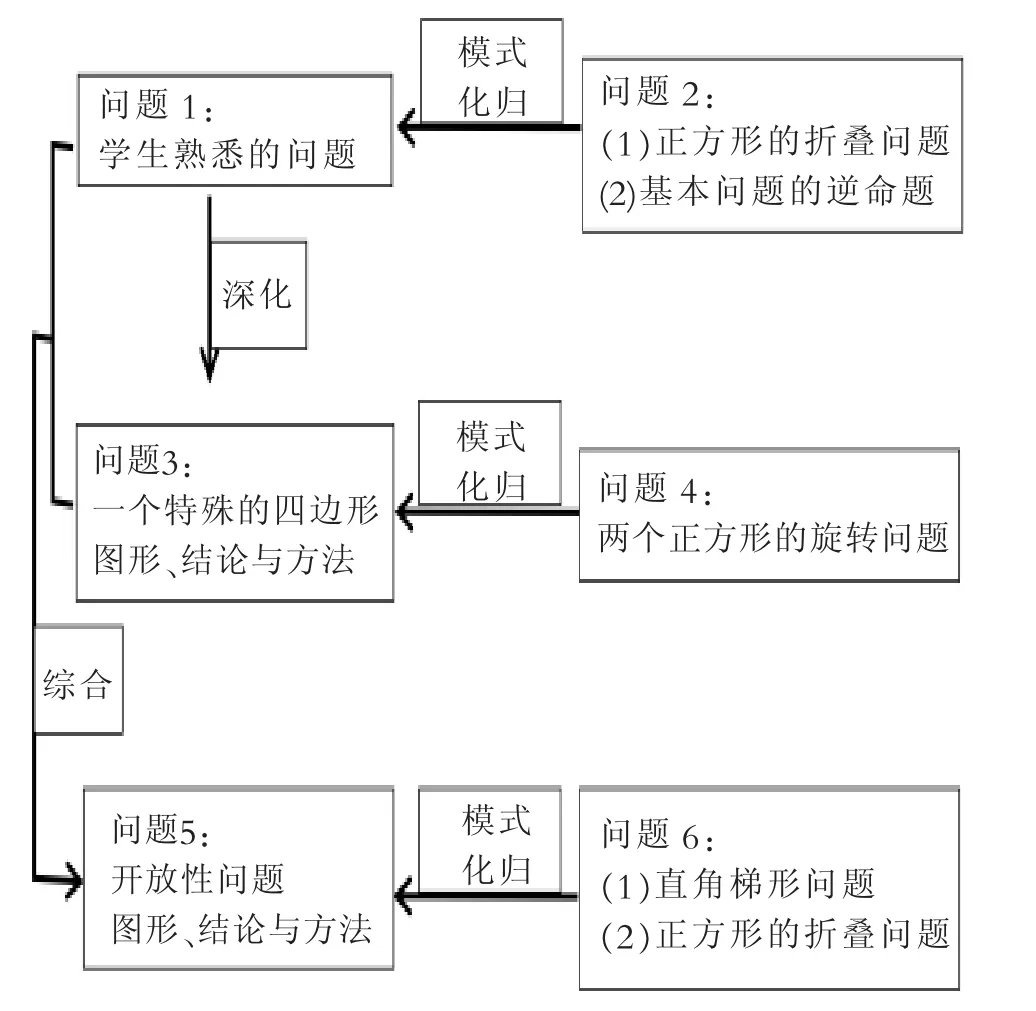
图13

从课堂教学效果看：设置具有价值的问题串是数学课堂的灵魂，有效的问题串的设计和运用决定着我们的教学方向，关系到学生思维活动开展的深度和广度，实现了解题教学的高效.数学是一种模式，我们应该帮助学生识别这种模式，坚持模式识别教学，提高学生数学解题能力，带领学生走出题海，真正学会解题，让学生享受数学解题的快乐！