各向异性加权先验模型MAP投影域降噪

李安迪，刘 祎，张 权，桂志国

1.中北大学 山西省生物医学成像与影像大数据重点实验室，太原 030051

2.中北大学 信息与通信工程学院，太原 030051

1 引言

计算机断层扫描技术（Computed Tomography，CT）的出现极大地促进了临床医学诊断的准确性，已成为一种有效而重要的成像手段。但常规剂量的CT辐射对人体有一定的伤害，受检者需要承担未知的健康风险。因此如何在保证CT图像低噪声高分辨率的同时减少射线剂量是CT领域的一个研究方向。降低X射线剂量的主要措施有降低管电流或管电压，增大准直宽度，增大螺距等，最简单有效的措施为降低管电流。然而由于管电流降低，探测到的光子数会随之减少，投影数据会被大量的量子噪声污染，使得重建图像质量严重下降，干扰临床医学诊断的准确性[1]。目前对这一问题，主要有三种解决途径：（1）图像后处理，对重建出的图像直接去噪；（2）对噪声特性进行建模，用迭代法进行重建；（3）投影域处理，对经过降噪处理后的投影域数据进行直接FBP（Filter Back Projection）重建[2]。

图像后处理的优点在于不需要获得投影数据而可直接对重建图像降噪。在这一方向，Li等人[3]提出了一种改进的RSF（Region-Scalable Fitting）模型，将其与稳健统计方法相结合，获得了良好的去噪效果，且收敛速度更快；Chen等人[4]提出针对低剂量腹部CT图像的大尺度加权强度平均（Weighted Intensity Averaging over Large-Scale Neighborhoods，WIA-LN）算法，利用在大尺度邻域中具有与目标像素相似周围结构的像素加权强度平均值来更新目标像素，取得了较好的视觉效果；后于2014年将字典学习应用于低剂量CT图像域处理中，提出 ASDL（Artifact Suppressed Dictionary Learning）算法，利用伪影的方向和尺度信息训练出伪影原子，再与组织特征原子结合建立三个判别字典，可有效去除条形伪影[5]。第二种方法的优点在于考虑了投影数据的统计特性。针对此，Wu等人[6]提出一种新的迭代CT重建算法，该算法利用K-稀疏自动编码器（K-Sparse Auto-Encoder，K SAE）从FBP重建出的常规CT剂量图像中学习一种非线性稀疏先验，基于此先验进行迭代重建；受压缩感知理论和TV最小化的影响，Xu等人[7]在统计迭代重建框架中，将冗余字典中的系数约束纳入目标函数中，在降低噪声和保护细节结构特征方面都取得了较好的效果；Makeev等人[8]将基于惩罚似然目标函数和Huber先验的统计迭代重建算法应用于胸部CT中，取得了较好的结果。但迭代算法计算量大，成本昂贵。针对第三种方法，Lauzier等人[9]研究了先验图像约束压缩感知在CT剂量减少时的应用，得到了较好的去噪效果；Chen等人[1]提出一种应用于低剂量CT图像重建的自适应加权非局部先验模型，可自适应选择利用图像全局信息，在分辨率保持和噪声去除之间取得较好的平衡。Zhang等人[10]提出一种低剂量CT联合去噪算法，原始投影数据经过广义Anscombe变换（Generalized Anscombe Transform，GAT）后，所含噪声可视为具有同一方差的加性独立高斯白噪声，用BM3D对其滤波，对所得到的投影数据作GAT反变换，FDK重建后再进行RNLM滤波处理，所得结果与原始图像较为接近；2012年，Zhang[11]等人提出一种基于各向异性加权先验模型的最大后验（Maximum A Posteriori，MAP）正弦图平滑算法，将各向异性扩散系数与传统的二阶PM先验模型相结合构造出新的正则项，最后用高斯-赛德尔法来求解基于此先验模型的MAP正弦图优化模型。该算法虽然能依据不同区域自适应地调节平滑程度，有效减少条形伪影，但视觉上伪影依然明显且边缘已经模糊。

近年来，直觉模糊集在图像处理中取得了广泛的应用，Atanassov[12]首次提出了直觉模糊集的概念。直觉模糊熵作为直觉模糊集的测度，能够较好地描述信息的确定性与不确定性。图像过渡区域本身存在模糊性，即不确定某一像素是否属于平坦区域，给图像处理带来不便。对此Chaira[13]提出利用直觉模糊熵检测图像边缘，区分平滑区域和细节区域；上官宏[14]定义了正弦图的局部直觉模糊熵，并将其应用于正弦图平滑算法中。受上述算法启发，本文提出一种融合了直觉模糊熵的各向异性加权先验模型，并将其与MAP优化估计算法框架结合，实现对投影数据不同区域进行不同强度的降噪处理。

2 算法原理

2.1 MAP降噪算法模型

MAP是通过最大化后验概率分布函数来求解目标最优值。将经系统校正和对数变换后的低剂量投影数据看作q，去噪后投影数据看作 f，其可建模成一个马尔科夫场。根据Bayesian理论可得后验概率分布为：

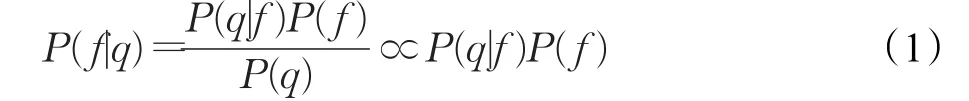
由此实现 f的估计，可建立如下优化模型：

近年来确定待估计参数 f的先验分布P(f)一直是众多学者研究的热点，也是MAP估计框架的关键点。将 f建模成一个马尔科夫随机场（Markov Random Field，MRF），根据 Hammersley-Clifford定理给出的MRF与吉布斯随机场等效的条件，可得到起正则化作用的先验分布项：

其中，Z为配分函数，通常设置为常数1；U(f)为能量函数；Uj(f)代表在去噪投影数据中像素 j处的能量函数值；β为一全局超参数，用来控制先验正则项在优化过程中所起作用的大小。

对式（3）两边取负对数变换得到后验能量函数如下：

文献[14]研究表明，经系统校正和对数变换后的投影数据q近似服从非平稳高斯分布，该投影数据方差为：

其中，rj、fj为与扫描系统相关的参数。采用统计迭代法来估计去噪后的投影数据，有如下似然函数形式：

可得到式（4）中负对数似然函数为：

其中，Σ是以σj为组成元素的对角矩阵。最大后验概率模型可转化为求解如下函数，即通过最小化后验能量函数来实现投影数据的降噪：

2.2 先验模型

一般情况下，能量函数通过邻域中像素间差异的加权和求得：

其中，Nj表示中心像素为 j的邻域；权重ωij表示邻域像素i与中心像素 j间的相关关系。传统的二次方先验模型(u(t)=t2/2)对各个像素无差别对待，由此会造成重建图像边缘模糊和平坦区域过平滑等问题。Huber先验模型可根据图像中心像素与邻域像素的灰度差值进行自适应性平滑，因此本文选用Huber先验模型，其形式如下：

Huber先验模型利用阈值hth来控制图像的平滑程度，当像素差值大于hth时，该区域属于边缘细节区域的可能性更大，采用平滑程度较轻的线性形式；当像素差值小于hth时，该区域属于平坦区域的可能性更大，采用二次项形式加大平滑程度。

权重ωij表示中心像素与邻域内其他像素间的相关关系，通常情况下定义为两个像素间欧式距离的反比。考虑到二维正弦图中探测器探元方向和角度方向上对邻域内像素的影响，且探元方向影响大于角度方向，水平方向权重取1.00，垂直方向权重取0.25，如图1所示。

图1 邻域内权重值

2.3 改进的各向异性加权先验模型

传统二次先验模型不能有效地区分边缘细节区域和平坦区域，不能实现对不同区域的自适应平滑，重建结果中易导致边缘细节区域过平滑，平坦区域平滑力度不足等情况，同时考虑到权重ωij是固定不变的，提出一种融合了各向异性扩散系数的Huber先验模型：

常用的各向异性扩散系数有如下形式：

正弦图中平坦区域和边缘细节区域区分不明显，即本身具有模糊性。根据直觉模糊集理论，将正弦图看作直觉模糊集合，某一像素j对该直觉模糊集合的隶属度φ(j,γ)、非隶属度 η(j,γ)和犹豫度 ρ(j,γ)定义如下：

构造出正弦图的局部直觉模糊熵：

K衡量像素点 j在正弦图中处于平坦区域还是细节区域，K值越大，像素点 j处于细节或边缘区域的确定性越大；反之K值越小，像素点 j处于平坦区域的确定性越大。

综合考虑正弦图的梯度模、局部方差与局部直觉模糊熵，可构造一种新的各向异性扩散系数：

根据以上各向异性扩散系数的扩散特点，此先验模型可对正弦图进行自适应平滑。若像素点 j处于平坦区域，其对应的K值、梯度模均较小值变大，平滑程度加大；若像素点 j处于边缘区域，其对应的K值、梯度模均较大，值变小，平滑程度减弱。因此可有效地在去除噪声的同时，较好地保持图像边缘细节信息。

综上所述，本文提出的新的基于各向异性扩散系数的先验模型为：

根据本文提出的各向异性加权Huber先验模型，式（8）所描述的算法优化模型为：

3 实验结果与分析

本文采用三种体模来验证基于改进的各向异性加权先验模型的MAP投影域降噪算法的有效性：体模1为数字骨盆模型，体模2为Shepp-Logan头模型，体模3为数字胸腔模型（thorax phantom）。采用三种对比算法：经典FBP直接重建算法，Wang等人[15]提出的惩罚重加权最小二乘优化算法PRWLS，Zhang等人[11]提出的各向异性加权先验MAP平滑算法。各模型原始图像如图2所示，体模大小均为512×512。实验所用编程工具为Matlab，版本为R2016a。计算机操作系统为Windows 10 64位操作系统，处理器为Intel®CoreTMi7-7700 CPU@3.60 GHz。

图2 各模型的原始图像

实验中所用模拟投影数据通过等角扇束扫描方式得到，探测器探元弧形排列为888个，顶点距离X射线源949 mm，距离旋转中心408 mm，984个投影角度均匀分布在360°圆周上，因此正弦图大小为984×888。实验过程中所求正弦图方差相关参数为rj=150,η=42 000,迭代次数设置为15次。超全局参数β控制正则项在平滑过程中的作用，本文所提算法对Huber先验不同表达式设置不同的β值，当像素差值大于阈值时，增大β值以加大先验正则项的作用，控制了平滑程度，反之像素差值小于阈值时，β值较小，先验项在对投影数据处理过程中作用较小，平滑程度加大。通过手动调节其值以得到视觉效果最优的重建结果图，各算法β值设置如表1所示。

表1 参数设置

将FBP直接重建算法、PRWLS算法、文献[12]算法和本文算法分别应用于体模1，调整参数得到各个算法对应的最优效果，如图3所示。从结果图中可看出，直接使用FBP算法得到的重建图像被条形伪影覆盖，视觉效果最差；经PRWLS算法重建出的图像视觉效果得到显著提升，但在中心部位条形伪影依然严重；文献[12]算法一定程度上减少了中心条形伪影；本文算法在有效减少中心条形伪影的同时，更好地保持了边缘与细节信息，在左右两侧嵌套的黑白两色圆形处边缘保持更明显。

图3 体模1实验结果图

同样的方法应用于体模2和体模3，图4（a1）～（e1）和图5（a1）～（e1）分别为体模2和体模3用四种方法重建得到的结果，图4（a2）～（e2）和图5（a2）～（e2）为其对应的中心放大图。从体模2的中心放大区域可看出三个白色椭圆区域噪声明显减少，且两个黑色区域部分更平滑；体模3中整体背景部分更平滑，放大部分中可看出在白色椭圆部分尤其是中间椭圆，前三种方法处理后还有可见的黑色噪声点，而采用本文算法则有效去除了噪声点。由此可证明，文献[12]算法在去除噪声方面有明显效果，但本文算法不仅能够有效地去除噪声，且在保持细节与边缘信息方面有更好的效果。以上实验充分说明了了本文算法的有效性。

图4 体模2实验结果图

图5 体模3实验结果图

经过仿真实验验证，本文算法在去除噪声和保护边缘信息方面都有提升。这是由于相对于其他算法，本文算法在对投影数据的处理中结合了局部直觉模糊熵，采用Huber先验模型，更有效地区分了平坦区域和边缘细节区域，使在平坦区域平滑力度加大以有效去除噪声，在边缘细节区域减小平滑力度，保留相关信息。为了进一步说明算法有效性，选取体模中像素值变化较多的行或列进行比较，图6～图8分别给出了体模1在第245行的像素值，体模2在第220列的像素值，体模3在第300行的像素值相对于四种算法的对比。

图6 体模1第245行像素值

由像素值对比图可看出本文提出的基于改进的各向异性扩散Huber先验平滑算法所重建出的图像在边缘和平滑区域与原始干净无噪图像像素值更加接近。为了进一步说明这一问题，图9～图11选取像素值变化平缓区域进行像素值比较。可看出本文算法重建出的图像整体尤其是在中心区域更接近原始图像。

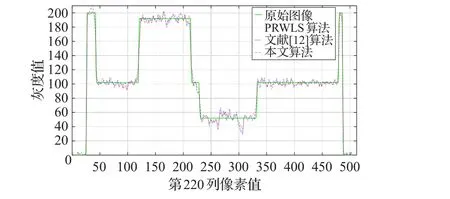
图7 体模2第220列像素值

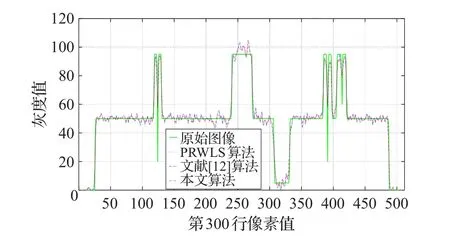
图8 体模3第300行像素值

图9 体模1第310行像素值

图10 体模2第100列像素值

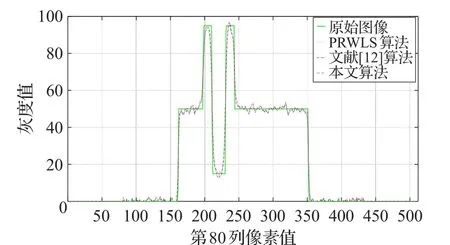
图11 体模3第80列像素值

为了客观说明本文算法的有效性，采用信噪比定量描述各种算法，同时记录了各算法运行时间。计算信噪比所用的公式如下：

表2 各算法客观评价指标

其中，y代表经过算法处理后的图像像素值。表2给出了各种算法的客观评价指标。

由表2可以看出本文算法在信噪比上有明显提升，重建图像质量优于其他算法，且计算速度与文献[12]算法相当，从客观上说明了本文算法的有效性。

4 结束语

本文提出了一种改进的基于各向异性加权先验模型的MAP投影域降噪算法。针对原始算法中使用的二次方先验模型对各个像素无差别对待问题，本文采用Huber先验模型，针对不同的区域进行不同程度的平滑处理。同时考虑到局部直觉模糊熵可有效地区分正弦图中的平滑区域和细节边缘区域，将其与传统的各向异性扩散系数相结合，并采用正弦图局部方差来实现该系数的自适应性调节。最后将其融合于最大后验概率估计模型中，实现对整个正弦图的平滑处理。实验证明，本文算法相对于其他三种算法能够有效去除图像噪声，同时可以有效地保持图像边缘与细节信息，处理得到的图像与原始图像更接近。但同时算法中一些参数也需要根据经验手动调整，可以作为下一步研究的方向。