数列与其他知识交汇命题思路再探

☉江苏省镇江中学 王 磊

近几年高考数学命题特点是注重知识的交汇点和结合点，以及数学知识之间的纵向和横向的有机联系.数列是考查同学们逻辑思维能力和推理能力的好素材，新课标下的高考对数列的考查呈现出综合性强、立意新、难度大的特点，注重在知识交汇点设计问题，考题往“桃李嫁接”的方向发展.下面举例剖析，供参考.

一、数列与推理的交汇

归纳推理是高中数学的重要内容，也是学习高等数学的基础和重要工具.近几年高考加大了对推理与证明的考查力度，而利用归纳推理解决数列问题成为高考的一个新亮点.

例1 在日本东京举行的第52届世乒赛期间，某商店橱窗里用同样的乒乓球堆成若干堆“正三棱锥”形的展品，其中第1堆只有1层，就一个球；第2，3，4，…堆最底层（第一层）分别按图1所示方式固定摆放，从第二层开始，每层的小球自然垒放在下一层之上，第n堆第n层就放一个乒乓球，以f（n）表示第n堆的乒乓球总数，则f（3）=______；f（n）=______（答案用n表示）.

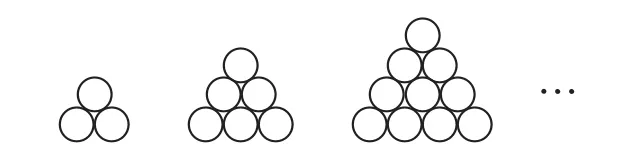
图1

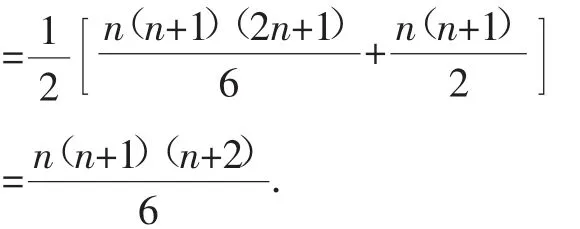
归纳推理是通过对特殊的、具体事物的分析、认识、研究，从而导出一般性结论的方法.在归纳推理中，根据同一个前提，有时可以得出不同的结论，这种结论的正确性有时是很难证明的，而且由几个特殊对象归纳出的结论也不一定正确，还要经过逻辑证明和实践检验.

二、数列与算法的交汇

例2 执行如图2所示，的程序框图，若p=0.8，则输出的n=______.

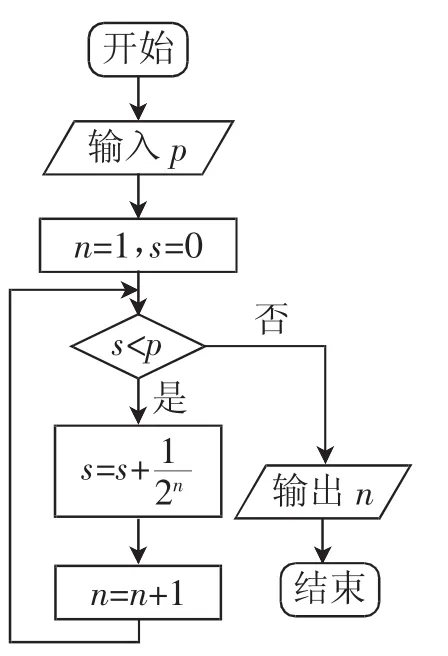
图2

数列与算法的结合考查是高考的一个新“靓点”，在各个省的自主命题中都有体现，同学们在学习时要注意对其规律进行总结，熟练转化为数列问题进行处理.变量追踪法解决问题思路简单，但往往过程烦琐，而且步骤太多时不易操作，但将此题转化为数列求和问题与解不等式问题，就使得解题的艺术性和思想性大大提高.

三、数列与三角的交汇

（1）求数列{an}的通项公式；

（2）设bn=2nan，数列{bn}的前n项和为Tn，求Tn的表达式.

所以Tn=π［（2n-3）·2n+3］.

三角是高中数学中的一个重要内容，也是历年高考的必考知识点，它与数列相结合进行考查的题目类型主要有下面四种：①角A，B，C成等差数列型；②角A，B，C成等比数列型；③三边a，b，c成等差数列型；④三边a，b，c成等比数列型.

四、数列与应用问题交汇

例4 第二届夏季青年奥林匹克运动会于2014年8月16日～28日在江苏南京举行，从社会效益和经济效益出发，某宣传部门决定建立一个“科技展览基地”，并以此发展旅游产业.根据规划，本年度投入800万元，以后每年投入将比上年减少倍.本年度旅游基地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加倍.

（1）设n年内（本年度为第一年）总投入为an万元，旅游业总收入为bn万元.写出an，bn的表达式；

（2）至少经过几年，旅游业的总收入才能超过总投入？

解析：（1）第1年投入为800万元，第2年投入为800×

所以，n年内的总投入为

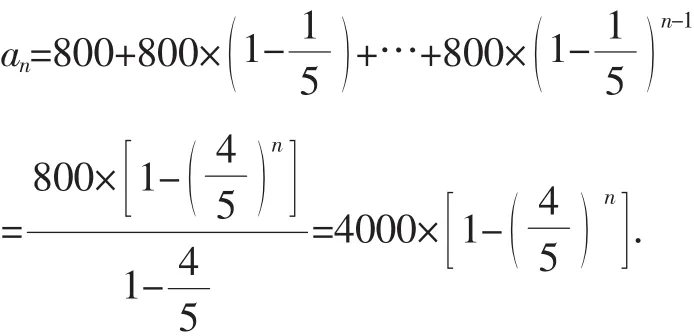
所以需要至少经过5年旅游总收入才能超过总投入.

投资理财中这一类问题通常可归结为等比数列问题，利用等比数列知识求解，但往往要结合函数及不等式知识，对综合能力要求较高.本小题主要考查建立函数关系式、数列求和、不等式基础知识；考查综合运用数学知识解决实际问题的能力.H