用方程的思想解直线与圆锥曲线关系问题两例

☉湖北大学附属中学 李 俊

函数与方程思想是中学数学中重要的思想方法之一，它从问题的数量关系入手，运用数学语言将问题中的条件转化为数学模型（方程（组）），然后通过解方程（组）使问题得到解决.直线与圆锥曲线关系中的许多问题，若能注意运用函数与方程的思想去分析，则往往能居高临下，较快较易地找到解题的突破口，本文举两例加以说明，供大家参考.

例1 已知动点P到点F（1，0）的距离是它到直线x=4的距离的一半.

（1）求动点P的轨迹C的标准方程.

（2）当动点P在第一象限时，在直线y=t（t<0）上存在点Q，满足以线段PQ为直径的圆过原点，且直线PQ与⊙O：x2+y2=3相切.求证：t是定值.

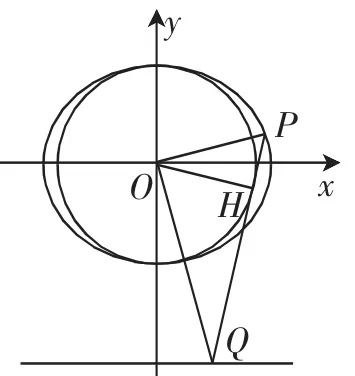
图1

（2）运用函数与方程思想去分析，可设P（x0，y0），Q（x1，t），其中3x02+4y02=12.这里引入了3个参数x0（y0），x1，t.由于点P与点Q是相关点，t是目标量，因此需要探求t与x0（y0），x1的关系式（方程组），然后通过解方程组使问题得到解决.

具体证法如下：由PQ·OH=OP·OQ及PQ2=OP2+OQ2，

联立①②消去x1，得

上面我们用函数与方程的思想方法，只设点的坐标，不设直线方程，通过研究目标变量与其他坐标变量的关系，很漂亮地解决了问题，比一般解法中设直线PQ及直线OQ的方程，然后用交轨法去求证t是定值要简单、直接.

有些直线与圆锥曲线的关系问题，设直线的方程往往很难解决，主要原因是运算太烦琐，但如果我们用函数与方程的思想方法去分析，却往往有意想不到的惊喜.下面我们再看一例.

图2

多么简洁巧妙的解法！本题如果按常规思路去设直线方程求解，其运算难度可想而知.下面我们再看一个练习.

练习：如图3，已知直线l过坐标原点，抛物线C的顶点在原点，焦点在x轴正半轴上.若点A（-1，0），B（0，8）关于l的对称点都在C上，求直线l和抛物线C的方程.

解析：本题的常规解法是设出直线l的方程y=kx（k>0），利用对称性条件求出B，A的对称点B再代入抛物线方程C：y2=2px（p>0），可求出k和p的值，解决问题，计算量不小.下面我们再试试用函数与方程思想来思考这个问题，其解法如下：

图3

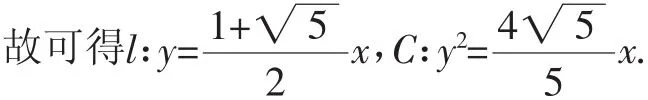
通过上面两个例子的分析，我们不难发现：由于直线和圆锥曲线都是用二元方程来刻画的，因此当我们设出点的坐标（参数），经过对条件的相应转换，列出相关参数的方程组，就可以通过解方程组使问题得到很好的解决.因此，函数与方程思想是研究和解决直线与圆锥曲线关系问题的重要工具.