高考中的立体几何问题研究

☉江苏省如皋市第一中学 邹小锋

立体几何是高中数学教学的重要组成部分，也是高考数学的热门考点，它对学生空间想象能力、逻辑思维能力、推理能力等具有较高的要求.通过对历年高考数学试题的统计不难看出，立体几何试题每年都会有，并且都是以解答题的形式出现，占据了较大的分值.因此，想要取得一个理想的高考数学成绩，研究高考中的立体几何试题非常必要.

一、立体几何知识概述

教材将高中数学立体几何部分分成了三个板块，分别是空间几何体、空间向量及空间中点、线、面之间的位置关系.通过这些知识的学习，能够发展学生的空间想象、逻辑思维、逻辑论证等方面的能力，是高中阶段数学教学的重要内容.高中数学新课程标准明确提出了立体几何对发展学生能力的重要意义，也提出了学生对立体几何学习的目标要求.高考不仅仅是选拔人才的重要考试，还是检验我们教学状况的重要工具，它可以直接反映出数学学科的课程教学内容和教学理念，它的题目设计直接影响着数学的教学.在历年的考试大纲中也对该部分知识提出了要求，但是还是有多数学生在这一部分的得分较低.这就说明，我们平时在该部分知识的数学教学还存在着一定的问题，还需要我们结合高考数学中该部分题目的情况去研究我们的教学.

二、高考数学立体几何部分问题分析

（一）高考立体几何部分问题概述

通过对近些年高考数学试题的分析统计可以看出，立体几何涉及的知识主要分为“了解”“理解”和“掌握”三个层次.其中需要掌握的知识有常见组合体的结构特征；证明空间位置关系的方法；空间向量的相关知识等，向量部分的知识是重中之重.在众多考题中，二面角是高考数学立体几何的常考点.

（二）高考数学常见问题分析

1.平行垂直类问题分析

平行垂直类问题提主要涉及线线平行垂直、线面平行垂直和面面平行垂直，它们之间的性质和定理可以构成如图1所示的关系图.在遇到问题的时候，学生就可以根据这一关系图（如图1），提取自己想要的知识点来解题.

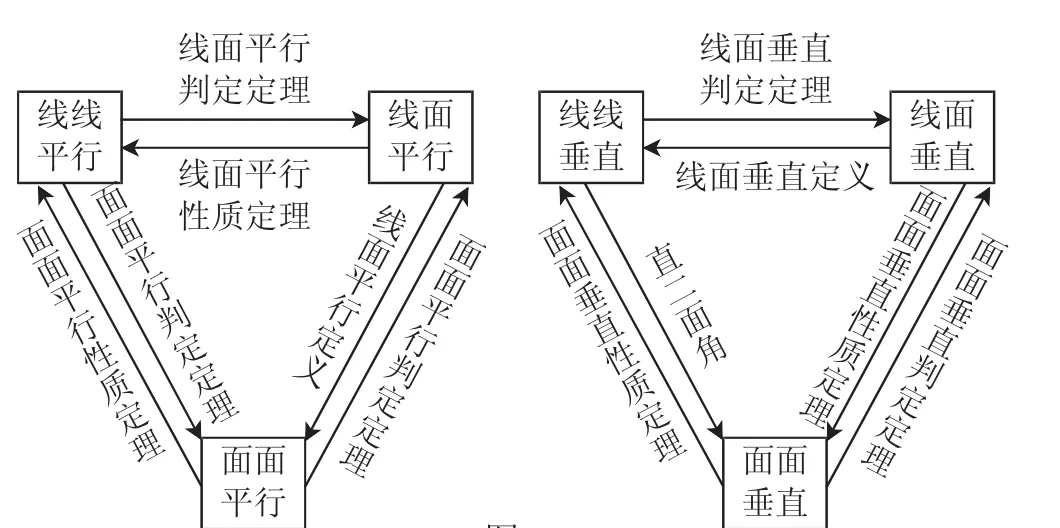
图1

在高考数学平行垂直类问题的证明中，不论是线线垂直（平行）或面面垂直（平行）通常选择向量法和综合法求解.

例1（2016年高考数学全国卷理科18）如图2所示，A，B，C，D，E，F为五面体的六个顶点，平面ABEF为正方形，AF=2FD，∠AFD=90°，二面角D-AF-E和二面角C-BE-F都是60°.

证明：平面ABEF⊥平面EFDC

分析：这道题考查的知识点较为全面，涉及了点、直线、平面之间的平行与垂直；直线与平面的数量关系等.与常见的立体几何问题相比，本题以不规则的三棱柱为载体，给学生的认知上提高了难度，但是在证明线面关系的垂直上较为直接，有助于学生的解答.在解决这一问题的时候，数形结合和转化的思想较为关键，线线、线面、面面之间的平行、垂直关系的转化应用广泛.

证法一：因为∠AFD=90°，所以AF⊥EF.

因为ABCD是正方形，所以AF⊥EF.

又因为DF∩EF=F，所以AF⊥面FEC.

因为AF⊂面ABFE，所以平面ABFE⊥平面EFDC.

证法二：在平面EFDC中过点D作DH垂直EF交EF于点H，令AF=4，DF=2.

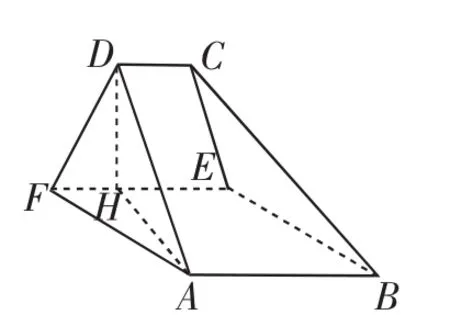
图2

因为AF⊥FD，AF⊥BF，所以∠DFE=60°.

那么DA2=DH2+AH2.所以DH⊥AH.

因为AH∩EF=H，所以DH⊥平面ABEF.

因为DH⊂平面EFDC，所以平面ABFE⊥平面EFDC.

解题误区：首先，有少数学生出现解题错误的原因是基础知识掌握得不够牢固，对相关的概念、定理不熟悉.例如，在题目中明确给出了条件“二面角D-AF-E和二面角C-BE-F都是60°”，但是他们就是找不准对应的角，他们想当然地认为二面角D-AF-E和二面角C-BE-F对应的角分别是∠DFE和∠CEF，最终求得DF=CE.

其次，部分学生选择了向量法来进行求解，导致在烦琐的计算面前出现计算错误.

第三，还有部分学生缺乏严谨的做题习惯，对题目中的坐标系图形化的歪歪斜斜，并且有的地方表述也较差，导致失分.

2.夹角类问题分析

在高考数学立体几何中，求夹角类问题主要有异面直线所成角、直线与平面所成角、二面角三种类型.在解决这类问题时，很多学生出现解题错误，主要的原因就是找不到要求的角，还有些是法向量求不出来.在解决求夹角类问题的时候，如果采用综合法来求解，关键是需要将两条异面直线通过平移等方法将它们放到一个平面上，然后通过所在三角形寻找解题突破口.另外，还可以通过在直线上找特殊点的方式和找平面角的方式来进行求解.不论是求异面直线的夹角还是直线与平面的夹角以及两个面的夹角，解题的关键就是将它们转变成同一个三角形内部的问题.如图3所示.

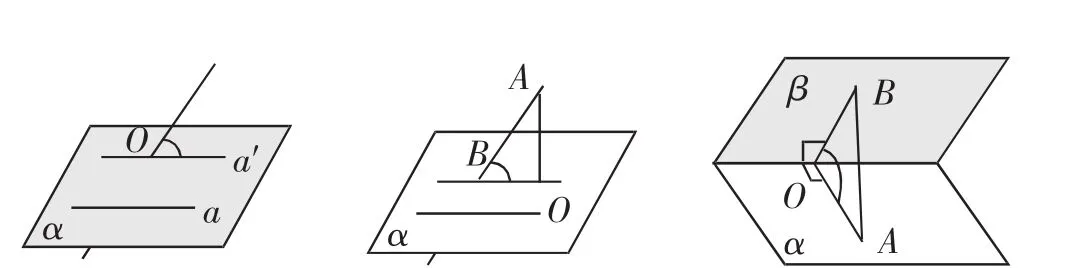
图3

在解决立体几何中的求角类问题时，不论是利用综合法还是向量法来求解，都是将角的问题转化为线线角的求解，学生可以根据自己的特长选择适当的方法来求解.

例2 如图4所示，四边形ABCD是菱形，∠ABC=120°，E，F是平面ABCD同一侧的两个点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.求直线AE与直线CF所成角的余弦值.

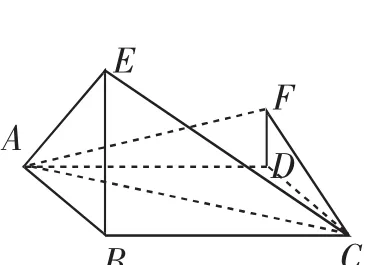
图4

分析：本题相对较为传统，是学生较为常见的菱形，但是，又在菱形的基础上进行了创新.题目中要求异面直线所成角，通过向量法和综合法都可以完成解题.

解法一：如图5，作AM∥DF，并且AM=DF，连接BM交AE于点N，那么BM∥CF且BM=CF，这样就AE和CF所成角就转化为AE和BM所成角.cos∠ENB=（.△AMN和△EBN相似，那么BN=2NM.又BM=CF=∠ENB=∠AEB）

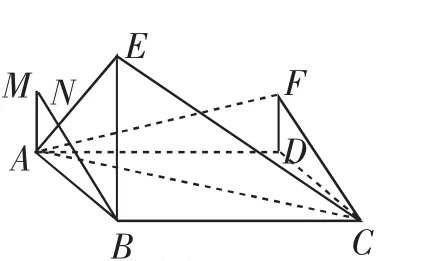
图5

解法二：以G—→B和GC所在方向为x轴和y轴，以GB为单位长度建立空间直角坐标系，如图6.

图6

解题误区：首先，部分学生存在审题不清的情况，题目中明确说明ABCD是菱形，他们却将它当成正方形，将AB和BC看成垂直，并在它们上边来建立直角坐标系.有的即使坐标系构建正确，但是计算能力较差，导致cos〈〉计算错误.其次，部分学生解题过程不够严谨，忽视了异面直成了最终答案.还有部分学生在证明平面ABC⊥平面AFC的时候，直接由显现垂直（EG⊥AC和EG⊥FG）得出来，并没有经过线面垂直（EG⊥平面AFC）的过渡.

纵观近些年高考数学立体几何部分的问题不难发现，该部分知识以基础知识为依托，主要考查学生的数学思想和解题技能.另外，运算能力也是学生应对立体几何问题的必备素质.因此，在平时的数学教学中，要注重学生这些方面能力的培养，提高学生解决立体几何问题的能力，进而提高高考数学成绩.H