突破失误,分析对策
——以2018年全国Ⅰ卷理科第19题为例
☉广西桂林市宝贤中学 佟 震
2018年高考已经结束,通过对高考试题进行深入分析与研究,进行读题、做题、议题、思题等步骤,关注高考对数学教学的指导思想,让人感想颇多.下面以2018年全国Ⅰ卷理科第19题为例,这是一道以椭圆为背景的解析几何试题,表述清晰,难度中等.而从高考后对此题的作答调查情况来看,仍有颇多的典型失误.
一、试题呈现
(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB.
本题涉及椭圆的标准方程与几何性质,直线与椭圆的位置关系,直线的方程与斜率等基础知识,考查函数与方程思想、数形结合思想、化归与转化思想,以及分析问题的能力和运算求解能力等.
解析:(1)由已知得F(1,0),l的方程为x=1.
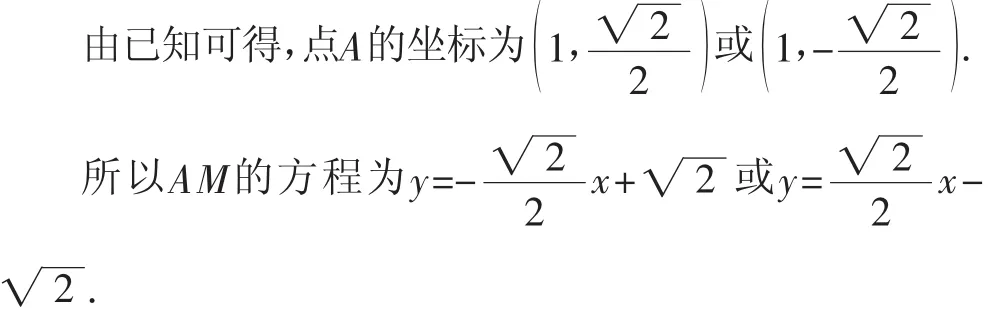
(2)当l与x轴重合时,∠OMA=∠OMB=0°.
当l与x轴垂直时,OM为AB的垂直平分线,所以∠OMA=∠OMB.


从而kMA+kMB=0,故MA,MB的倾斜角互补.
所以∠OMA=∠OMB.
综上,∠OMA=∠OMB.
二、典型失误与对策分析
1.会而不全
在第(2)问的证明过程中,没有分“l与x轴重合”“l与x轴垂直”和“l与x轴不重合也不垂直”进行分类讨论,直接设出直线l的方程为y=k(x-1),再加以推演与证明.
分析:这是解析几何中涉及直线方程的斜率存在性问题的最常见的典型失误,属于逻辑性错误.这类典型失误在平时课堂教学过程中经常会加以强调.而在实际解答过程中,由于受到问题的特殊状态、高考状态下学生思维的片面性等的影响,导致此类失误一再出现.
对策:加强数学思维的训练,特别是严谨性训练.逻辑推理与解答过程是类似的,必须具备等价性.而在解答题的书写过程中,就必须严谨,正确分清从一般到特殊,从特殊到一般的关系.在以上典型失误中,解答过程中画出的直线l是某一瞬间的、特别的情况,不可能同时包括“l与x轴重合”“l与x轴垂直”和“l与x轴不重合也不垂直”这三种情况,进而在书写解答的过程中就导致遗漏,造成会而不全.
在教学过程中,必须重视对学生数学思维的发散性(变式法)、灵活性(多视角)、创新性(构造法)及全面性(等价转化)的培养与训练.针对具体的数学问题,引导学生从问题的不同角度、各种关系、相关属性等进行全面考虑,多视角灵活地解决问题.
2.运算不准
在第(2)问的证明过程中考查数学基本运算,包括直线的斜率之和,直线与椭圆的位置关系等问题中的运算,有的在kMA+kMB的转化过程中运算出错,有的在直线方程代入椭圆方程中运算出错,有的在利用根与系数的关系转化中运算出错,运算过程中变量较多,运算繁杂,从而导致失误.
分析:运算错误分析其原因有两个:一个是知识性错误,一个是心理性错误.
(1)基本知识掌握不牢固,导致知识性错误.本题比较常见的有直线的斜率公式出错,直线方程的设置与代入过程中的运算出错,直线与椭圆的位置关系中联立方程组的运算出错,根与系数的关系中表达式的运算出错等.而在其他相关数学知识中,也经常会由于相应基本知识的掌握情况不好而导致运算错误的.
(2)心理因素导致麻痹大意或过度紧张.由于在高考的高压状态下,容易分为两个极端,一个是麻痹大意,一个是过度紧张,其都是心理因素不稳定而造成.而其最终造成的结果就是要么简单运算不够重视,要么心态不稳导致笔误等,都会造成运算错误.
对策:加强课内、课外训练.
(1)课内强化训练.在课堂教学中,重视对基本运算求解能力的训练,力求做到基本运算零失误.在专心、细心、耐心、信心等方面下功夫,从学生的每一个细节上寻求突破,全面提升.
(2)课外面批训练.利用自习课等,在作业解答、测试训练中,通过课外面批,针对出现的错误,指导学生有针对性地从知识点、心理素质等加以训练,促进学生基本知识的进一步熟练掌握,心理素质的进一步提升.
3.思维不畅
在第(2)问的证明过程中,当l与x轴不重合也不垂直时,要证明∠OMA=∠OMB成立,转化为MA,MB的倾斜角互补,即kMA+kMB=0来处理.由于思维不畅,无法进行上述的合理转化,导致无从下手.
分析:解决问题的思维方式往往是巧妙转化与化归,解题思维的切入点是解决问题的关系.通过分类讨论,当l与x轴重合时,∠OMA=∠OMB=0°;当l与x轴垂直时,OM为AB的垂直平分线,所以∠OMA=∠OMB;而当l与x轴不重合也不垂直时,如何选定证明∠OMA=∠OMB时的切入角度,就是解决问题的关键.
(1)思维不畅的一个主要原因是知识点之间的联系不密切.很多的数学知识点之间是相互联系,密切相通的,这在解题过程中经常会加以思维转化.例如直线与圆锥曲线有交点时对应的判别式的正负取值的不等式,直线的斜率与对应的倾斜角,直线垂直与圆的关系,平面向量的数量积与垂直、平行关系等,都是思维转化的一个重要知识点.
(2)思维不畅的另一个原因就是缺少解题的灵活性,当一种思维不畅时,可以采取其他思维方法来转化与应用.其实本题中,当l与x轴不重合也不垂直时,要证明∠OMA=∠OMB成立,还可以转化为:①结合点F到直线AM、AN的距离相等,利用角平分线的性质来解决;②结合点B关于x轴的对称点B′在直线AM上,利用对称法来解决;③通过Rt△BEM∽Rt△ADM的转化来证明对应的线段成比例,利用几何法来解决;④通过∠OMA=∠OMB,利用向量法来解决等.
对策:加强全面分析和一题多解的训练.
(1)加强全面分析.在分析问题时,要全面把握题目所提供的关键信息,寻找相关之间的关联,探索已知信息与所求结论之间的关联通道与转化途径,力求解题方向明确,思维体系通畅,内在联系明了,解题运算简单.
(2)加强一题多解的训练.在传统的教学过程中,学生的思维极具定向性、专一性.而“一题多解”恰好是克服其思维定式的有效途径,同时培养学生发散思维和思维灵活多样性的有效方法.通过“一题多解”的训练,培养学生从多角度、多途径、多知识寻求解决问题的方法,开拓解题思路,进而通过多种解法的对比与分析中选取最佳解法,总结解题规律,提升解题能力,增强思维品质,进而提升数学核心素养.
三、几点反思
以上只是这道解析几何试题的一些典型失误,在其他知识点的解题中也存在类似的失误,有时还有其他方面的失误.这些典型失误在平时教学过程中重复出现,而在考场中也时时重演着.
从教师层面,加强与学生面对面的交流,指导学生从平时抓起,从“纠错本”入手,注意细节,提高效益.不少教师对学生学习方式、学习方法方面的指导还不够,沿用传统的线性方式记笔记和订正错题,没有形成体系化,导致记忆效果不佳.
从学生层面,必须加强学科学习体系、学习方式、学习方法等方面的改进,注重自主学习,使得学科内容体系化、解题过程严谨化、学习动力内驱化,真正做到自主学习,科学掌握.
总之,教师要充分挖掘学生自身内部的能动力,引导学生自主学习,减少或避免由于各种原因导致的典型错误,真正达到学会、会做、做好的目的.W

