斯托克斯矢量和穆勒矩阵在偏振光中的应用研究
何启浩
(西南民族大学电气信息工程学院,四川 成都 610041)
1941年物理学家琼斯(R.C.Jones)提出了用一个2×1列矩阵来表述一任意完全偏振光的光矢量的两个分量,该列矩阵也称为琼斯矢量.一光学元件(偏振器等)可用一个2×2矩阵(称为琼斯矩阵)来表述.用琼斯矩阵来表述光波的任意偏振态及其变换与叠加,可以比较方便地计算得出任意完全偏振光通过不同组合的偏振光学器件后出射光的各种偏振态[1-5}.但是,对于自然光和部分偏振光却不能用琼斯矩阵(矢量)来表述,这样琼斯矢量和琼斯矩阵的应用受到一定的限制.物理学家斯托克斯(G.G.Stokes)提出了一束光波的强度和偏振态可用四个参量(称为斯托克斯参量)来表述[6-7],对于完全偏振光,自然光和部分偏振光都可以用斯托克斯参量(也称斯托克斯矢量)来表述.物理学家穆勒(Mueller)提出可用一个4×4矩阵来表述一光学元件(偏振器等)[6-7],该矩阵也称为穆勒矩阵.
1 完全偏振光和自然光部分偏振光的斯托克斯矢量表示方法
物理学家斯托克斯提出一束光波的偏振态和强度可用4个参量来表述,这4个参量构成一个四维矢量S(称为斯托克斯矢量)[6-7],
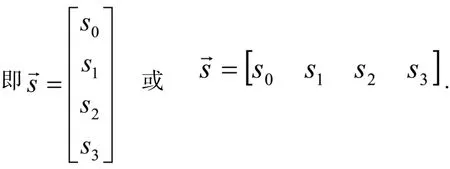
与琼斯矢量不同,斯托克斯四个参量(矢量)都是光强的时间平均值,可以完全确定任意完全偏振光、自然光和部分偏振光.
1.1 完全偏振光的归一化斯托克斯矢量
线偏振光[6-7]:水平方向[1 1 0 0];垂直方向[1 -1 0 0];±45°方向[1 0 ±1 0]; 一般 [1 cos2α sin2α 0].
圆偏振光[6-7]:右旋圆偏振光[1 0 0 1];左旋圆偏振光[1 0 0 -1].
1.2 自然光和部分偏振光的归一化斯托克斯矢量
自然光 [1 0 0 0][6-7].
部分偏振光:水平方向占优[2 1 0 0];垂直方向占优[2 -1 0 0];±45°方向占优[2 0 ±1 0];一般[2 cos2α sin2α 0].
琼斯矢量是二维矢量,而斯托克斯矢量是四维矢量,在运算方面虽然使用琼斯矢量方便一些,但是琼斯矢量仅能表述完全偏振光:而任意完全偏振光,自然光和部分偏振光都能用斯托克斯矢量表述,这样,使用斯托克斯矢量运算更全面一些.这正是斯托克斯矢量表示方法的特点.
2 偏振光学器件的穆勒矩阵表示方法
物理学家穆勒(Mueller)提出偏振光学器件可由
4×4矩阵M来表述,每一种偏振器对偏振光的变换特性都可用一个穆勒矩阵来表示.
2.1 线偏振器和1/4波片的穆勒矩阵[6-7]
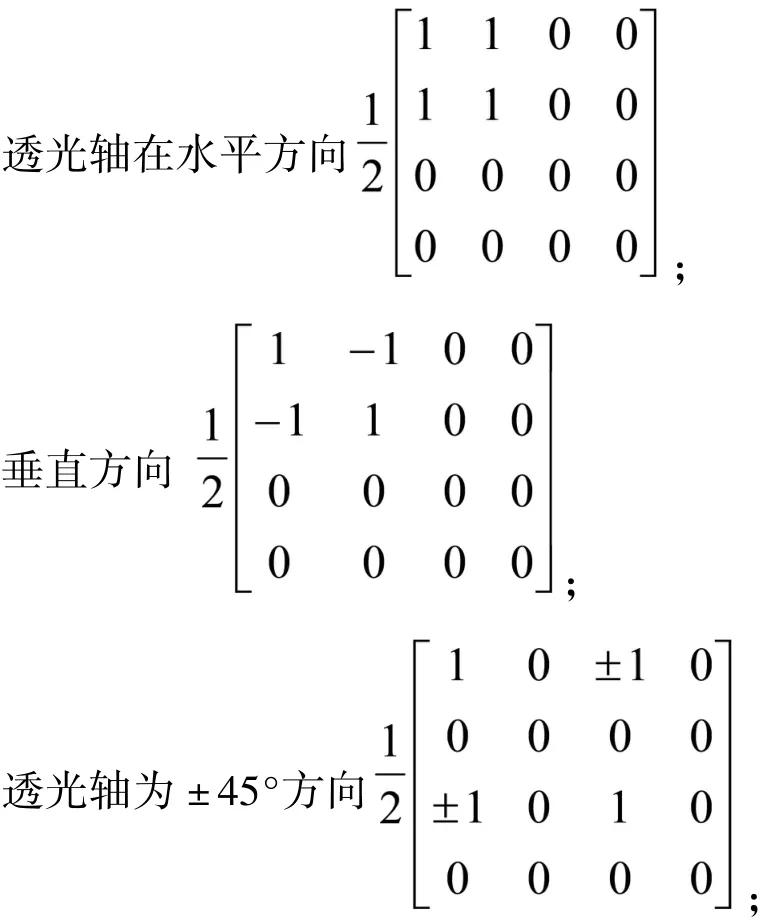
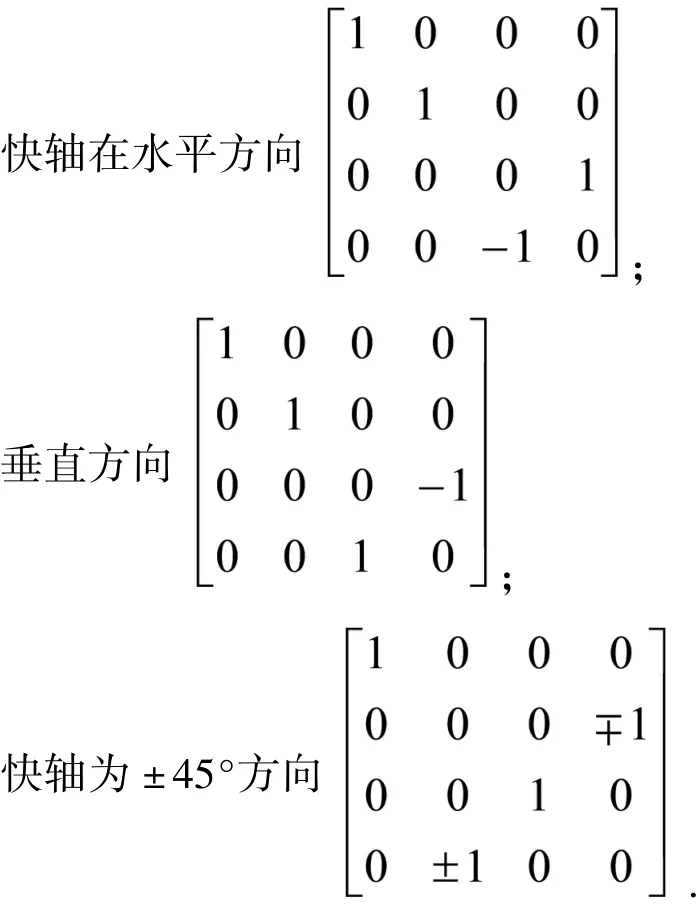
2.2 圆偏振器的穆勒矩阵
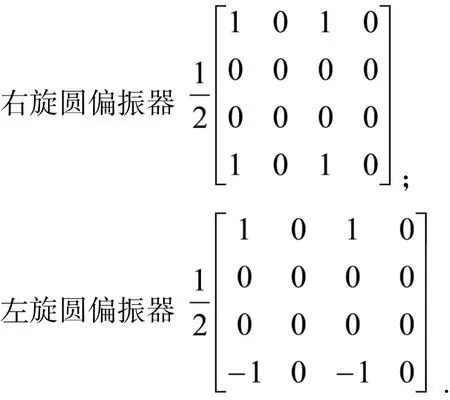
3 斯托克斯矢量和穆勒矩阵的应用实例
3.1 斯托克斯矢量的应用
由于斯托克斯矢量可以表示为4X1的列矩阵或1X4的行矩阵,它在描述完全偏振光,自然光和部分偏振光比较方便.例如,部分偏振光可由自然光叠加某方向振动占优的线偏振光而合成.这样,水平方向占优的部分偏振光的斯托克斯矢量可由自然光和水平方向的线偏振光的斯托克斯矢量相叠加而合成(见(1)式);45°方向占优的部分偏振光的斯托克斯矢量可由自然光和45°方向线偏振光的斯托克斯矢量相叠加而合成(见(2)式).垂直方向占优的部分偏振光和一般的部分偏振光的斯托克斯矢量叠加方法与上述一样(见 1.2).
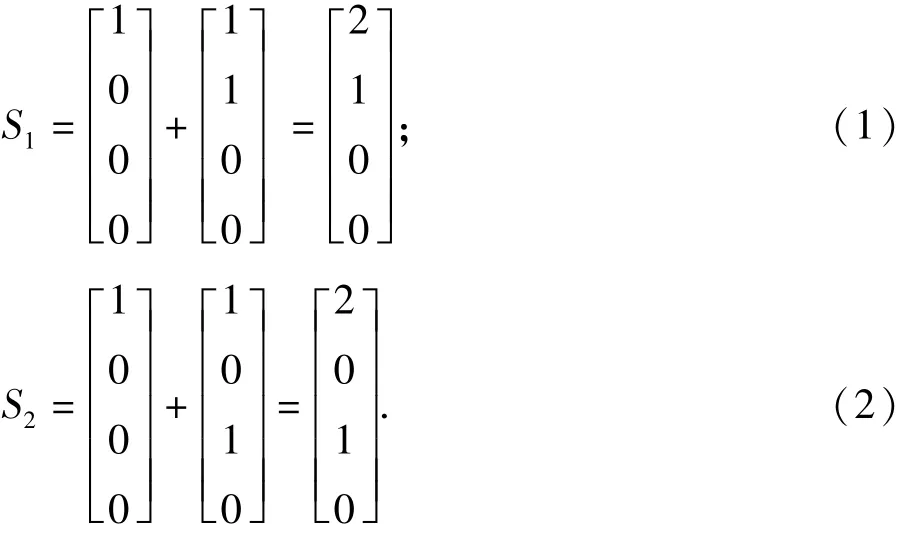
3.2 穆勒矩阵的应用
一束自然光先后通过一个透光轴为45°线偏振器和一个快轴在垂直方向的1/4波片,则:
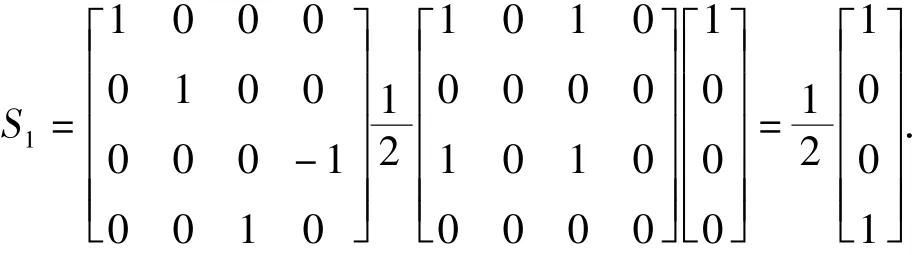
为一强度减半的右旋圆偏振光;而
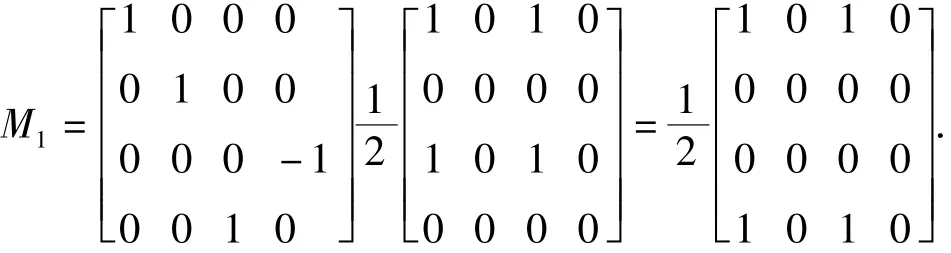
为右旋圆偏振器的穆勒矩阵(见2.2).
一束水平方向占优的部分偏振光相继通过一个透光轴为水平方向的线偏振器、一个快轴沿45°方向的1/4波片和一个左旋圆偏振器,出射光为:即出射光为强度为3/4的左旋圆偏振光.
一束右旋圆偏光相继通过一个透光轴为垂直方向的线偏振器;一个快轴与x轴夹—45°的1/4波片;一个透光轴与x轴夹—45°的线偏振器;一个90o的右旋圆延迟器[7],出射光为:
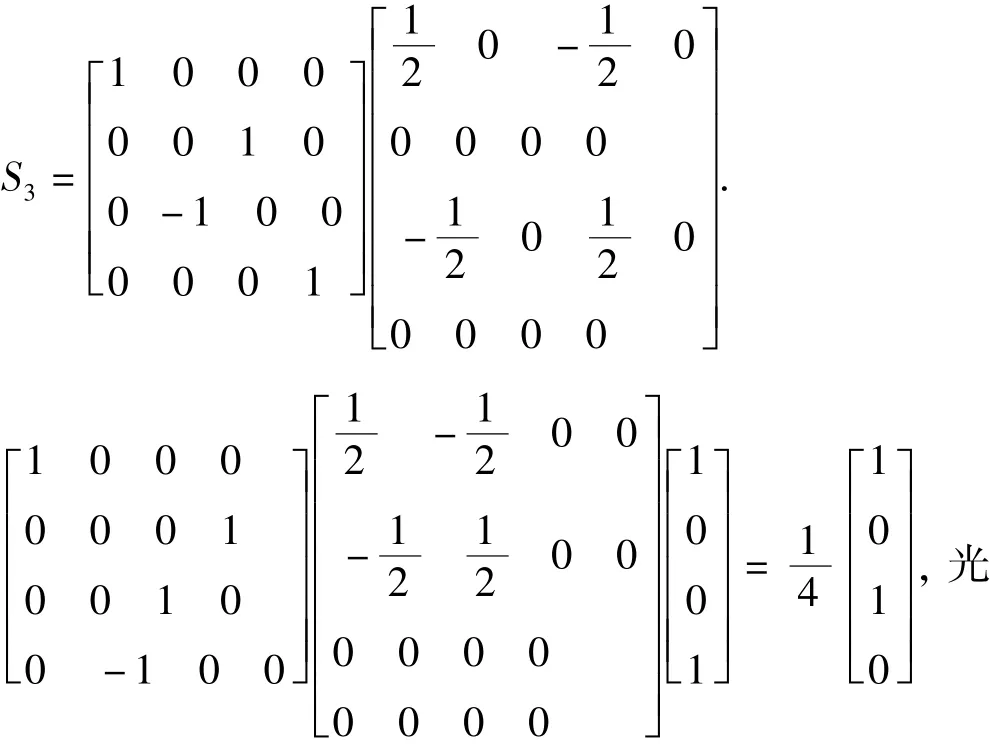
强为1/4与x轴夹45°的线偏振光.
4 完全偏振光的斯托克斯矢量与琼斯矢量的变换关系
设一个完全偏振光为:
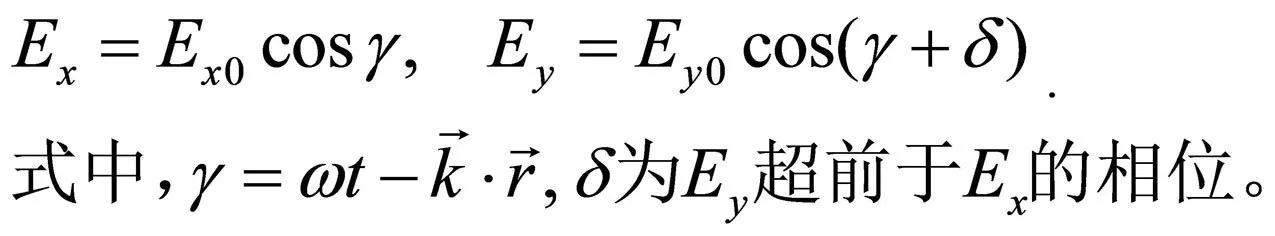
它的斯托克斯矢量为:
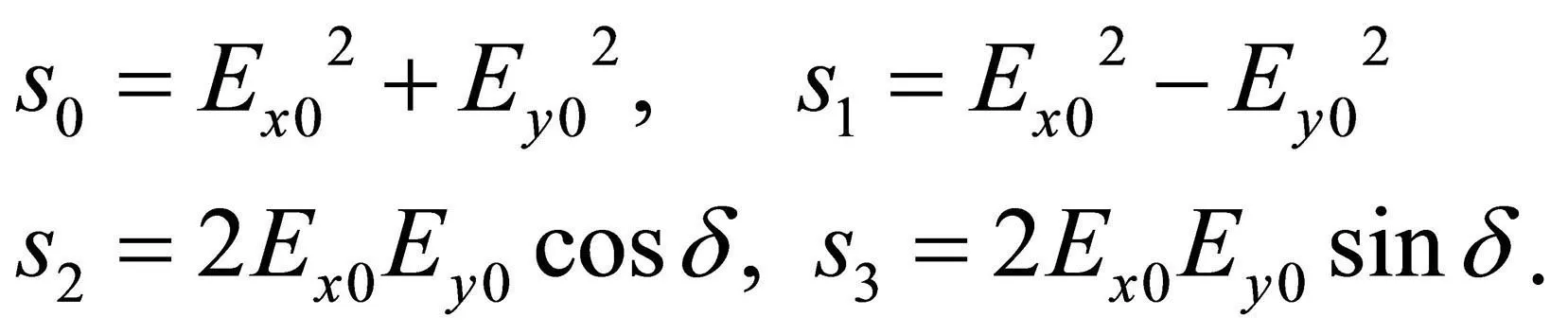
它的琼斯矢量可写为:
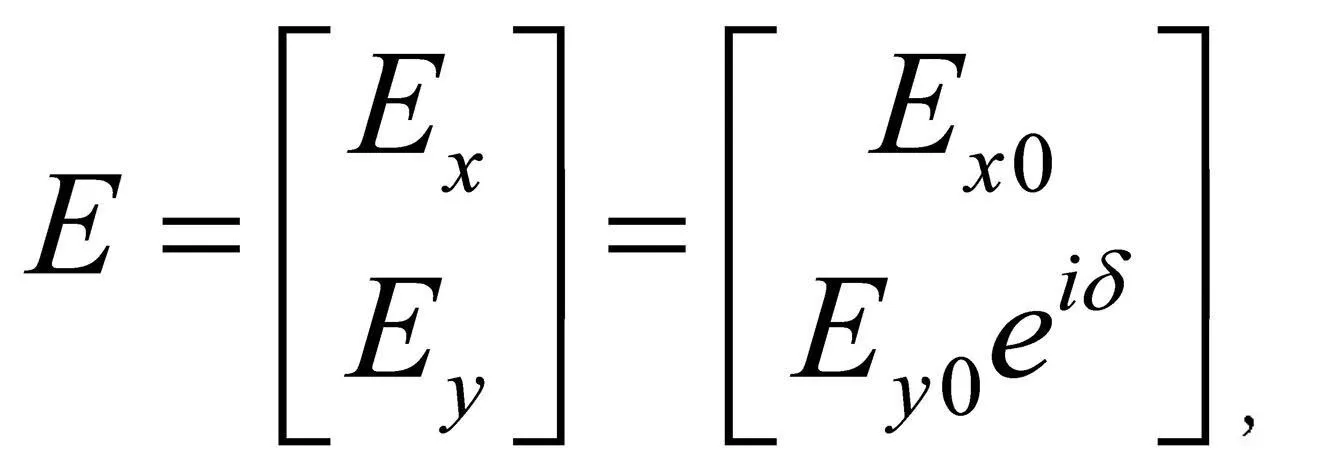
其琼斯矢量的共轭矢量为:
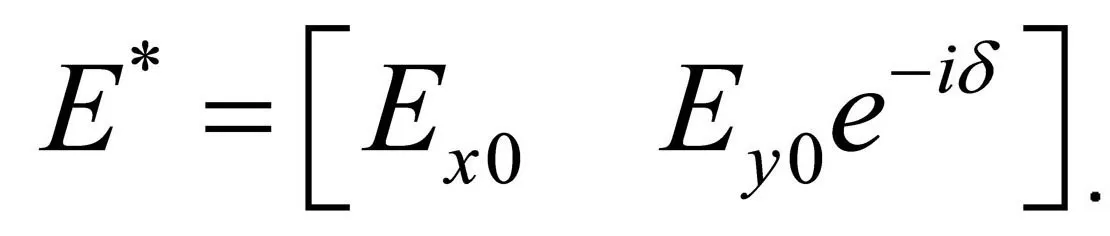
为了变换计算方便,引入四个矩阵(叫做夹心矩阵)[6],
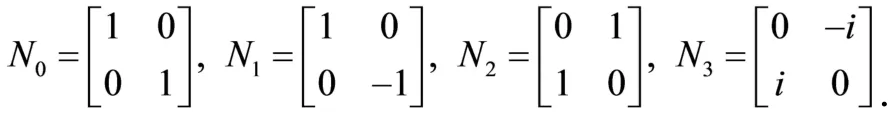
则,这四个斯托克斯参量与琼斯矢量的关系可以表示为:
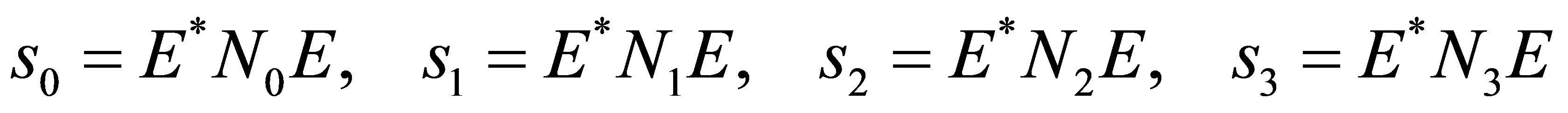
用下例来验证上面的变换关系式:
一束左旋圆偏振光,其琼斯矢量[8-14]和其共轭矢量为:;则左旋圆偏振光的斯托克斯参量分别为:
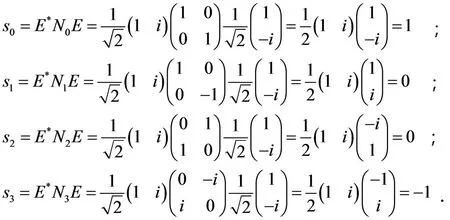
5 结束语
光的各种偏振态使光增加了一个可被调控的自由度和信息.可以通过叠加两个及以上适当的偏振光以及适当的组合各种偏振光学器件与光路设计,可进一步按设计的要求去改变光的偏振态.因此,不同偏振光的叠加的计算,以及计算光通过不同的偏振光学器件后的偏振态是应用中的一个重要的前题.琼斯矢量是二维矢量,而斯托克斯矢量是四维矢量,在运算方面使用琼斯矢量便利一些.但是琼斯矢量只能表述完全偏振光,而斯托克斯矢量对于完全偏振光、自然光和部分偏振光都能表述.使用斯托克斯矢量运算更全面,这是斯托克斯矢量表示方法的特点和优点.对于计算自然光、部分偏振光和不同完全偏振光的叠加与变换时,以及计算自然光、部分偏振光和不同完全偏振光通过由不同偏振光学器件组成的复杂系统后出射光的偏振态时,笔者认为可以先运用斯托克斯矢量表示法计算,再运用琼斯矩阵(矢量)计算,这样既可以处理自然光、部分偏振光和各种完全偏振光,又在计算方面便利一些.当然,这涉及到斯托克斯矢量与琼斯矢量的变换运算,本文只讨论了由琼斯矢量变换到斯托克斯矢量的方法,而由斯托克斯矢量变换到琼斯矢量的方法有待于进一步的探讨和研究.

