关于一类具有负系数的广义单叶函数性质
何 涛,周海燕,李书海
(赤峰学院数学与统计学院,内蒙古 赤峰 024000)
1 引言
设函数 f(z) 和g(z) 在D = {z:z<1}内解析,如果存在解析函数w(z)满足w(0)=0,w(z) <1,使得f(z) = g(w(z)) ,则称 f(z) 从属于 g(z) ,记为 f(z) ≺ g (z)[1].

用S(a,k)表示在单位圆盘D内具有如下形式的解析单叶函数全体函数组成的类.令Ta,k()表示Sa,k()中的具有负系数单叶函数的子类:

显然T(1,2)=T[2].Vinod Kumar在文献[2]中引进并研究了T的特殊子类:
定义A 设A,B∈R, -1≤B <A≤1.函数f(z) ∈T属于函数类P(A,B) 当且仅当

文献[2]中讨论函数类P(A,B)的几何特征,先证明函数类充分条件,得到类中函数的系数不等式、偏差、覆盖、闭包定理和极值点等性质.国内外学者在文献[3-17]中分别研究了T的不同子类几何函数性质,得到重要结果.
以下,在Sa,k()上引进广义解析函数类,首先给出积分表达式、充分条件,由此得到类中函数的系数不等式、偏差、覆盖、闭包定理和极值点等性质,所得结果推广了文献[2]中的主要结果.最后还进一步讨论函数类的Hadamard卷积的封闭性质和包含关系,得到新结果.
2 定义及有关引理
首先引进函数类:
定义1 设A,B∈R,a >0, A≤1, B ≤1,A≠B,0≤λ ≤1.函数f(z) ∈S(a,k)属于函数类Pk(a,λ,A,B)当且仅当

令
TPk(a,λ,A,B)=Ta,k()∩Pk(a,λ,A,B).
显然,定义中分别取 a = 1, -1≤B < A≤1,λ = 1 时,P2(1,1,A,B) 和TP2(1,1,A,B) 为文献[2]中研究的函数类.
引理1 函数fz()∈Pk(a,λ,A,B)当且仅当

证明:根据从属关系的定义,f(z)∈Pk(a,λ,A,B) 当且仅当在D中存在解析函数w(z)满足w(0)=0,w(z) <1,使得(4)式等价于(3)式.证毕.

3 主要结果及其证明
下文中,如无特殊说明,参数k,A,B,a均满足条件:
k,A,B ∈ R,k≥2,a > 0, A≤1, B≤1,A ≠ B,0 ≤λ ≤1.
定理1 函数 f∈ Pk(a,λ,A,B) (0 < λ < 1) 当且仅当

其中解析函数w(z)满足w(0)=0,w(z)<1,C为任意常数.
证明:设f∈Pk(a,λ,A,B) (0< λ <1) ,根据从属关系定义可知,存在解析函数类w(0)=0,w(z)<1使得:
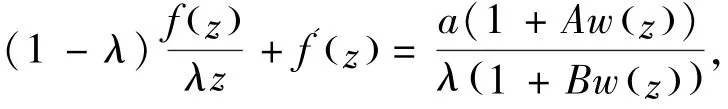
由一阶非齐次微分方程的求解公式可得
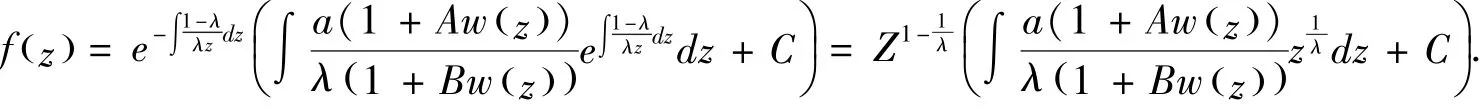
上述证明是可逆的.故函数f∈Pk(a,λ,A,B)当且仅当(5)式成立.
其次,给出系数不等式:
定理2 设函数 f(z) ∈ S(a,k) ,若满足条件

则f(z)∈Pk(a,λ,A,B).
证明:设不等式(6)成立.令 z = 1 ,由 f(z) ∈ Tk(a) 和利用(6)得到

因此,利用最大模原理,可得

由引理1可知fz()∈S∗k(a,A,B) .
定理3 设函数 f(z) ∈ T(a,k) ,则
①当-1≤B<A≤1,B≤0时fz()∈TPk(a,λ,A,B)的充要条件为

②当-1≤A<B≤1,B≥0时fz()∈TPk(a,λ,A,B)的充要条件为

证明:因 TPk(a,λ,A,B) ⊂ Pk(a,λ,A,B) ,所以由定理2 可知,定理3 的充分性显然成立 . 只需证明必要性即可.先证明①的必要性.
设fz()∈TPk(a,λ,A,B),由引理1得到
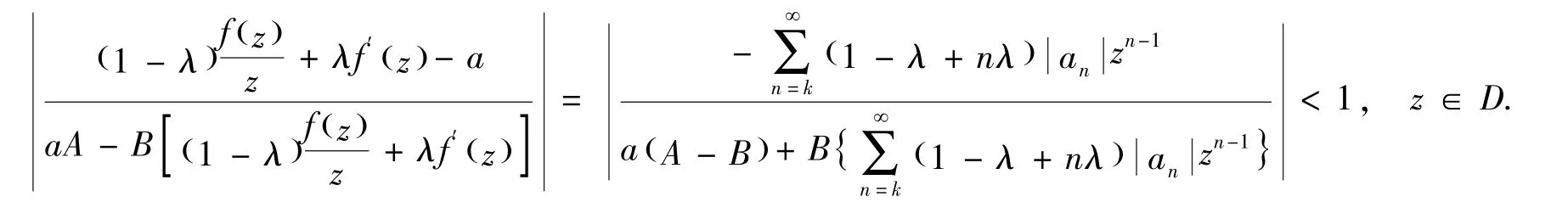
由于对于任意复数z,满足的 Rez≤z,所以

使用z→1-时,从(9)可得到 (7)式.
用相同的方法容易(8)成立.如果取函数
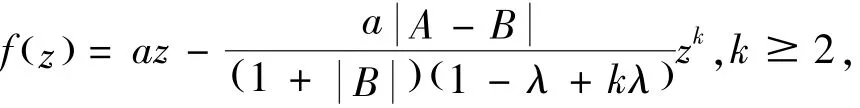
则(7)和(8)式均能达到准确值.证毕.
下面利用系数不等式讨论函数类TPk(a,λ,A,B)的基本性质.
定理4 若 f∈ TPk(a,λ,A,B) , z= r,则①当 - 1≤B < A≤1,B ≤0时,有

证明:①设 f∈ TPk(a,A,B) ,由定理 3 中①可知

因此

从而①成立.用相同的方法证明②.证毕.
定理5 设函数f(z)∈TPk(a,λ,A,B ),则函数

也属于函数类 TPk(a,λ,A,B ).
证明:由(10)式,得到

因f(z)∈TPk(a,λ,A,B ),分两种证明.当 -1≤B <A≤1,B≤0时利用定理3中①可知

由定理3推出,F(z)∈TPk(a,λ,A,B ).同理,当 -1≤A<B≤1,B≥0时,利用定理3中②容易证明F(z)∈TPk(a,λ,A,B).证毕.
定理6 设c是实数且c> -1,k≥2,又设F(z)∈TPk(a,λ,A,B ),则(10)式定义的函数f(z),在z<R∗是单叶的,其中

证明:设

由(10)式,得到

要得到结果,只要在 z ≤R∗时,需满足条件f′(z)-a<a或

如果
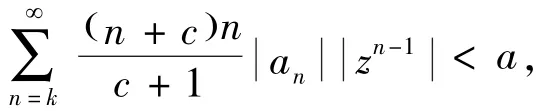
则有 f'(z) - a < a,而有定理3,得
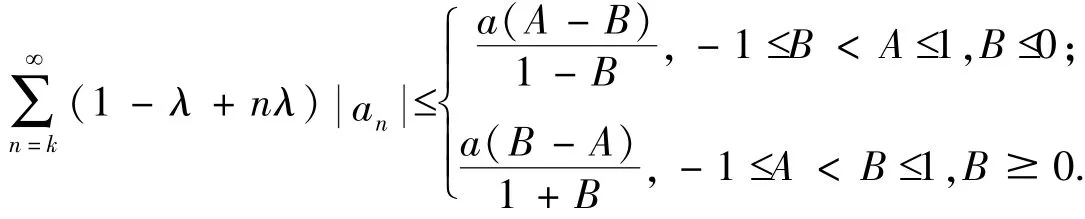
因此,如果

或者
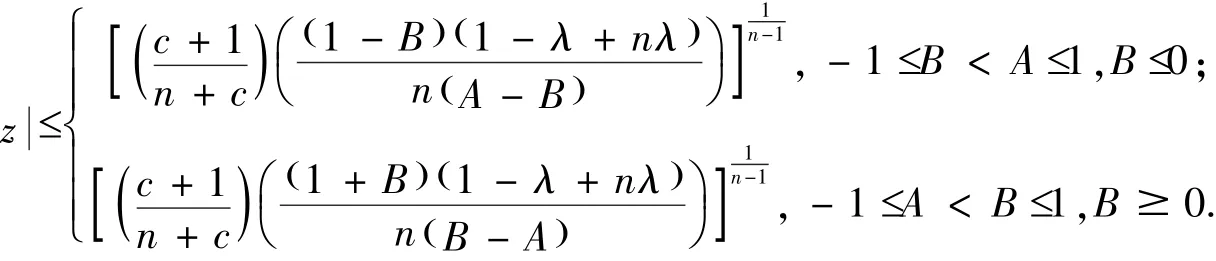
(10)式将满足,f(z)在z<R∗为单叶函数.
如果取函数

就能达到准确值.证毕.
定理7 设k∈R,k≥2,a >0,如果函数

属于类 TPk(a,λ,A,B) ,则当,函数 h(z) =也属于 TPk(a,λ,A,B) 类.
证明:由于f( z)∈TPk(a,λ,A,B) ,由定理3可得到

因此

由定理3 推出 h(z) ∈ TPk(a,λ,A,B) . 证毕.
定理8 设

则函数 f∈ TPk(a,λ,A,B) 的充要条件为

证明:(充分性):设
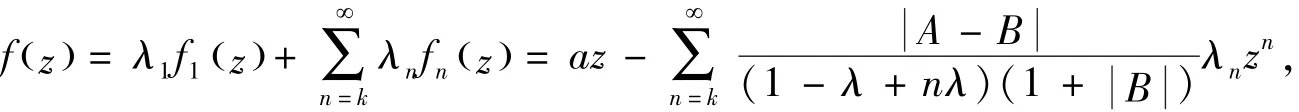
因此
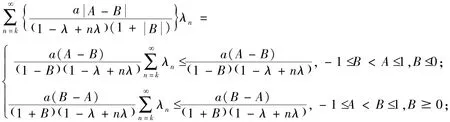
因此由定理3 可知 f∈ TPk(a,λ,A,B) .
(必要性):设 f∈ TPk(a,A,B) ,由定理3 推出

设

因此

证毕.
注:定理3-定理8中分别取a=1,-1≤B <A≤1,λ =1,时.就得到文献[2]中的全部结果.
最后,讨论类中函数的Hadamard卷积的封闭性和包含关系.
设 fi(z) =∈ T(a,k) (i = 1,2) 则函数 f1(z) 和 f2(z) 的 Hadamard 卷积定义为:

定理9 设

若 A-B ≤(1- λ +kλ) (1 + B ),则 ( f1∗ f2)(z) ∈ TPk(a,A,B) .
证明:因为fi(z)∈TPk(a,λ,A,B)(i=1,2) ,由定理3可得到
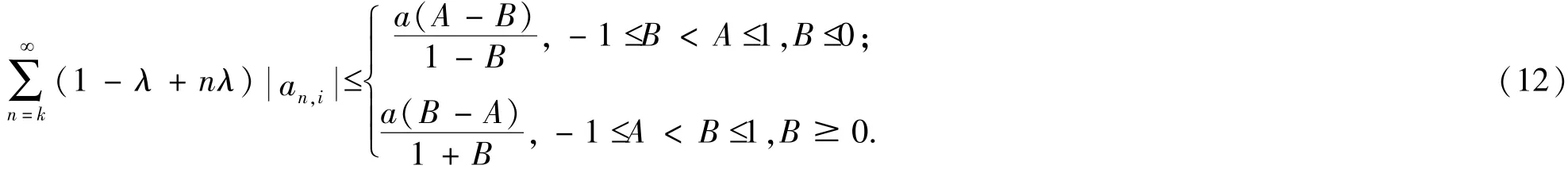
要证明 ( f1∗ f2)(z) ∈ TPk(a,λ,A,B) , 只需证明

利用Cauchy-Schwarz不等式,从(12)得到

即(13)式成立.证毕.
定理10 设0 ≤λ1≤λ2≤1 ,则

证明:设fz()∈TPk(a,λ2,A,B),分两种证明.
当 -1≤B <A≤1,B≤0时,利用定理3中①可得
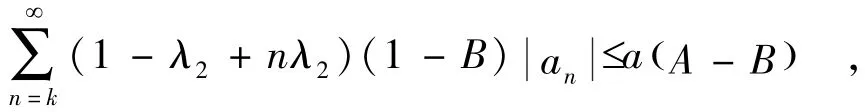
由于λ1≤λ2,且1-λ+nλ为关于λ的增函数,则有

即fz()∈TPk(a,λ1,A,B),(15)式可证.同理,当-1≤A<B≤1,B≥0时,利用定理3中②容易证明TPk(a,λ1,A,B) ⊆ TPk(a,λ2,A,B) . 证毕 .
4 小结
首先,利用从属关系和微分方程方法讨论了该类TPk(a,A,B)中函数的积分表达式和系数不等式,其次,研究其几何特征和极值问题,得到较广义的结果推广相关结论.该类函数中还有优化问题、对数系数以及映射区域面积等有很多待进一步研究的有趣问题,需要我们深入探究.

