各向异性粘弹流体材料拉伸流动研究
付 强
(西南民族大学期刊社,四川 成都 610041)
在流变学和非牛顿流体力学研究中,首先发展起来的是关于测粘流动研究,这是与各类粘度计的研制和应用密切相关[1].近几十年以来,拉伸流动的研究得到迅速发展,这是因为拉伸流动不仅对高聚物加工有重要意义[2-5],而且这一类流动也存在于其他有实际意义的过程中.在高聚物生产中,有一系列工艺过程,可归结为以拉伸为主的流动典型的过程有高分子熔体纺丝、管状薄膜吹塑和熔体压延等(如图1示).由于这一类流动的实际意义较大,因而在流变学和非牛顿流体力学中,十分重视对粘弹流体拉伸流动的研究[6].
高分子液晶与小分子液晶在动力学性质上有很大差异,而静力学性质基本相同.
液晶高分子材料是典型的各向异性材料,具有各种特殊性能的功能材料[7-14],工农业生产中有非常重要的应用.

图1 高分子熔体纺丝示意图Fig.1 schematic diagram of polymer melt spinning
1 拉伸粘度
拉伸粘度就是流体材料从管道中流出,垂直于流动方向的流体材料横断面积上所承受的拉应力与拉伸应变速率的比值[15].
简单流体的本构方程[16-22],可以写为以下形式:

根据物质客观性原理,应当满足:

同时,C =QC QT,C保持不变,因此:

所以有:

对于拉伸流动,偏应力张量具有以下形式:

对于简单流体,本构方程:简单流体的本构方程,可以写为以下形式:

可以定义下述拉伸流体物质函数:

拉伸粘度可由下式定义(k为主拉伸方向的拉伸率):

2 纺丝拉伸流动
设纺丝拉伸流动的速度场:

这里把上式代入式 x1= ξ1,x2= ξ2,x3= ξ3


因此,

整理得:

即

则

整理得:

设剪切速率为:

代入式(7.92)得:设剪切速率为:

代入得:

其中剪切速率:
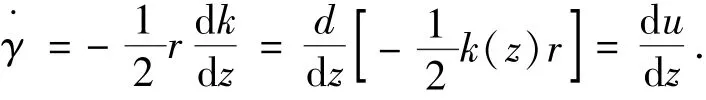
这表明剪切运动在垂直于拉伸轴(z轴)的方向.
由于拉伸粘度定义为:

所以纺丝拉伸粘度为:

两端同除以零剪切粘度(η0)得:

3 结论与讨论
图2(a,b)在不同拉伸速率下无量纲化拉伸粘度随剪切速率的变化曲线;说明ηe/η0=3是一个重要关键数字,即拉伸粘度是剪切粘度的3倍时,材料的流动性能和牛顿流体一致;当ηe/η0小于3时,剪切速率于拉伸粘度成反比;当ηe/η0大于3时,剪切速率于拉伸粘度成正比.

图2 (a;b)在不同拉伸速率下无量纲化拉伸粘度随剪切速率的变化曲线Fig.2 Curves ofdimensioniess tensile viscositg versus shear rate at different tensile rates

