基于神经网络的BFe30-1-1铜合金的本构关系模型

马艳霞，韩茂盛，刘乐乐，梁 晨

（中国船舶重工集团公司第七二五研究所，河南 洛阳 471000）

BFe30-1-1铜合金具有良好的塑形成型性能、焊接性能和超强的抗腐蚀性能，在海洋工业中得到广泛的应用，主要用于制造舰船的构件，同时BFe30-1-1铜合金也是制作冷凝管的主要材料，在电力、化工等行业也有广泛的应用，具有广阔的应用市场[1-3]。Fe30-1-1铜合金主要以管材的形式应用，而管材成形主要采用热挤压的方法，金属的热变形行为是确定挤压工艺的理论依据，因此研究材料热变形对这种高温成形工艺的制定和模具材料的选择具有重要作用[5,6]。

材料的高温变形本构关系对描述材料在热加工过程中应力与变形工艺参数之间的关系，是变形应力参数计算、实现过程数值模拟的必要基础。建立材料本构关系时，传统方法一般通过有限的实验结果进行回归，获得一些经验公式然而，材料在高温变形过程中内部的动态响应是一个十分复杂的过程，影响流变应力的因素较多且呈现高度非线性的特征。因此采用传统的方法建立的本构模型不能精确的表现出材料复杂的真实变形情况，从而降低了模型的精度。人工神经网络是由模拟人脑神经系统学习外界环境信息的过程而发展起来的一种人工智能信息处理系统，具有较高的容错性、良好的自组织、自学习、自适应和很强的联想记忆功能，是新一代信息处理工具。BP（Back Propagation）神经网络是普遍使用的一种预报模型，非常适合于解决复杂的非线性问题。利用BP神经网络对材料塑形变形过程进行建模，可在很大程度上克服传统回归方法的局限性。国内外利用人工神经网络算法进行材料本构关系模型建立的研究已经很多，但是未见到其在BFe30-1-1铜合金上的应用研究[7-9]。

本研究在Gleeble-3500热模拟机上，采用圆柱体高温压缩实验，得到BFe30-1-1铜合金在不同变形工艺参数条件下的应力值，并以此实验数据为学习样本，利用BP神经网络建立BFe30-1-1合金的本构关系模型，并对其进行误差分析，为合理制定BFe30-1-1合金热加工工艺提供指导依据。

1 实验

实验用原材料为BFe30-1-1铜合金铸锭，其化学成分见表1。将铸锭加工成ø10mm×15mm的圆柱试样并经过950℃进行均匀化处理后，在Gleeble-3500热模拟实验机上进行压缩。实验过程中，在压头与试样两端接触处夹一层石墨片进行润滑，以减少摩擦对应力状态的影响。合金的变形温度T设定为800、850、900、950℃，应变速率分 别为 0.1、1、10、20s-1，总压缩应变量为0.60。加热阶段的升温速率为10℃/s，保温3min，压缩结束后快速水冷。

表1 实验合金化学成分/Wt%

2 BFe30-1-1铜合金高温流变行为

图1为BFe30-1-1铜合金热压缩变形时的真应力应变曲线。从图中可以看出，当变形温度和应变速率一定时，流变应力随应变的增加先迅速增大，在某一临界应变处达到应力峰值，之后流变应力随着应变的增加保持平稳，具有稳态变形的特征，在低应变速率和高变形温度时，流变应力随着应变的增加呈现减小趋势。这是因为在变形过程中，变形前期加工硬化占主导地位，中间只发生了部分动态回复与动态再结晶，塑性变形比较困难。随着变形量的增大，动态回复与动态再结晶速度加快，软化作用逐渐增强。从图中还能发现，流变应力随着温度的降低而增大，随着应变速率的增大而增大，这是由于随着温度的升高，合金动态再结晶的形核率和长大速率都有所增加，进而使动态再结晶软化作用加强。同时，温度的升高带来的材料临界剪切应力下降，可能出现更多的滑移系，这些都会导致流变应力的下降。然而，随着应变速率的增大，变形时间缩短导致位错和位错攀移发展不充分，影响了回复效果，同时高应变速率使位错增值的速度增大，引起短时间内的位错堆积，使得位错运动所需驱动力也相应增大，从而导致应力增大。

3 BFe30-1-1铜合金神经网络本构模型

3.1 模型建立

BP神经网络模型是一种误差反向传播的多层前馈式网络模型，包括输入层、隐含层和输出层，输入层节点数取决于输入参数的个数，输出层节点数取决于输出参数的个数，隐含层可以包含单层或多层的神经元节点，其节点数取决于具体研究对象，而同层节点间没有任何耦合。图2为BP神经网络结构图，从图中可以看出，输入信号通过层之间的权值w调节，由输入节点传入各隐层节点，最后到达输出节点，通过误差比较修正各层的权值后再反向传播，直至达到目标误差后传出。由于连接权值w不同，输入的信号被放大、衰减或抑制，除输入层外，每一节点的输入为前一层所有节点输出值的加权和，每一点的激励输出值由节点输入、激励函数以及偏置量决定，因此该网络可以实现从输入到输出的高度非线性映射。

图1 BFe30-1-1铜合金在不同应变速率下热压缩变形的真应力-应变曲线（a）0.1 s-1 （b）1 s-1 （c）10 s-1 （d）20 s-1

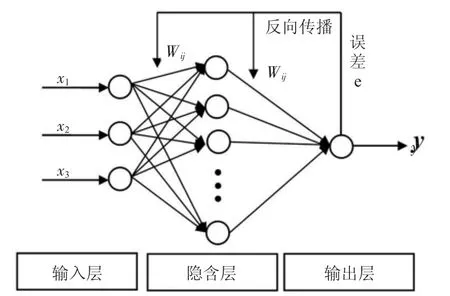
图2 BP神经网络模型

第j层的输出公式可由公式（1）表示。

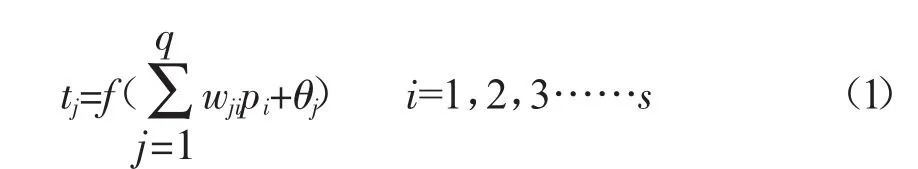
式中，tj为第j层的输出值；f为第j层地激励函数；为第i层与j层的连接权值；pi为第i层的输入值；θj为第j层的偏置量或阀值；s为第j层神经元个数；q为第i层神经元个数。

网络系统的准确性用系统的均方差来表示，如公式（2）所示。

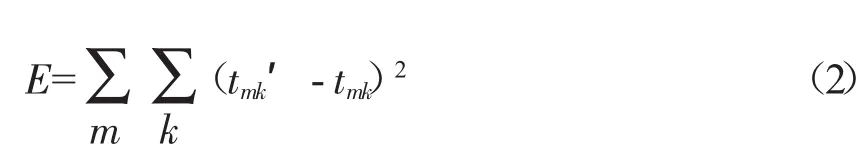
式中，E为系统均方差；m为样本个数；k为输出层神经元个数；tmk′为期望输出值；tmk为实际输出值。

在网络学习过程中，若系统均方差未满足要求则调整权值，然后反向传回网络系统重新计算，直至网络误差满足要求或达到指定的学习次数。本文采用三层BP神经网络模型，输入层包含变形温度T、真应变ε和应变速率ε˙三个节点，输出层为真应力σ。

3.2 数据预处理

从图1的真应力-应变曲线中选取288个数据分为两组，其中192个作为训练样本，96个用于验证。由于变形温度、变形速率和真应变的数值单位不同，数值相差较大，这样会促使量级大的数值在网络训练中起主要作用，影响网络的判断，因此在建立网络之前必须对所有数据进行相关处理，从而去除各数值之间的量纲差异，使所有的数据处于同等重要的位置，此外还可以保证网络的稳定[10]。

根据BP神经网络对输入输出范围的要求，按公式（3）对训练样本的输入、输出参数进行归一化处理。

式中，X实验所获得的原始数据，Xmin和Xmax为原始相应数据的最小值和最大值，X′为参数X归一化处理后的数值。

3.3 模型训练

采用Matlab将归一化后的训练样本对BP神经网络进行训练，转移函数为“tan sigmoid”和“pure linear”，训练函数为“Trainlm”，训练目标误差为 10-3。隐含层神经元数目的选择是一个非常复杂的问题，数目太少会导致训练出来的网络容错性差，不能识别参与未参与训练的样本；数目过多会导致学习时间过长，误差不一定最佳，因此隐含层单元数存在一个最佳值，通常来说，隐含层神经元数目通过经验公式（3）来确定范围：

式中，n1为隐含层单元数，m为输出层神经元数，n为输入层单元数，a为0～10之间的常数。

为了确定隐藏层的神经元的数量，从两个神经元开始，采用试错法进行一一训练，最终发现当隐含层神经元个数为12时，网络性能最好。BP网络模型经过880个循环达到稳定状态。

3.4 结果分析

如图3所示，将神经网络预测得到的流变应力值进行反归一化处理，并与验证样本进行对比。从图中可以看出，BP神经网络预测的流变应力与实验数据的相关性较好，拟合相关系数达到0.9999。

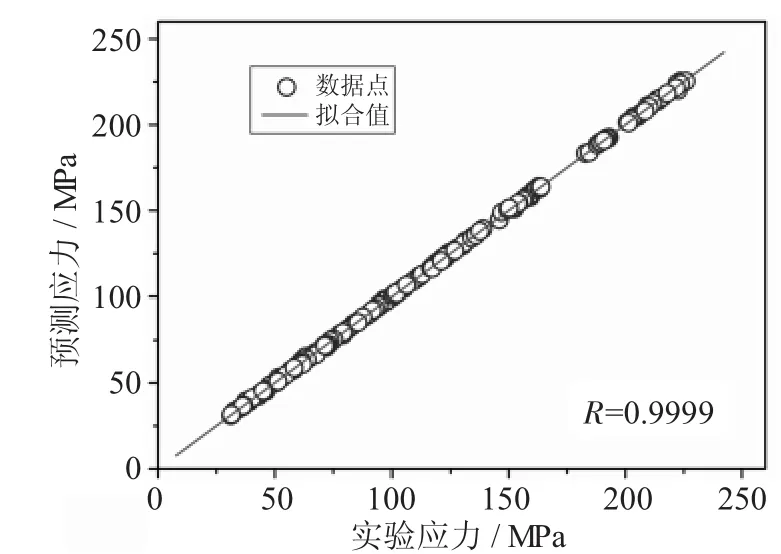
图3 BP神经网络模型预测流变应力值与实验值的关联性曲线

表2为应变速率为0.1s-1时不同应变、变形温度下的部分流变应力值与神经网络模型预测值之间的误差情况，从表中能够发现，预测值与实际值非常接近，相对误差在5%以下。

如图4所示为采用BP神经网络模型预测的BFe30-1-1铜合金流变应力与实验值的对比图。从该图中可以看出，采用BP神经网络模型预测的流变应力值与实验值吻合良好，而且具有较高的精度。

为全面考察所建立的本构模型的精度，根据公式（4）计算可得到拟合度δ：

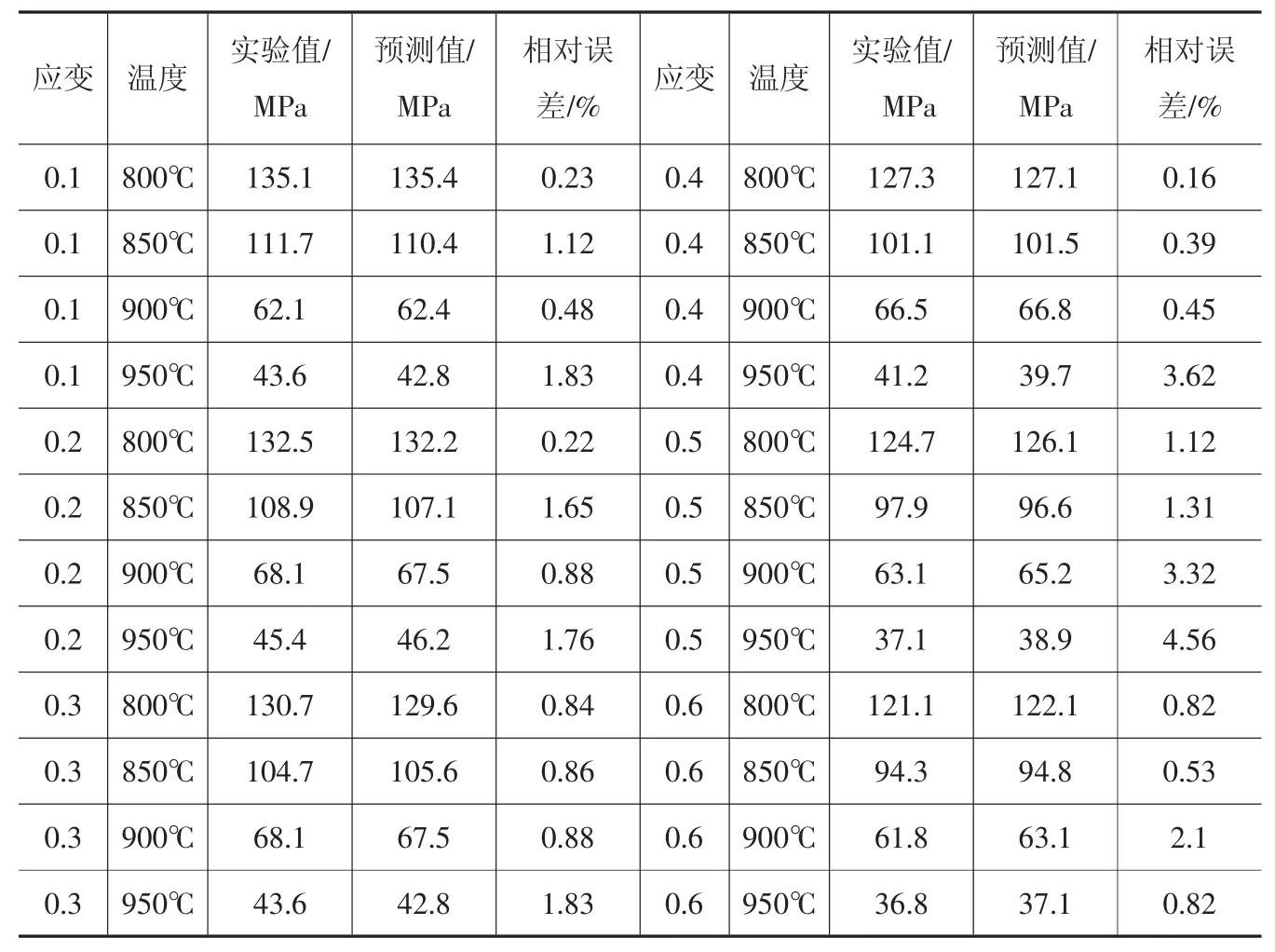
表2 应变速率为0.1s-1时神经网络模型预测值与实验值对比

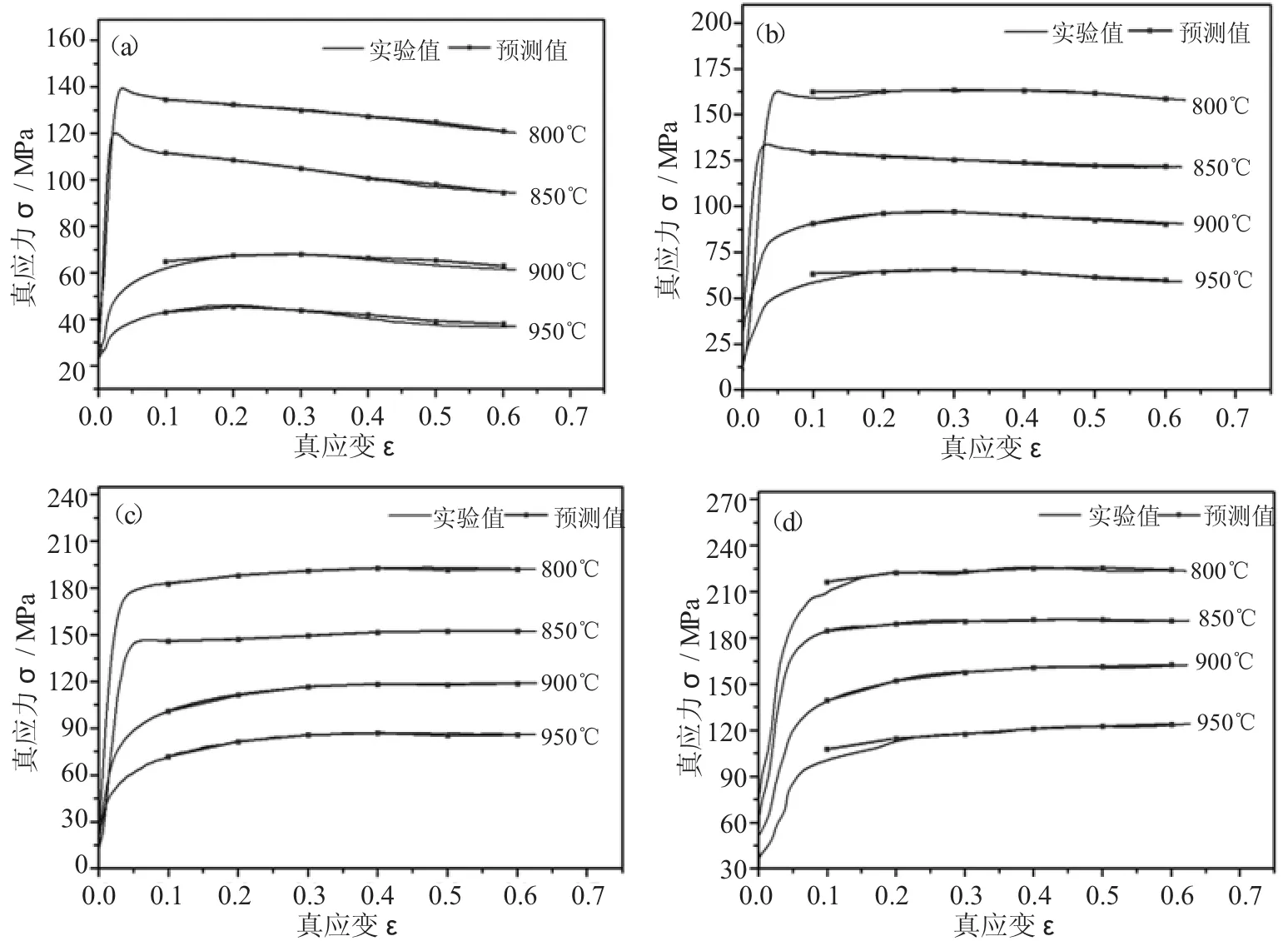
图4 采用BP神经网络模型预测的BFe30-1-1铜合金流变应力值与实验值的对比（a）0.1s-1 （b）1s-1 （c）10s-1 （d）20s-1

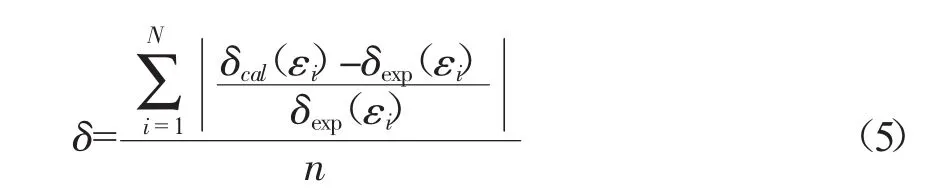
式中，δexp（εi）为流变应力的实验值，δcal（εi）为通过BP模型计算的预测数据，n为实验分析数据点的个数。经计算，得到的平均相对误差为1.65%，进一步证明BP神经网络模型具有较高的精度，可满足工程计算要求。

4 结论

（1）通过热压缩实验得到了BFe30-1-1铜合金在应变速率为0.1～20s-1和变形温度为800～900℃的真应力-应变曲线，发现B30铜合金的流变应力随着变形温度的增加而降低，随着应变速率的增大而增大。

（2）利用BP神经网络算法，建立了BFe30-1-1铜合金高温压缩变形过程的本构关系模型，结果显示计算值和预测值的拟合相关系数达到0.9999，得到的平均相对误差为1.65%，表明BP神经网络模型具有较高的精度，能较好的满足工程计算的要求。