圆柱锻件冲孔极限尺寸的参数化预测

叶 明，高锦张，马武江，王兴中

（1.东南大学 材料科学与工程学院，江苏 南京 211189；2.上海新闵重型锻造股份有限公司，江苏 东台 224200）

在现代工业生产中，大型空心锻件的使用越来越多，例如在核电行业中，大型空心锻件应用于主管道锻件、反应堆压力容器和蒸汽发生器等，都属于核岛内七大关键设备[1-3]。

为了制订空心锻件冲孔工艺参数，对圆柱锻件冲孔极限尺寸进行模拟研究。在圆柱锻件进行冲孔过程中，较细的冲头直径常常会发生弯曲现象，造成锻件报废甚至安全事故。这是因为在冲孔时，冲头的轴向压力超过了冲头类长杆件的临界压力，发生压杆失稳现象[4]。

因此，本文以圆柱锻件冲孔过程为模拟研究对象，主要研究在圆柱锻件的高径比在1.0～3.0之间，最小合理冲孔尺寸的变化规律，目的在于寻找任意圆柱锻件冲孔过程的合理最小冲孔尺寸的范围，为实际生产提供理论依据，提高安全系数。

1 有限元模型的建立及模拟方案

1.1 有限元模型的建立

本文选用DEFORM-3D有限元模拟软件分析圆柱锻件冲孔的锻造过程，对冲孔工艺进行模拟分析，坯料模型尺寸与实际尺寸以1:1进行建模。其中冲头选用平底冲头，在冲头端部设有圆角r为20mm，如图1所示。

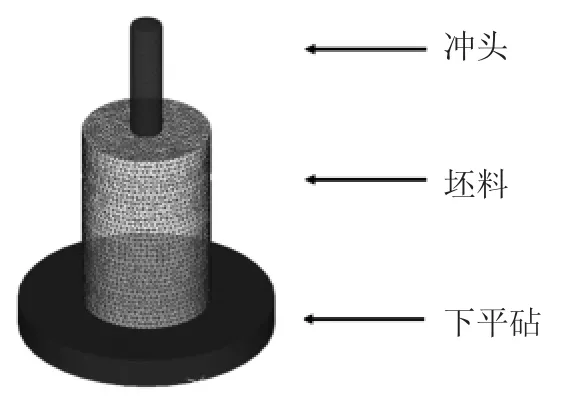
图1 数值模拟模型

坯料的材料模型是P91耐热合金钢，设为塑性体，冲头及下平砧采用H13钢，不发生塑性变形，均设置为刚体。由于坯料冲孔过程中心部为主要变形区域，在网格划分过程中，采用绝对网格划分，并对主要的变形区域进行网格细分。有限元模型参数设置如表1所示。

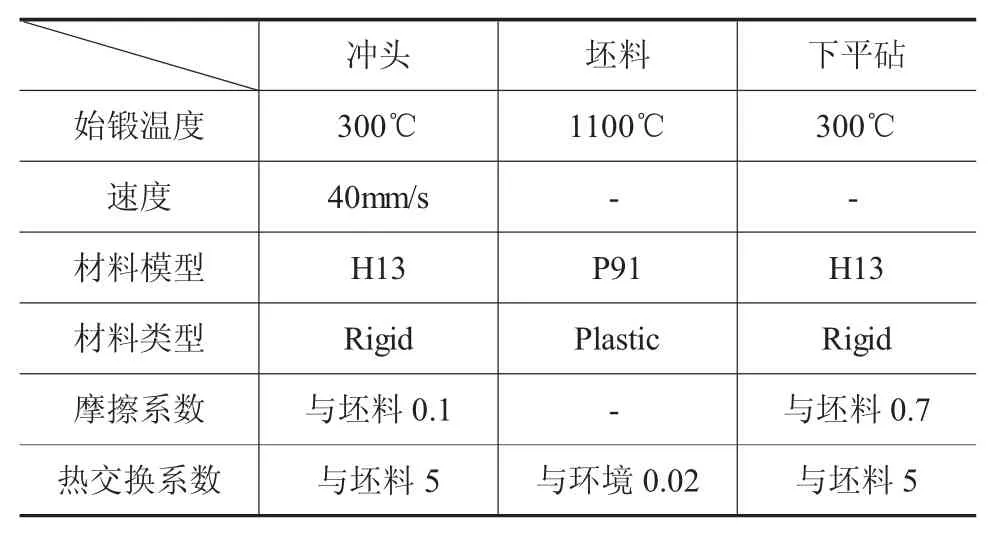
表1 前处理工艺参数的选定

1.2 模拟实验方案

选取高径比（H/D）为 1.0、1.5、2.0、2.5 和 3.0 的圆柱锻件，其中H为圆柱锻件的高度，D为圆柱锻件的直径。在每个高径比下，选择几种坯料尺寸，如表2所示。第一阶段为正冲，冲孔深度为坯料高度的一半。同时为方便夹持冲头，冲头长度取H/2+200mm。由于圆柱形坯料上下对称，现只分析坯料一半时的成形过程。

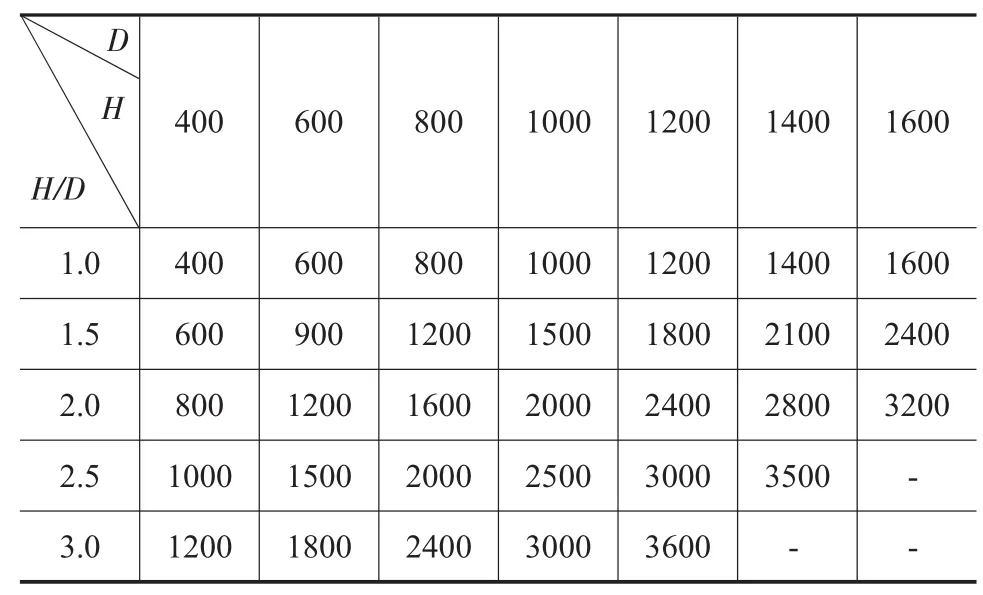
表2 不同H/D下，不同坯料直径的最大冲孔尺寸/mm

2 圆柱锻件冲孔尺寸下限的确定

2.1 孔径比下限的理论基础

根据选取的圆柱形坯料尺寸，在模拟冲孔过程中保证冲头不发生失稳的情况下，探究坯料内孔直径的最小值，定义最小的孔径比dmin/D。

压杆稳定计算中，需要采取不同的安全系数。在实际生产中，压杆的稳定按如下条件计算：

式中：Fcr——临界载荷；

Fa——工作载荷；

n——压杆的规定稳定安全系数。

根据文献[5]，取 n=2。

其中，圆柱形冲头的临界载荷Fcr满足的条件为：

式中：E——冲头弹性模量；

d——冲头直径；

μ——长度系数；

L——冲头长度。

冲头采用H13钢，其弹性模量E=210GPa，压杆长度系数μ=2。

2.2 圆柱锻件冲孔尺寸下限的研究

选择H/D=1.5、直径D为ø1000mm、高度H为1500mm的坯料进行模拟分析。冲头直径分别取150mm、200mm、250mm、300mm、350mm、400mm， 对应的孔径比分别为 0.15、0.20、0.25、0.30、0.35、0.40，冲头长度均为950mm。得到冲孔的载荷行程曲线如图2所示。

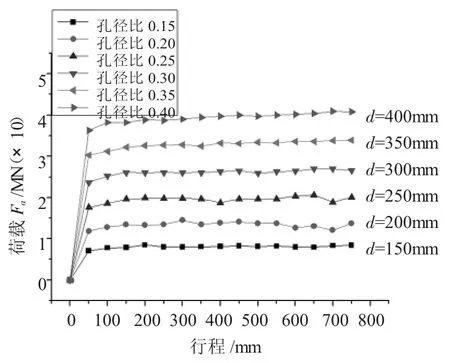
图2 冲孔时冲头载荷行程曲线

由图2可见，对于几种尺寸的冲头在冲孔初始阶段，冲头的成形载荷均出现急剧增大，随着冲头行程增加，成形载荷均各自趋于稳定值；图3是在半冲结束的情况下，各种直径冲头冲孔的最终成形载荷与冲头直径的对应关系曲线图。由图3可知最终成形载荷随着冲头直径尺寸增大而增大。

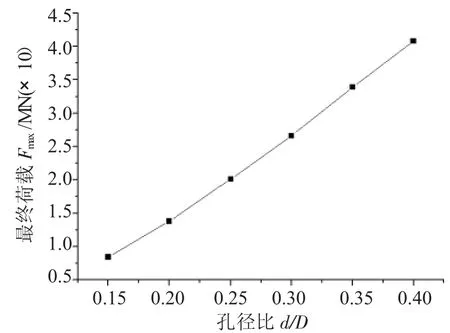
图3 最终载荷与冲头直径关系图

研究发现最终载荷与冲头直径的规律在表2中H/D 为 1.0、1.5、2.0、2.5、3.0 各种情况下依然成立，即高径比一定及毛坯直径一定时最终成形载荷均随着孔径比的增大而增大。

为了确定冲孔毛坯尺寸为ø1000mm×1500mm下的冲孔孔径比下限，改变冲头直径大小，对坯料进行冲孔模拟实验，提取冲孔过程中的最终成形载荷Fmax。同时根据公式（2）计算的各个尺寸下冲头的临界载荷Fcr进行稳定条件处理，得到曲线分析图4所示。

由图4可知，在各个冲孔直径尺寸下冲头的临界载荷曲线与2倍的冲头的稳定载荷曲线相交一点P，其落在横坐标d处。当冲头直径小于d时，Fcr/Fmax≤2，冲头的临界载荷值小于2倍的冲头的稳定载荷，不满足公式（1），在冲孔过程中会发生失稳现象，造成事故；当冲头直径大于d时，即满足式（1）要求，即冲头冲孔时不会发生失稳，可以保证生产安全。因此，对应的横坐标d为稳定冲孔过程的最小冲孔直径dmin。

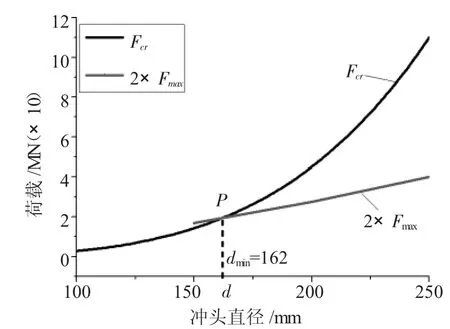
图4 冲孔过程稳定载荷与临界载荷曲线

3 不同H/D下，圆柱锻件冲孔的尺寸下限

依次选取表2中坯料尺寸数据，分别对高径比H/D为 1.0、1.5、2.0、2.5、3.0 的圆柱锻件进行冲孔模拟实验，计算相应的坯料冲孔尺寸的下限值，如表3～表7。同时为了更直观地了解最小冲头直径dmin与坯料直径D之间的关系，将其绘制成曲线，并进行一次线性拟合，如图5～图9所示。

由图5、图6、图7、图8、图9可知，在高径比在1.0、1.5、2.0、2.5 和 3.0 时，模拟结果和相对应的拟合曲线重合度较高。因此，在一定高径比下圆柱锻件冲孔最小冲头直径与坯料直径参数化关系的建立具有理论基础。

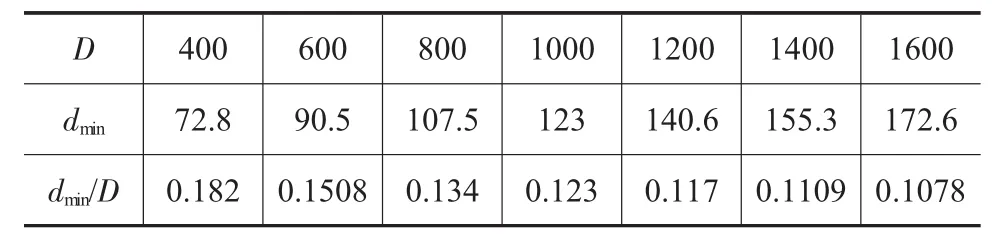
表3 H/D=1.0/mm

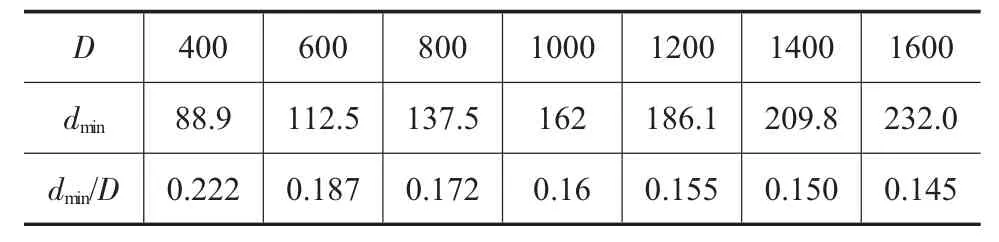
表4 H/D=1.5/mm

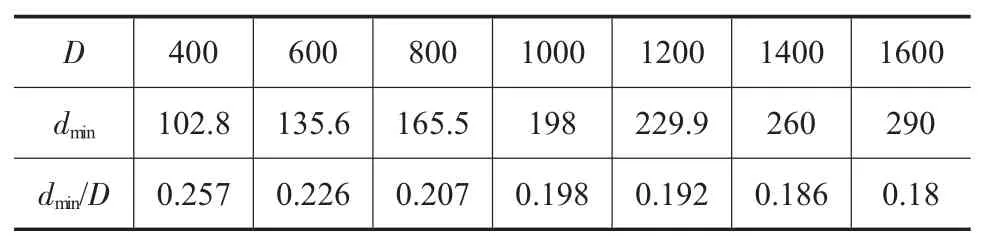
表5 H/D=2.0/mm

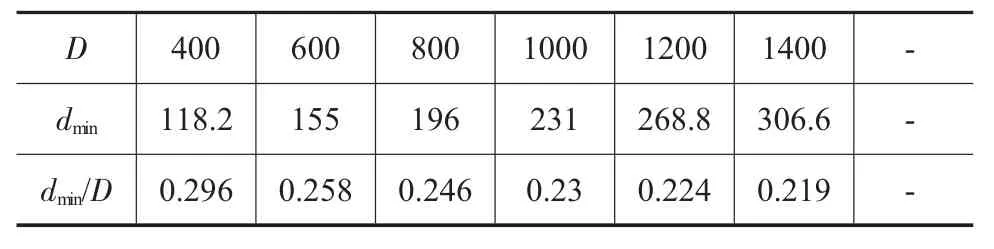
表6 H/D=2.5/mm

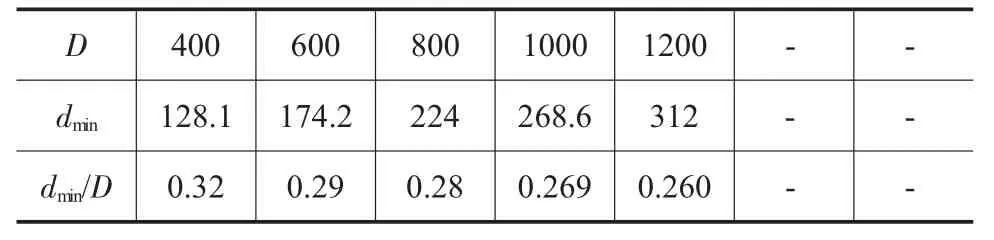
表7 H/D=3.0/mm

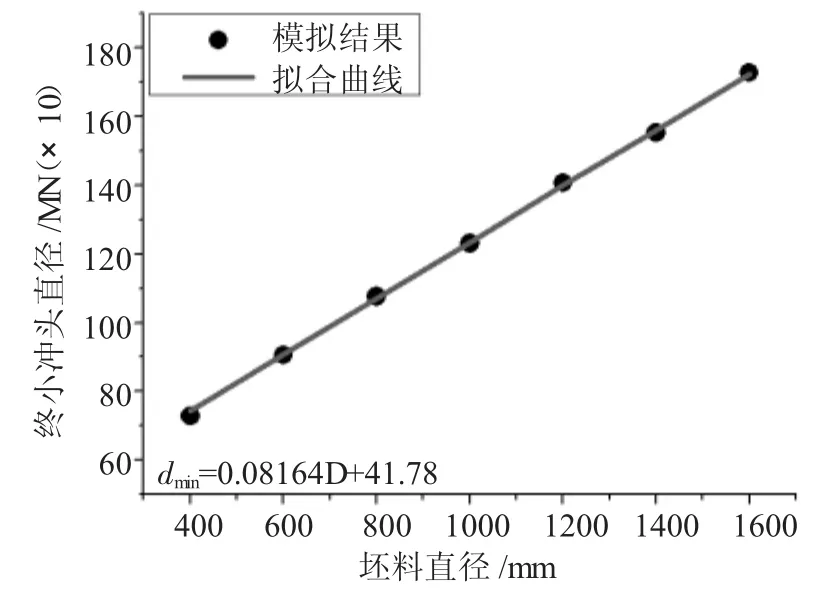
图5 H/D=1.0最小冲头直径随坯料直径的变化关系

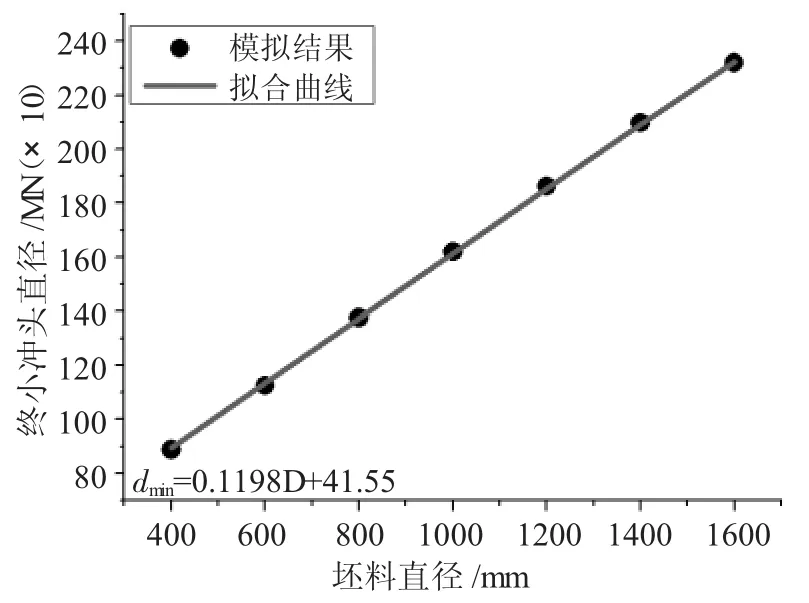
图6 H/D=1.5最小冲头直径随坯料直径的变化关系

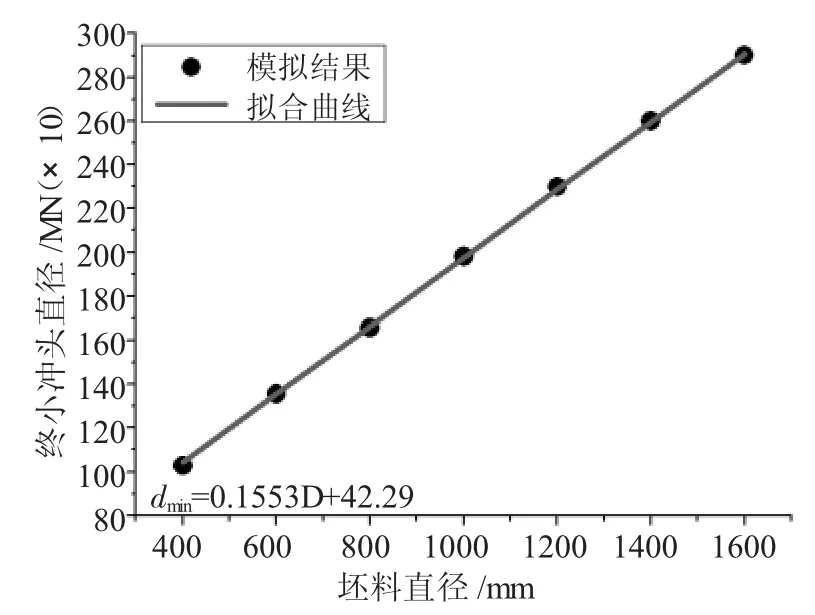
图7 H/D=2.0最小冲头直径随坯料直径的变化关系

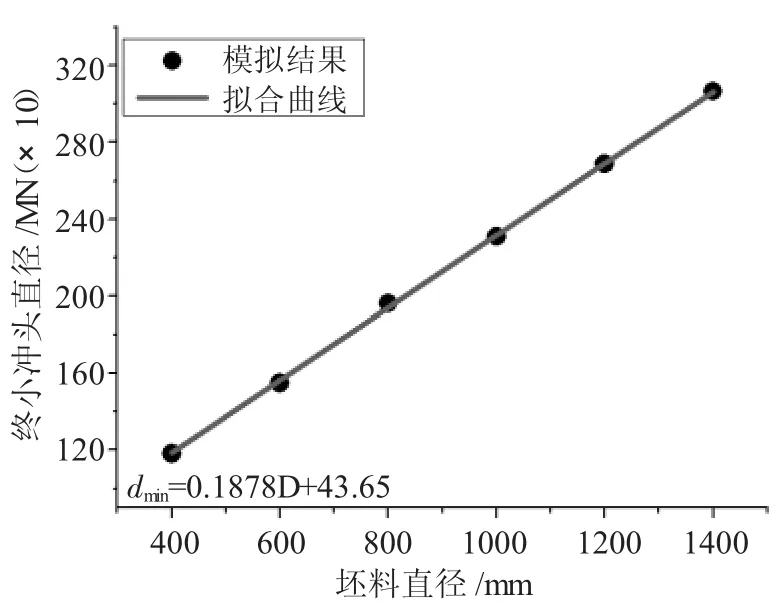
图8 H/D=2.5最小冲头直径随坯料直径的变化关系

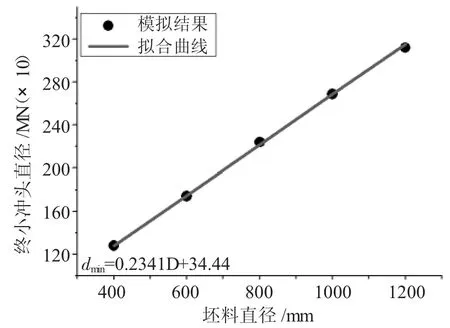
图9 H/D=3.0最小冲头直径随坯料直径的变化关系

4 一定高径比时圆柱锻件冲孔最小冲头直径与坯料直径参数化关系的建立

4.1 参数化的建立

根据图5～图9所示，在高径比H/D在1.0～3.0之间，不同直径坯料下的最小冲头直径随着坯料直径的增大而增大，并且呈线性增大关系。为了观察最小冲头直径随坯料直径的变化关系在不同高径比下的变化趋势，将图5～图9汇总成图10。

将不同高径比下拟合曲线作参数化方程，如公式（3）～公式（7）所示。

在不同高径比下，坯料的最小冲头直径与坯料直径的变化关系不同。因此，在实际锻件冲孔过程中，若坯料高径比为 1.0、1.5、2.0、2.5、3.0 时，可以利用拟合公式（3）～公式（7），根据坯料直径来计算最小冲头直径。

图10 不同高径比下最小冲头直径随坯料直径变化关系

同时针对高径比在 1.0～1.5、1.5～2.0、2.0～2.5、2.5～3.0时，最小冲孔直径与坯料直径的关系可以在图10中进行插值查表得出。

4.2 参数化验证

为了验证在高径比为 1.0、1.5、2.0、2.5、3.0 时，圆柱锻件直径在400mm～1600mm的任意尺寸下，最小冲头直径与坯料直径关系满足参数方程（3）～（9）。选择直径为 500mm、700mm、900mm、1100mm、1300mm和1500mm的圆柱锻件，高径比分别为1.0、1.5、2.0、2.5、3.0尺寸的坯料进行冲孔模拟实验，尺寸数据如表8。按照上文冲孔方案进行冲孔模拟实验。

将冲孔模拟获得圆柱锻件冲孔尺寸和参数方程得到的尺寸对比，得到表9～表13。其中：

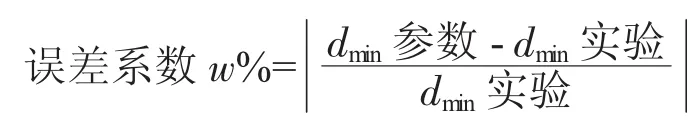
由表9～表13可知，针对参数化表达式的验证，表8中各尺寸圆柱锻件冲孔模拟实验中获得的极限尺寸与参数化表达式获得的相应尺寸下的尺寸数据之间误差系数w%＜3.0%。证明圆柱锻件冲孔尺寸下限的参数化具有一定的可信性。

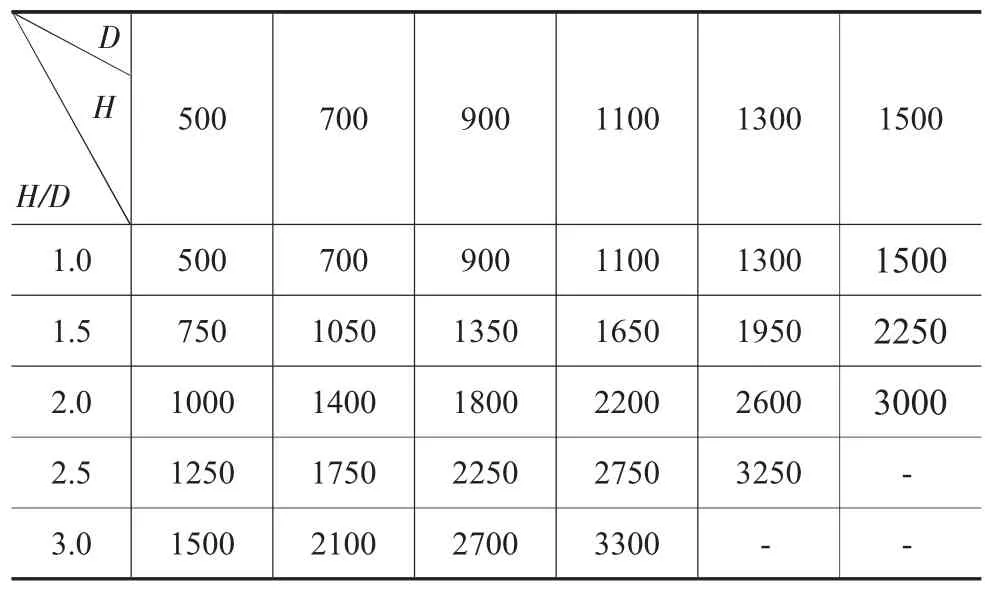
表8 圆柱锻件尺寸/mm

5 结论

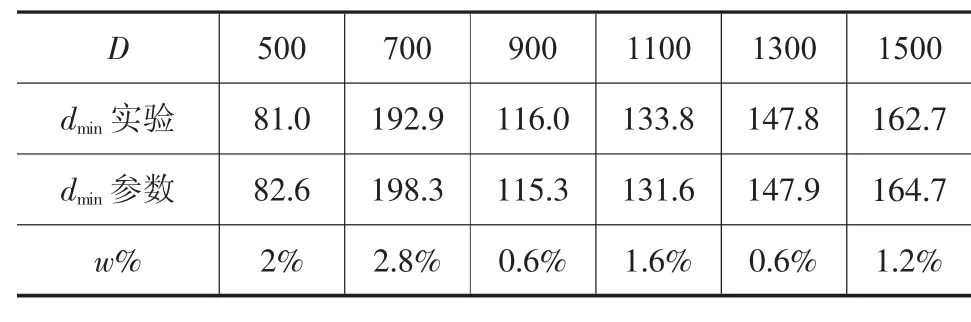
表9 H/D=1.0尺寸对比/mm

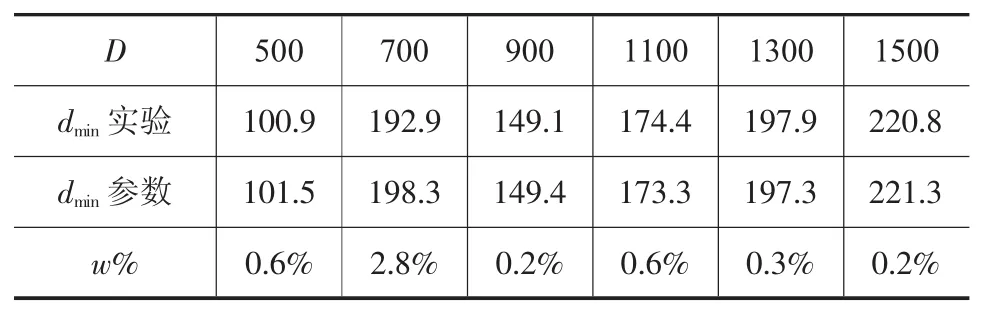
表10 H/D=1.5尺寸对比/mm

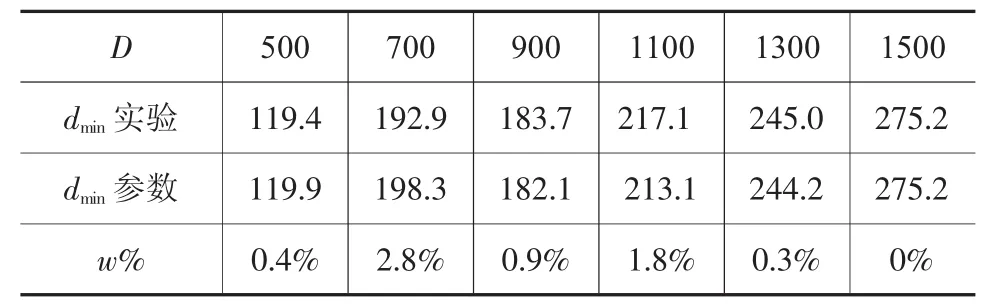
表11 H/D=2.0尺寸对比/mm

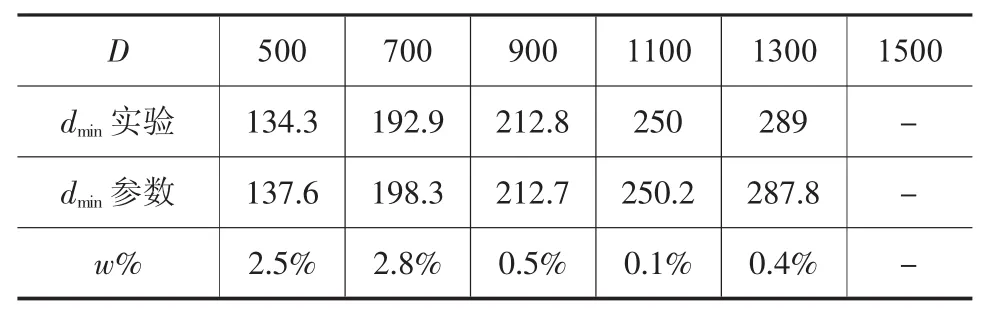
表12 H/D=2.5尺寸对比/mm

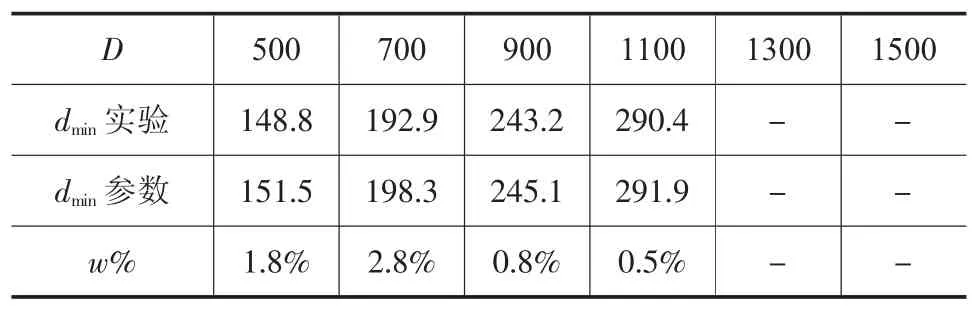
表13 H/D=3.0尺寸对比/mm

本文选取高径比为 1.0、1.5、2.0、2.5、3.0 的圆柱锻件，在不同圆柱锻件直径尺寸下进行冲孔工艺的模拟分析，得到以下结论：

在高径比 H/D 为 1.0、1.5、2.0、2.5 和 3.0 时，不同直径坯料下的最小冲孔直径随着坯料直径的增大而增大，并且呈线性增大关系；

若坯料高径比在1.0、1.5、2.0、2.5和 3.0时，可以利用参数化公式，通过坯料直径来计算最小冲孔直径；

当坯料高径比 1.0～1.5、1.5～2.0、2.0～2.5、2.5～3.0时，最小冲孔直径与坯料直径的关系可以通过插值查表得出。