一类奇异非线性微分系统正周期解的存在性

陈瑞鹏，李小亚

(北方民族大学 数学与信息科学学院， 宁夏 银川 750021)

1 研究背景

近年来，诸多学者致力于研究一阶非线性微分方程

x′+a(t)x=f(t，x)

(1)

周期解的存在性及其相关性质[1-13]，其中a∈L1(R/ωZ，R+)，非线性项f∈Car(R/ωZ×[0，∞)，R)，即f|[0，∞]∶[0,ω]×[0，∞)→R是一个L1-Carathéodory函数。作为一类重要的数学模型，该方程旨在描述与呼吸、心律失常及血细胞生成等密切相关的多种人体生理过程[1-3]。

同时，方程(1)所对应的一阶微分系统备受关注[14-16]。2011年，Wang[15]研究了带有奇异非线性项的微分系统：

λbi(t)fi(x1，x2，…,xn)，

i=1，2，…，n

(2)

其中ai，bi∈C(R，[0，∞))为ω-周期函数且满足

fi为连续的严格正函数且在(0，0，…，0)处有奇性。 运用Krasnoselskii不动点定理，该文证明了当参数λ>0充分小时，系统(2)存在2个正周期解.然而并未得到参数较大时正周期解的存在性结果。随后，Chen等[16]对Wang的结果做了进一步推广和改进，并证明了存在λ0>0，使得当0<λ<λ0时，系统(2)至少存在2个正周期解；当λ=λ0时，系统(2)至少存在1个正周期解；当λ>λ0时，系统(2)不存在正周期解。

方便起见，记ξ*和ξ*分别为ξ∈L1(0，ω)的本性上界和本性下界，若ξ≥0，a.e.t∈[0，ω]且在某个正测集上严格为正，则记为ξ>0，受上述文献启发，本文将为一阶非线性微分系统

(3)

建立正周期解的存在性结果。虽假设非线性项g1和g2在0处仍具有奇性，但是将给予这种奇性更为精确的刻画，即假设：

(A1)a，h∈L1(R，[0，+∞))为ω-周期函数且满足

(A2)c1，c2∈L1(R，[0，+∞))为ω-周期函数，gi|[0,ω]:[0,ω]×(0,∞)→R为L1-Carathéodory函数，i=1，2;

s∈[1，∞)，a.e.t∈[0，ω]，i=1，2

s∈(0，1)，a.e.t∈[0，ω]，i=1，2

注1 条件(A1)保证了线性方程u′+a(t)u=0(v′+h(t)v=0)是非共振的，其相应的Green函数为

引理1[17-18](Schauder不动点定理) 设K是Banach空间S中的一个非空有界闭凸集，且算子A∶K→K全连续，则A在K中必存在不动点。

2 主要结果及证明

本节将在更为精确的奇异性假设(A3)下，运用Schauder不动点定理为一阶奇异微分系统(3)建立正周期解的存在性结果。

首先，定义

(4)

δi=maxνi，βi，ηi=maxαi，μi，

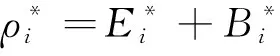
(5)

定理1 假设(A1)(A2)和(A3)成立，若γ1*≥0，γ2*≥0，则系统(3)存在一个正ω-周期解。

证明记Sω为连续的ω-周期函数全体构成的空间。定义算子A(u，v)=(A1u，A2v):Sω×Sω→Sω×Sω为

不难验证A是一个全连续算子，并且系统(3)的一个ω-周期解恰为A的一个不动点。 令

K={(u，v)∈Sω×Sω∶r1≤u(t)≤R1，

r2≤v(t)≤R2，∀t∈[0，ω]，Ri>1，i=1，2}

其中R1>r1>0，R2>r2>0是待定常数。由引理1可知若全连续算子A把有界闭凸集K映入自身，则A在K中存在不动点，从而系统(3)必存在正ω-周期解。

对给定的函数φ，记

Ji1={t∈[0，ω]ri≤φ(t)<1}

Ji2={t∈[0，ω]1≤φ(t)≤Ri}，i=1，2

任取(u，v)∈K，由Gi(t，s)和gi的正性及条件(A3)可得

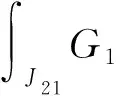
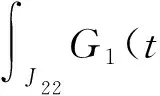
同理，对任取的(u，v)∈K，有

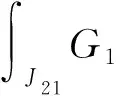
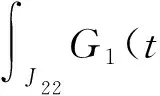
通过类似讨论可得

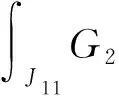
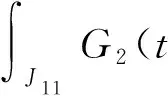
以及

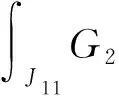
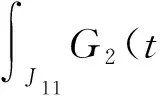
现在，只需确定常数Ri，ri，它们应满足Ri>ri>0，Ri>1，且使得下列各式同时成立：

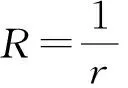
此时，可选取R>1充分大，则由条件ηi<1和νi<1可知以上各式同时成立，于是系统(3)必存在一个正ω-周期解。

推论1 假设(A1)(A2)和(A3)成立，则系统

(6)

存在一个正ω-周期解。

证明由ci(t)≡0结合式(4)易得γi(t)≡0，故γ1*=γ2*=0。再由定理1知结论成立。

定理2 假设(A1)、(A2)和(A3)成立且

(7)

(8)

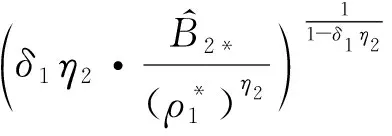
(9)

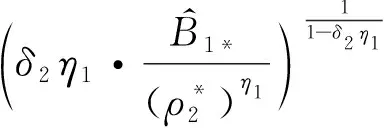
(10)

则系统(3)存在正ω-周期解。

证明定义有界闭凸集

K={(u，v)∈Sω×Sω∶r1≤u(t)≤R1，

r2≤v(t)≤R2，t∈[0，ω]，Ri>1>ri>0}

其中Ri，ri仍为待定常数。由引理1知若A把有界闭凸集K映入自身，则A在K中存在不动点，从而系统(3)存在一个正ω-周期解。

任取(u，v)∈K，由条件(A1)、(A3)和R2>1>r2可得

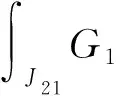
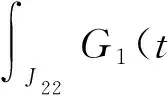
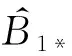
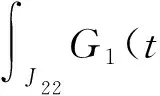
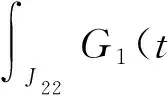
通过类似估计可得

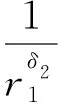
现在，只需确定常数Ri，ri，它们应满足Ri>1>ri>0，i=1，2，且使得下列各式同时成立：

(11)

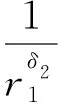
(12)

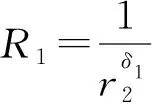
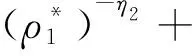
(13)

时，式(12)中第1个不等式成立。定义函数

·r2δ1η2

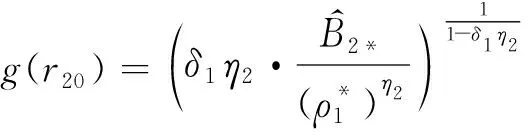
时式(12)中第1个不等式必成立，而上式恰为条件式(9)。

这恰为已知条件式(10)。最后，由条件式(7)和(8)易知Ri>1>ri>0成立，从而系统(3)必存在正ω-周期解。