S-Harris:一种改进的角点检测算法

孙万春，张建勋，朱佳宝，陈虹伶，郑集元

(重庆理工大学 计算机科学与工程学院, 重庆 400054)

角点检测[1]是一种计算图像中角点的数学方法，目前主要运用在图像匹配、监控视频采集、目标跟踪、图像拼接、3D模型的建立等计算机视觉领域，通过提取图像中的一些特殊兴趣点，将其定义为角点，其是局部特征提取时间复杂度的关键性因素。在图像中，角点检测到的兴趣点对局部特性的描述也起决定性作用[2]，同时由于角点的特殊性，其并不受旋转、尺度变化等干扰，因此对其进行深入探究具有非常重要的意义。

目前，角点检测方法分为三大类[3]：① 基于灰度图像的角点检测。计算边缘曲率来判断角点的存在，其主要和边缘强度、边缘方向的变化率有关。目前此类方法主要包含Harris算法、SUSAN算法、Moravec算法等。② 基于二值图像角点检测。由于经过二值化处理，计算复杂性较低。袁宁等[4]利用细化图像的特殊性，采用形态骨架来提取角点。由于二值图像的角点检测方法的一些计算过程在灰度图像和轮廓曲线方法中均有采用，所以目前单独对此方法进行研究的人较少。③ 基于轮廓曲线的角点检测。通过高低尺度对目标图像分离出轮廓曲率较大的值，再通过阈值参数的选定筛选出角点，常用的算法包括Mokhtarian的CSS算法[5]。

由于Harris算法计算较为简单，并且计算结果比较稳定[6]，国内外众多学者均采用该算法进行相关的工作。许佳佳等[7]通过构建高斯尺度空间优化Harris算法的尺度特性，但是该算法并未针对Harris算法本身进行相关算法上的优化，不利于后期深入拓展。葛盼盼等[8]提出了一种Harris和Surf融合特征方法，利用Surf对尺度变化的鲁棒性和Harris算法的特征提取稳定性来进行图像匹配。张从鹏等[9]利用Harris角点检测效果的稳定性，将其运用到了矩形窗口检测上。王民等[10]针对Harris算法在抗噪性和实时性能上的劣势，提出了一种基于像素点灰度差的角点检测算法，该算法虽然提高了检测的效率，但是对于一些灰度变化较小以及纹理信息丰富的图像，会因为灰度差丢失特征信息。

针对上述算法存在的问题，提出了一种灰度差分均值的思想。此外，针对算法在窗口滑动过程中对重叠像素点进行重复计算的情况，引入了积分图像的思想，。

1 Harris角点检测及其缺陷

1.1 Harris角点检测方法

Harris角点检测算法是由C.Harris和M.J.Stephens在1988年提出的一种基于信号点特征的提取算法[11-12]，其理论基础是Moravec算法。Moravec算法对图像中的中心像素点定义一个局部矩形检测窗口，该窗口可以任意在水平、垂直、正反对角线等各个方向上进行微移，在不断的微移过程提取矩形窗口的平均能量变化，并通过泰勒级数的思想来计算窗口的变化值，计算出角点。对于给定的一个图像像素中心点C(x,y)，其任意微移后的灰度强度变化可表示为

[I(u,v)-I(u+Δx,v+Δy)]2

(1)

式(1)中矩形窗口的移动方向及其移动方向的相关权重u、v定义如下：

(2)

由式(2)定义区间可知，通过式(1)的窗口滑动，总共会产生8种不同方向的强度变化，如图1所示。

图1 窗口滑动任意方向示意图

从图1可知：Harris算法解决了Moravec算法在任意方向移动的难点。对式(1)的子项进行泰勒展开，并取其近似值，结果如式(4)所示。

I(u+Δx,v+Δy)=I(u,v)+Ix(u,v)·

Δx+Iy(u,v)·Δy+…+Rn(u,v)≈

I(u,v)+Ix(u,v)·Δx+Iy(u,v)·Δy

(4)

将求得的近似值式(4)代入自相关函数中可得：

(5)

通过式(5)可以看出：该算法解决了Moravec算法在任意方向移动的难点，其中Ix和Iy分别表示图像在水平方向和垂直方向的导数。对式(5)中子项[Ix(u,v)·Δx+Iy(u,v)·Δy]2进行展开，结果如下：

2Ix(u,v)Iy(u,v)ΔxΔy=

(6)

将式 (6)代入原自相关表达式 (1)中可得：

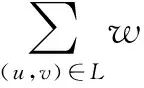
[Ix(u,v)·Δx+Iy(u,v)·Δy]2=

(7)

式(7)中M表示为

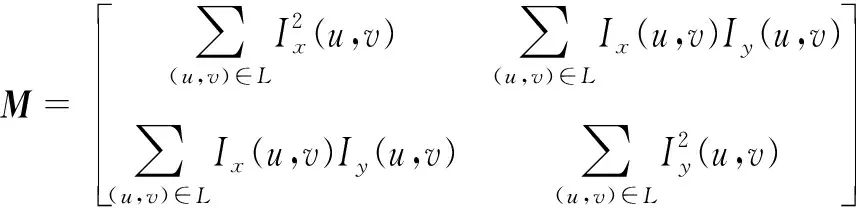
(8)

由式(8)可知其为矩阵，假定其特征值分别为λ1、λ2，数学意义如图2所示。

分析可知：特征值的大小有以下的性质：① 在光滑区域λ1、λ2相近且差值较小；② 在边缘、线段λ1、λ2差值较大；③ 在角点区域λ1、λ2相近且差值较大。

Harris算法针对计算特征值来判别角点的方法计算量大的问题，定义了一个角点响应值R判断准则：

R=detM-α·(traceM)2

(9)

式(9)中：detM是矩阵M的行列式；traceM是矩阵M的迹；α是经验常数值，通常取值范围为0.04～0.06。因此，通过式(9)即可求得一幅图像中所有的角点。

1.2 Harris算法存在的不足

在算法的实际运用中发现以下问题：① 在矩阵窗口的滑动过程中容易受到噪声的干扰，对角点的最终位置等产生较大的影响。② 在角点响应[13]的计算的过程中，容易产生相邻像素的重叠，增加计算的复杂度。③ 阈值的选择对角点的判断有直接关系。在Harris算法中，阈值的选取只能通过经验来进行判断。阈值过大不仅会丢失角点信息，还会造成伪角点的产生；阈值较小不仅降低了角点的质量，也会增大对噪声的敏感。

图2 λ1、λ2特征值相关数学意义

2 S-Harris:改进的角点检测算法

2.1 算法改进思想

针对Harris算法存在的上述问题，特别是其不具备抗噪的特性，提出了一种灰度差分均值的思想。该方法首先对图像中滑动窗口中的像素点，计算其邻域周边像素点的像素均值，对求得的均值再计算其灰度差值，通过求得的灰度差值来计算其灰度差均值，从而计算其方差。针对其在窗口滑动过程中对重叠像素点重复计算的情况，引入了积分图像的思想。

2.2 自适应灰度差分

,i=0,1,…,P-1

(10)

(11)

根据对比度值及其均值，计算标准差D：

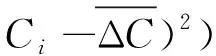
(12)

由标准差近似估计离散度σ:

(13)

对像素中心点C(x,y)进行二值化编码：

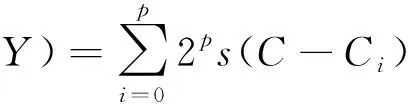
(14)

其中s(t) 是量化函数，定义如下：

(15)

从上述离散度的计算过程看，离散度会随着每个邻域的变化而变化，这说明离散度对选取点具有自适应性。同时离散度受像素点选取的变化影响较小，因此其在同一类情况下的离散度变化也不大，说明离散度都能有效地描述选择的像素点及其变化关系。因此，把离散度σ选作自适应阈值具有有效性。

2.3 积分图像

积分图像[15]在对图像中矩形区域特征进行描述时具有运算速度快的特性。在图像矩形特征计算过程中，一旦计算出积分图像，则可以在常量的时间内计算出该积分图像内部任意大小矩形区域的特征信息，可以在降低运算量的同时提升计算机处理速度。

由图3可知，对于任意一个滑动窗口区域∑S，可得到：

∑S=iiA+iiC-iiB-iiD

(16)

其中ii(x,y)定义如下：

(17)

依据上述公式改进式(1)，便可解决窗口滑动过程中重复计算问题。

图3 积分图像

3 实验结果及分析

3.1 实验环境

为了验证改进的Harris算法在抗噪、检测时间上可取得良好效果进行实验。实验平台环境为DELL Windows 10系统，基于VS2012开发环境，采用Opencv2.4.13图像处理库。Intel i5-3470,3.20 GHz,8 GB 内存空间。

3.2 实验结果

为了验证本文所提出的灰度差分理念以及引入积分图像思想后对Harris算法的改进有效性，与Harris算法角点检测结果进行了比较。

3.2.1 光噪下的角点检测准确性

在验证Harris算法抗噪性能时，选择了一张重庆理工大学校门的图片。对于实验图，分别对其高斯噪声做均值为0.02、0.05和0.1处理，处理效果如图4所示。

图5为使用Harris算法后，原始图像和高斯噪声处理后的实验效果。

图6为使用S-Harris算法后，原始图像和高斯噪声处理后的实验效果。

图4 噪声前后对比

图5 噪声对Harris算法的影响

图6 噪声对S-Harris算法的影响

从图4～6可以看出：对图像进行噪声处理后，改进后的S-Harris算法相比Harris算法，检测效果较好。算法本身受噪声影响较小。表1是通过对重庆理工大学校门进行噪声处理后角点检测数量对比结果。

表1 改进的Harris算法在不同噪声强度下的识别效果

实验中，随着噪声强度的增加，Harris算法的误检概率较大，改进的S-Harris算法虽然也存在误检率，但是相比原算法，改进后效果较好。

3.2.2 角点检测时间对比

对于同一幅图像，研究角点检测所花费的总时间，以此检测S-Harris算法同Harris算法相比是否在时间消耗上进行了优化。为了能更好地突出实验效果，本实验对比过程中选择了已采用的重庆理工大学校门图，同时对图像分辨率分别进行适当的放大和缩小，在此选择300×65、450×98、675×147、1012×220、1 518×330的像素来进行实验比较。图7为在300×65像素下的实验检测效果对比。

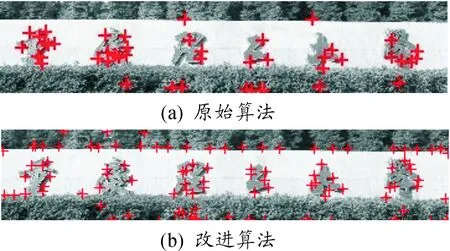
图7 300×65像素下算法对比效果

由表2可知：改进的S-Harris算法相比传统的算法，运算时间效率上得到了明显的提高，这得益于积分图像的优势。

表2 算法运算时间效率对比

4 结束语

本文提出了一种S-Harris角点检测算法，此方法针对Harris角点检测算法存在的缺陷问题，引入了自适应的灰度差分理念和积分图像的思想。前者增强了该算法的抗噪性，根据像素点领域内的对比度偏差，选取其自适应的阈值，通过实验证明该方法在不同的噪声环境下，对角点提取的准确性和精确性相比原算法都得到了较好的提高。后者则有效地降低了时间复杂度。在图像矩形特征计算中，计算出其积分图像，则可在常量时间内计算出该积分图像内部任意大小矩形区域的特征信息，不仅能降低运算量，还能提升计算机的处理能力。通过在不同的分辨率图像下的对比实验证明，利用该方法能够在不改变任何参数的前提下以及不降低角点检测的准确性的同时检测效率得到显著提升。

通过将灰度差分理念和积分图像思想相结合的方法，本文所提及的S-Harris算法不仅能在对不同噪声环境下得到有较稳定的角点检测效果，并且对于较高的图像分辨率角点检测时间也有明显的改善。未来工作中，计划在视频图像应用领域中应用该算法，进一步验证算法的有效性。