颗粒沉降问题的SPH数值模型研究

邵家儒，杨 瑜，黄志涛，邹 麟

(1.重庆理工大学 机械工程学院， 重庆 400054； 2.庆铃汽车(集团)有限公司， 重庆 400052)

在自然界和工业应用中存在很多颗粒两相流动问题，如风沙泥沙输运、污水处理、气体除尘等。在液固两相系统中，流体对固体的作用力来自压强和剪应力两方面，而该力通常受到流体的性质(密度及黏性等)、相对流速、颗粒形状等的影响[1-2]。颗粒两相流动通常呈现多态性和复杂性，涉及多相流、微流体力学等多个方面，随着研究的不断深入，颗粒两相流的内涵和外延也在不断拓展[3]。

在颗粒沉降的数值模拟研究方面，毛威等[4]采用格子Boltzmann方法模拟了热对流条件下的颗粒沉降问题，分析了不同温度下颗粒在流体中的沉降行为。Niu等[5]基于二维IB-LBM方法对二维圆形颗粒的沉降行为进行了数值模拟，发现沉降过程中领先的颗粒尾部会产生一个低压涡旋，尾随颗粒会被此尾涡捕捉，从而使其沉降速度快于领先的颗粒。Aidun等[6]使用二维格子Boltzmann方法模拟了圆柱体在充满静止流体的二维槽道中的沉降动力学行为，并在研究中发现了二维颗粒沉降的周期分岔和混沌状态。刘汉涛等[7]应用任意拉格朗日-欧拉(ALE)方法模拟了热对流条件下的颗粒沉降过程，指出热对流会引起颗粒不同的动态尾迹。已有的数值模拟研究中大多没有研究黏性、壁面与颗粒间的相互作用等因素对颗粒沉降问题的影响。

光滑粒子动力学(SPH)方法是一种拉格朗日型无网格粒子方法，在该方法中所模拟的介质(流体/结构物)用一系列的粒子来代替，每个粒子具有自身的材料属性，如质量、密度等[8-9]。在进行物理量离散的过程中，每个粒子上的物理量仅由其支持域内的粒子基于核函数插值决定。光滑粒子动力学方法非常适合研究涉及强非线性自由液面流动、流体与结构相互作用的问题，具有很好的自适应性[10-11]。本文基于光滑粒子动力学方法，引入雷诺平均湍流模型，构造了流体与结构的交界面算法，通过虚拟粒子技术解决了密度差异引起的数值震荡问题。对单颗粒、双颗粒沉降过程进行了数值模拟研究，确定了颗粒距离壁面位置、流体黏性等因素对沉降过程的影响，研究了不同颗粒间的相互作用。

1 SPH控制方程

1.1 SPH流体相控制方程

颗粒沉降问题中流体相的计算基于Navier-Stokes方程进行，描述如下[12]：

ρ▽·V

(1)

(2)

式中：ρ为密度；V为速度矢量；g为重力加速度；P为压力；μ为动力黏性系数；R为雷诺应力张量,

(3)

δab

(4)

(5)

(6)

其中：Sab为平均应变率张量；k为湍动能；υt为涡黏系数；l为混合长度，l=Csh，cs为Smagorinsky常数，本文模拟中取值为0.12。经过SPH离散后，控制方程中对应项可写为如下形式：

▽iWij

(7)

(8)

(9)

(10)

其中：mj为粒子j的质量；W为核函数；h为光滑长度；x为粒子的空间位置坐标。

任何一种不可压缩流体理论上都可以看作是具有弱可压缩性的，因此本文应用Monaghan提出的状态方程[9]进行求解，描述如下：

(11)

其中：B=c2ρ0/γ，c为人工声速，其取值通常为流场最大特征速度的10倍，这样既可以使流体的可压缩性保持在1%以下，又可以节约计算时间；ρ0为参考密度；γ=7。

1.2 SPH固体相模型

刚体上任意一点a的运动可以用式(12)进行描述。

ua=uc+uca=uc+ωc×rca

(12)

式中：uc为刚体质心的平动速度；ωc为刚体自转的角速度；rca为从刚体质心到点a的位移向量。刚体质心的平动和刚体自转的角速度可由如下方程求解：

(13)

(14)

其中：F为整个刚体受到的总的流体作用力；M为刚体的质量；Lc为刚体受到的外力对刚体质心的力矩；Ic为刚体相对于其质心的转动惯量。对固体相方程进行SPH离散得：

(15)

(16)

式中：aj为粒子j的加速度；rj为粒子j的空间位置；R0为旋转中心的位置。

2 液固交界面算法

如图1所示，固壁边界由3类固定的虚粒子构成，均匀分布在边界外，其层数由所应用核函数的支持域半径来确定，从而保证在真实粒子的支持域内不会出现粒子缺失[12]。

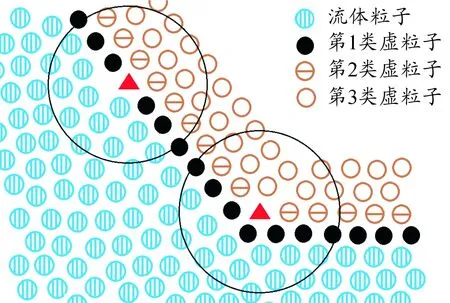
图1 流固耦合交界面模型示意图

在标准的SPH边界算法中，边界粒子被当成流体粒子直接参与相关物理量的计算。由于该方法在被截断的支持域中直接计算，导致相关物理量震荡非常剧烈，不能得到高精度的计算结果。为了恢复核函数的归一化性质，提高边界粒子相关物理量的计算精度，本文应用如下公式计算边界粒子上的相关物理量：

(17)

(18)

β0+βx(xi-xj)+βy(yi-yj)]Wij

(19)

(20)

(21)

对于颗粒沉降问题而言，固体颗粒与流体间往往存在一定的密度差异。为了消除密度差异对计算带来的影响，本文采用了虚拟粒子技术，即当支持域内存在密度不同的粒子时，采用如下公式进行计算：

(22)

该计算格式可以保证核函数的归一化性质得到满足。

3 数值算例

本文基于矩形槽道建立了颗粒沉降问题的数值模型，如图2所示。矩形槽道宽为d，高为h，内部液体初始时刻保持静止。槽道内固体颗粒半径为R，初始保持静止，因密度差异在自身重力的作用下在槽道内开始沉降。内部液体设定为水，其密度为ρf=1 000 kg/m3，颗粒的密度为ρs=1 250 kg/m3。

图2 颗粒沉降模型示意图

3.1 单颗粒中心沉降

本文首先对单颗粒的中心沉降问题进行了数值模拟。模型中动力黏性为0.01 Pa·s，颗粒半径R=0.001 25 m，槽道宽度d=0.02 m，高度h=0.06 m。

从图3中可以看到:在单颗粒中心位置沉降过程中，整个流场基本保持对称。颗粒密度与流体密度的差异使得颗粒沿重力方向运动。运动过程中产生的拖曳力带动颗粒附近流体向下运动，同时颗粒下降过程中对两侧流体的挤压使其具有向上的速度矢量，从而形成涡旋结构。随着时间的增加，颗粒的速度逐渐增加，后期在黏性阻尼力的作用下将达到一个稳定的速度。这一过程中，颗粒附近的漩涡结构逐渐变化，由于边界的影响，最后形成2个细长的漩涡结构。

图3 槽道中心位置处颗粒沉降过程

3.2 单颗粒偏心沉降

如果颗粒不从中心位置沉降，而是中心偏离对称轴一段距离，那么沉降过程中将会产生很多新的现象。这里对模型进行修改，模拟了颗粒的偏心沉降问题。模型中d=0.01 m，颗粒中心距离左侧壁面0.007 5 m。首先忽略流体的黏性作用，如图4所示。由于计算域的不对称性，刚体与刚体壁面存在两体相互作用，驱动颗粒向平衡位置运动，在颗粒运动过程中驱动周围流体从而形成尾涡，尾涡随颗粒的运动与时间的推移逐渐发展并最终脱落。由于不考虑黏性的作用，颗粒在流场中没有黏性阻尼作用，流场中复杂的涡结构使得颗粒越过平衡位置，最终与刚体壁面接触。

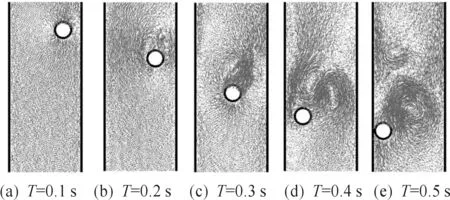
图4 无黏性单颗粒偏心沉降过程

为了进一步研究流体黏性阻尼力对颗粒的影响，这里稍微增大动力黏性至0.001 Pa·s，对单颗粒偏心沉降过程进行了新的数值模拟。可以看到：略微增大黏性后，颗粒的整个运动形态发生了很大的变化，当颗粒越过平衡位置后，由于黏性力及颗粒的两体相互作用力，迫使颗粒趋近平衡位置，使得颗粒沿对称轴摇摆着沉降。颗粒沉降路径的差异必然导致流场中涡旋结构的变化，黏性颗粒后的尾涡更加明显，作用区域也更大，如图5所示。

图5 有黏性单颗粒偏心沉降过程

3.3 双颗粒沉降

增加沉降颗粒的数目，流场中又会出现一些新的现象。本算例对双颗粒沉降问题进行了数值模拟，分析了固体颗粒间的相互作用及引起的流场变化情况。模型中颗粒的半径、密度均与本文之前算例保持一致，槽道宽度保持为0.01 m，水的动力黏性为0.001 Pa·s。该模型中两颗粒初始时刻的中心分别距离左侧壁面0.007 5、0.002 5 m，距离槽道底部分别为0.04 m和0.035 m。

图6为双颗粒沉降过程。由于初始时刻两颗粒的中心位于偏离槽道中心线±0.025 m处，颗粒在初始沉降阶段仍然会趋向于槽道中心线运动，此阶段两颗粒的相互作用并不明显，然而随着时间的增加，上方颗粒A开始进入下方颗粒B的尾涡区，出现了拖拽现象，此时两颗粒的垂直速度都明显增大，颗粒A的速度将大于颗粒B，两颗粒间的相对距离逐渐减小，最终相互接触。接触后在扭转力矩的作用下，颗粒的旋转作用十分明显，亲和后的颗粒开始分开，同时颗粒A超过颗粒B继续向下沉降，而颗粒B在扭转力矩和边界力的作用下产生了一个向上的速度。当颗粒B的动能由黏性力和漩涡作用消耗掉后又会向下继续沉降。SPH方法可以很好地模拟出双颗粒沉降问题中的DKT过程，即拖拽(drafing)、接触(kissing)与翻转(tumbling)。

图6 双颗粒沉降过程

4 结束语

本文基于光滑粒子动力学方法建立了矩形槽道内的颗粒沉降数值模型。应用雷诺平均湍流模型以及涉及密度差异的交界面算法，模拟了流场中的涡旋结构以及流体与固体颗粒间的相互作用。通过SPH模型分析可以发现：在单颗粒沉降中，颗粒的初始位置、流体的黏性对沉降轨迹有较大的影响。在双颗粒沉降中，SPH模型很好地模拟出了颗粒在黏性力、边界力作用下出现的拖拽、接触与翻转过程。