源于教材练习题的变式探究

满延福

教材中的练习题一般都具有基础性与代表性的特点，许多练习题、习题、期末测试题、中考试题均源于教材中练习题、习题的改编或变式，在教学中正确引导对原题进行适当的变式拓展，对发挥学生的潜力，将有助强化学生基础，培养学生发现问题、分析问题、解决问题的能力。现就湘教版初中数学八年级下册的一道练习题为例进行说明，本文将与读者共赏。

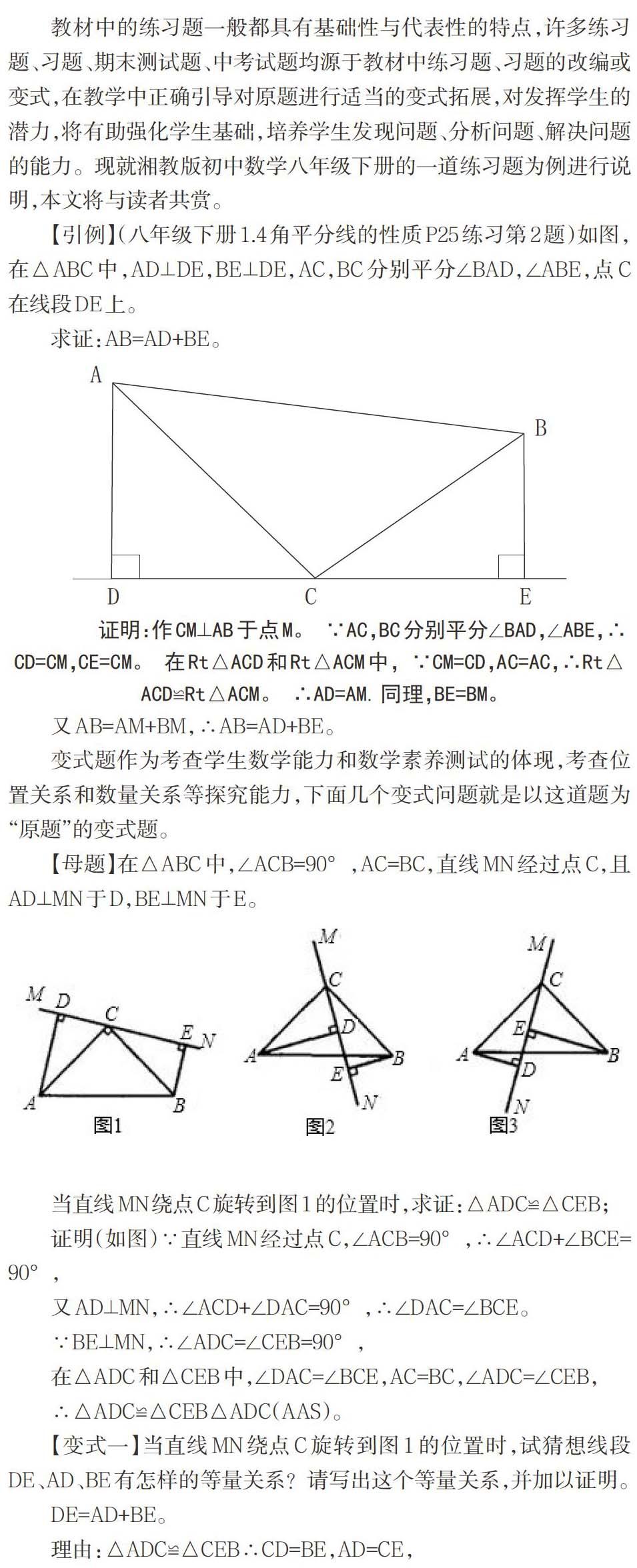
【引例】（八年级下册1.4角平分线的性质P25练习第2题）如图，在△ABC中，AD⊥DE，BE⊥DE，AC，BC分别平分∠BAD，∠ABE，点C在线段DE上。

求证：AB=AD+BE。

证明：作CM⊥AB于点M。 ∵AC，BC分别平分∠BAD，∠ABE，∴CD=CM，CE=CM。 在Rt△ACD和Rt△ACM中， ∵CM=CD，AC=AC，∴Rt△ACD≌Rt△ACM。 ∴AD=AM.同理，BE=BM。

又AB=AM+BM，∴AB=AD+BE。

变式题作为考查学生数学能力和数学素养测试的体现，考查位置关系和数量关系等探究能力，下面几个变式问题就是以这道题为“原题”的变式题。

【母题】在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E。

当直线MN绕点C旋转到图1的位置时，求证：△ADC≌△CEB；

证明（如图）∵直线MN经过点C，∠ACB=90°，∴∠ACD+∠BCE=90°，

又AD⊥MN，∴∠ACD+∠DAC=90°，∴∠DAC=∠BCE。

∵BE⊥MN，∴∠ADC=∠CEB=90°，

在△ADC和△CEB中，∠DAC=∠BCE，AC=BC，∠ADC=∠CEB，

∴△ADC≌△CEB△ADC（AAS）。

【变式一】当直线MN绕点C旋转到图1的位置时，试猜想线段DE、AD、BE有怎样的等量关系？请写出这个等量关系，并加以证明。

DE=AD+BE。

理由：△ADC≌△CEB∴CD=BE，AD=CE，

∴AD=CE=CD+DE=BE+DE。

【变式二】当直线MN绕点C旋转到图2的位置时，试猜想线段DE、AD、BE有怎样的等量关系？请写出这个等量关系，并加以证明。

DE=AD-BE。

理由：∵△ADC≌△CEB∴CD=BE，AD=CE，

∵DE=CE-CD∴DE=AD-BE。

【变式三】当直线MN绕点C旋转到图3的位置时，试猜想线段DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明。

DE=BE-AD。

理由：∵△ADC≌△CEB∴CD=BE，AD=CE，

∵DE=CD-CE∴DE=BE-AD。

一题多变，不仅可以培养学生的发散思维能力及相关知识点迁移能力，还可以大大扩大学生的知识容量，经常做这种训练，不仅可以提高学生思維质量，还可以培养学生面对难题的良好的从容心态。

新课程标准中提倡“通过解决问题的反思，获得解决问题的经验”。数学教学离不开例题习题，而教学中如何选择例题习题，从而挖掘教材潜在的智能价值，充分展示教学功能，并使课本知识有效地浓缩。通过不同角度、不同层次、不同情形、不同背景的变式，使一题多变，从而揭示不同知识点的联系，使学生加深知识的理解与内化，使知识系统化，克服某些思维定势，发散学生思维，培养学生思维的灵活性、全面性和创新性，提高学生解决实际问题和应变的能力。