支持少样本的高速滚齿工艺参数优化
曹卫东,阎春平,吴电建
(重庆大学 机械传动国家重点实验室,重庆 400044)
0 引言
近年来,滚齿加工尤其是高速滚齿加工得到了迅猛发展,其工艺更加注重加工绿色化和低碳化[1-4]。合适的工艺参数在低碳化的滚齿加工中显得尤为重要[3-5],但在实际决策、生产运用中存在诸多难题,例如在少量历史加工案例条件下,如何在得到优化工艺参数的同时满足企业对加工质量、加工成本、加工时间、环境影响等多方面的要求,其中的难点为:①作为先进技术,高速滚齿加工积累的工艺实例较少[5];②缺少合适的优化算法。因此,少样本下的高速滚齿工艺参数优化问题亟需解决。
在工艺参数优化决策领域,很多学者致力于无监督式算法研究,即不需要历史加工实例,通过建立目标与变量的数学模型,采用遗传算法、响应面分析法等求解得到优化工艺参数,这类方法在车削、铣削、钻削等领域尤为常见[6-8]。部分学者着眼于有监督式算法研究,文献[5]以工艺实例为基础,将图论作为工具分析工艺实例相似特征关联,采用模糊逼近理想排序法,以加工效果相对最优为目标对备选实例进行多属性决策,得到最优工艺参数;文献[9]提出一种新的多基因遗传规划方法,基于历史实例,以产品质量和能耗为目标进行工艺参数优化,结果显示:车削时,切削速度对能耗有着显著的影响。本文主要针对有监督式算法,文献[5]的方法能够寻找到最相似实例,但仍需要人工进行后续参数修正。基于支持向量回归(Support Vector Regression, SVR)的参数优化方法[10-11]为解决上述问题提供了一个较好的思路。SVR在较少样本下具有突出的优势[12],但需要设置较多参数,包括核函数类型、惩罚因子和松弛变量等,将多目标蜻蜓算法(Multi-Objective Dragonfly Algorithm, MODA)[13]加入,可以优化支持向量回归初始设定参数,使SVR具备更强的泛化能力。具体方法为建立高速滚齿加工效果评价模型,计算包括齿向方向误差、齿形方向误差、齿面粗糙度、加工时间、加工成本、碳耗在内的目标值,运用MODA寻找非支配解(SVR设定参数),利用SVR生成工艺参数组,再次利用高速滚齿加工效果评价模型计算工艺参数的目标值,循环上述过程,得到ε-SVR参数和工艺参数非支配解集,即优化ε-SVR参数组和工艺参数组,所得的工艺参数组能够满足企业多样化的需求。本文方法能够支持高速滚齿工艺参数少样本优化决策,具有一定优势。
1 问题描述
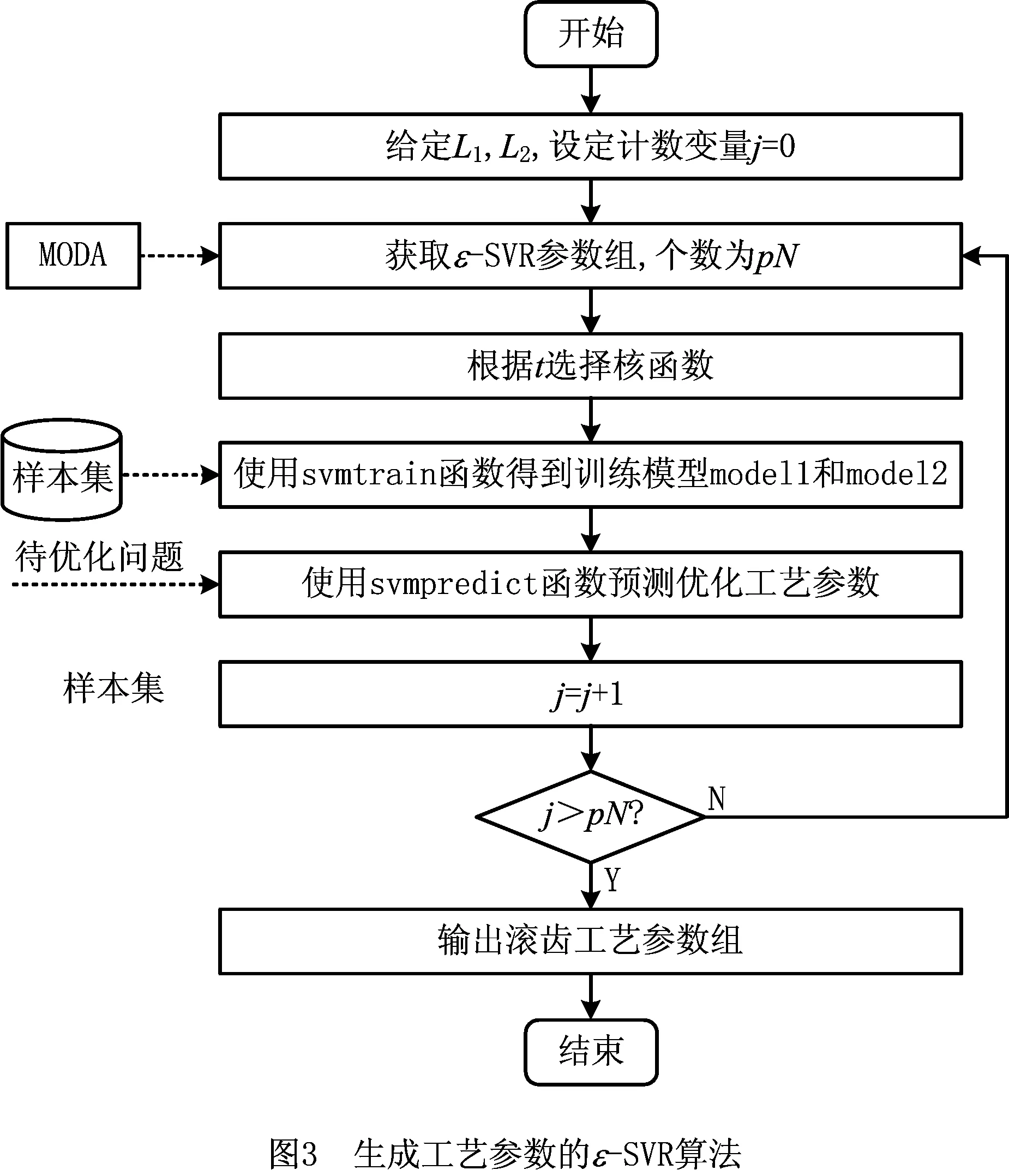
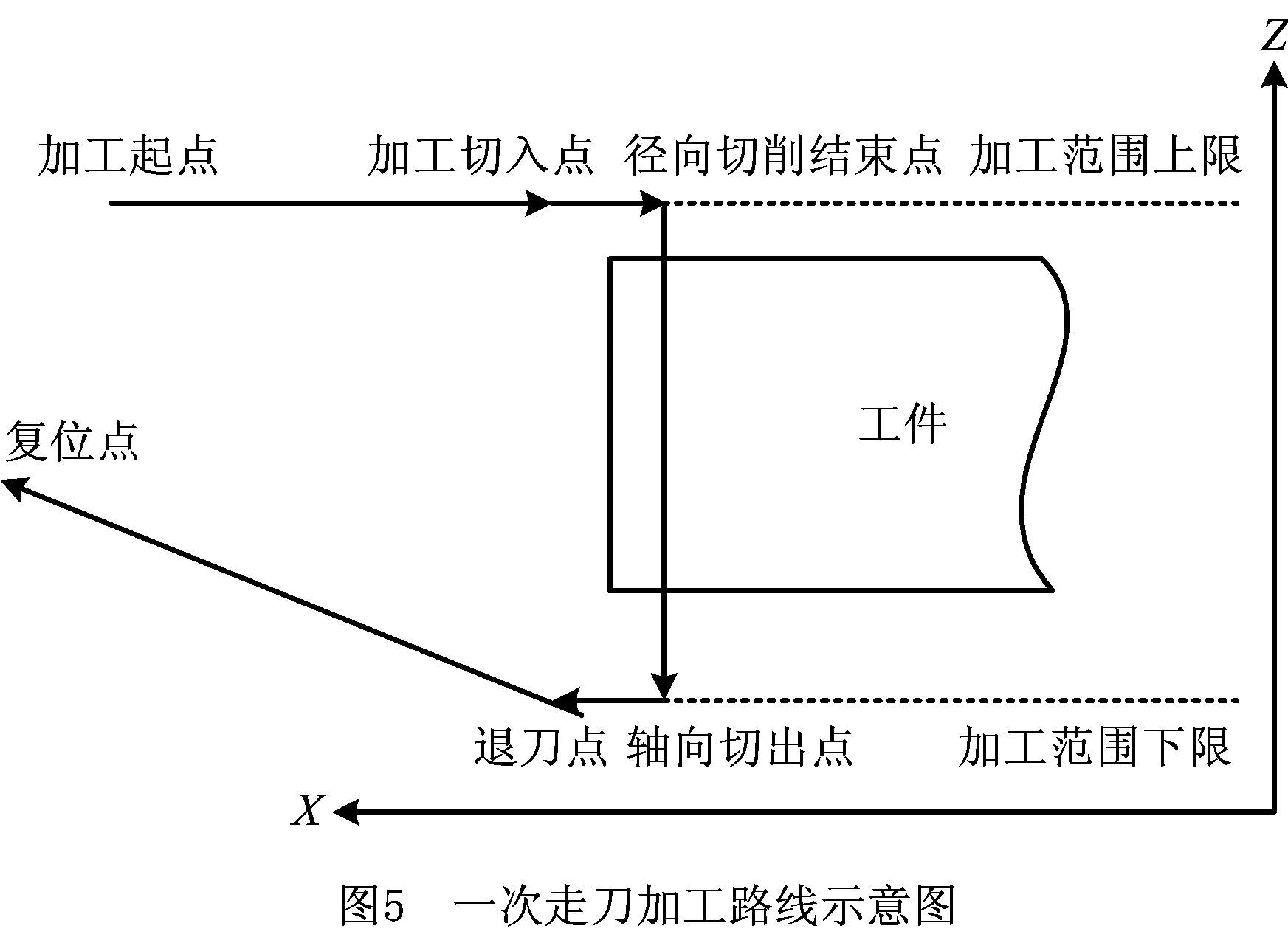
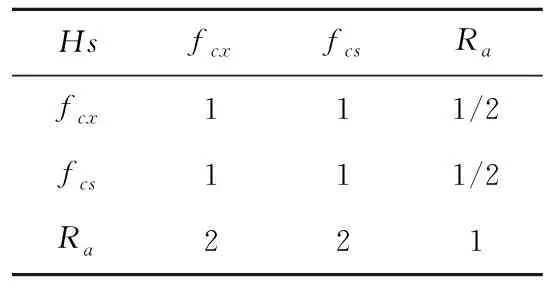
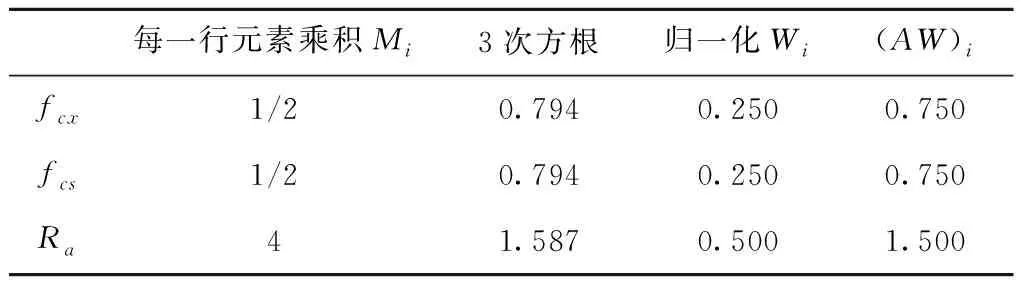
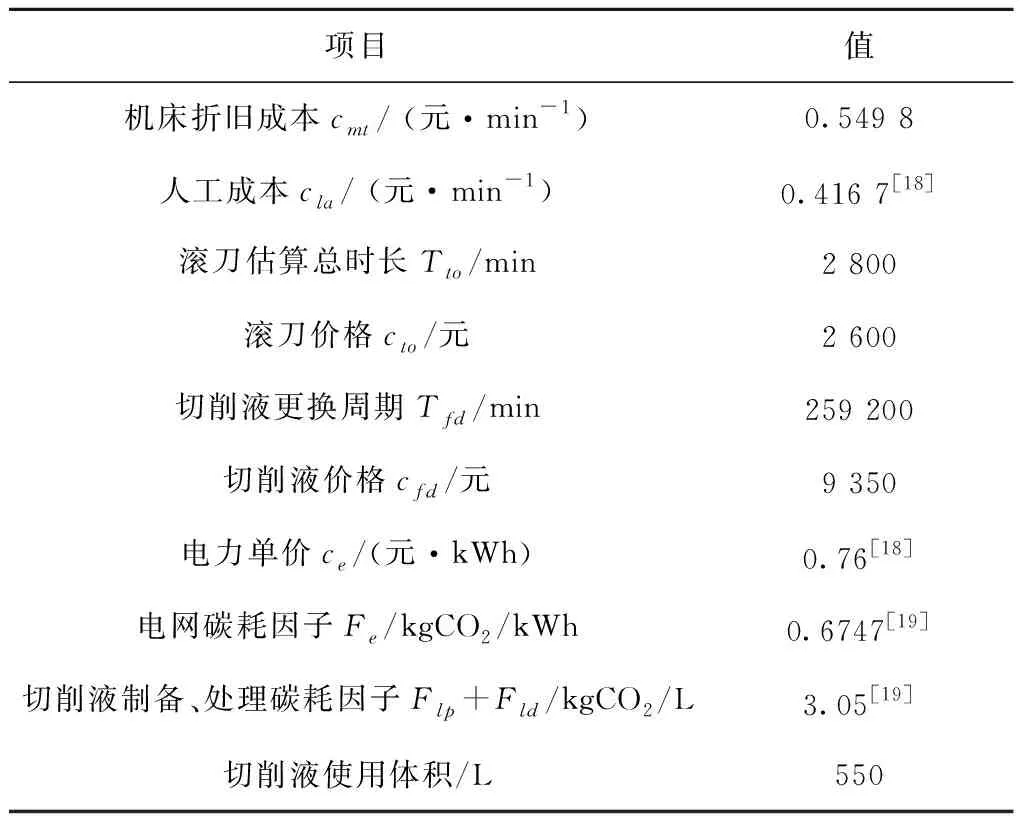
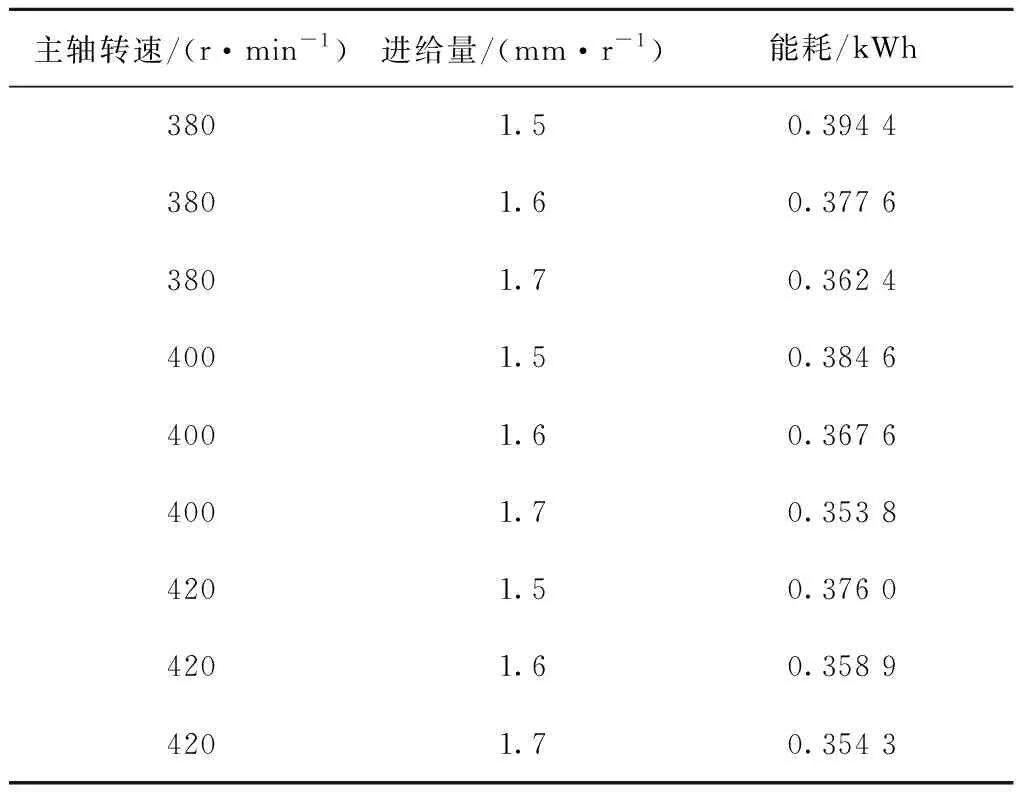
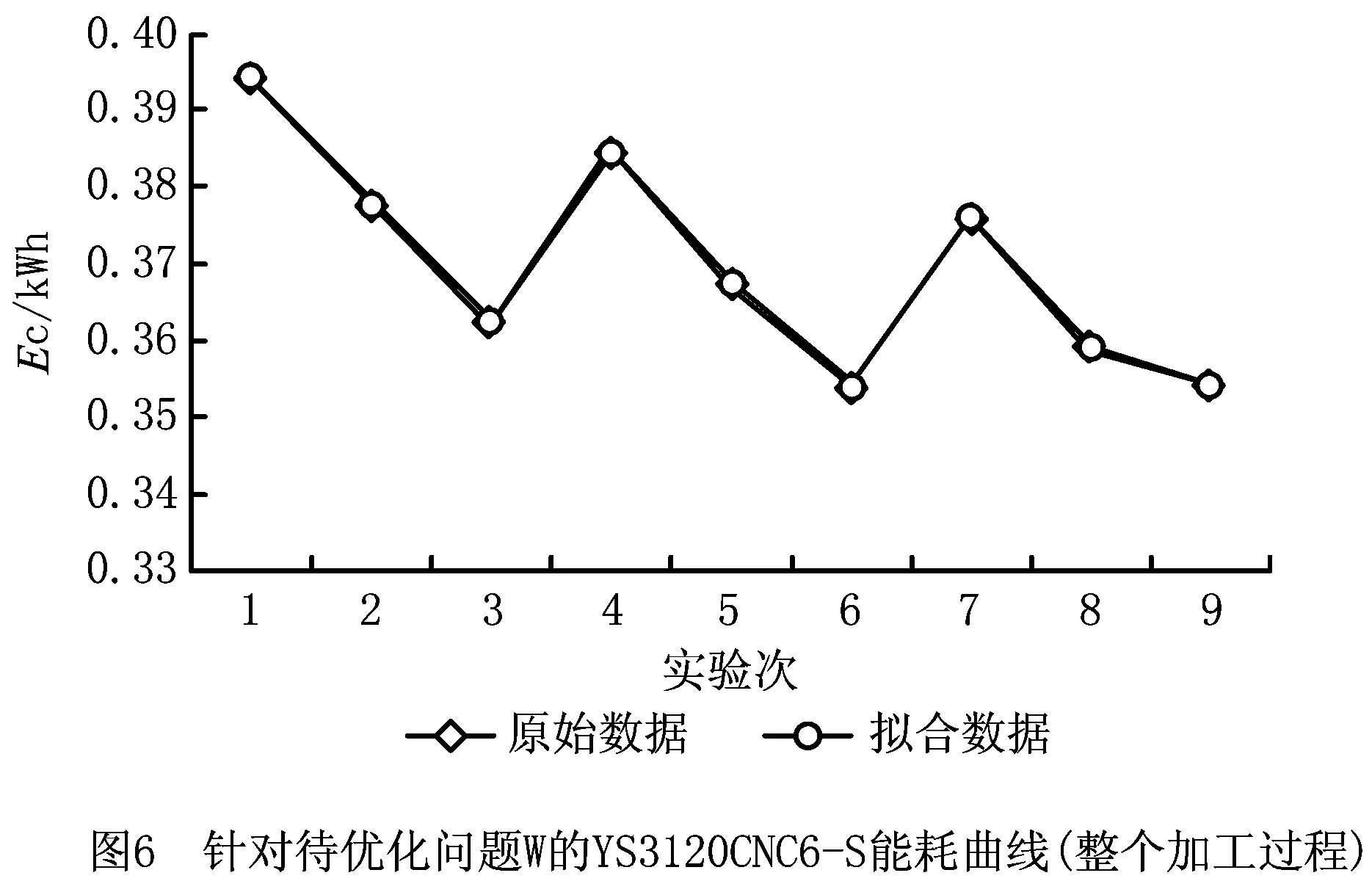
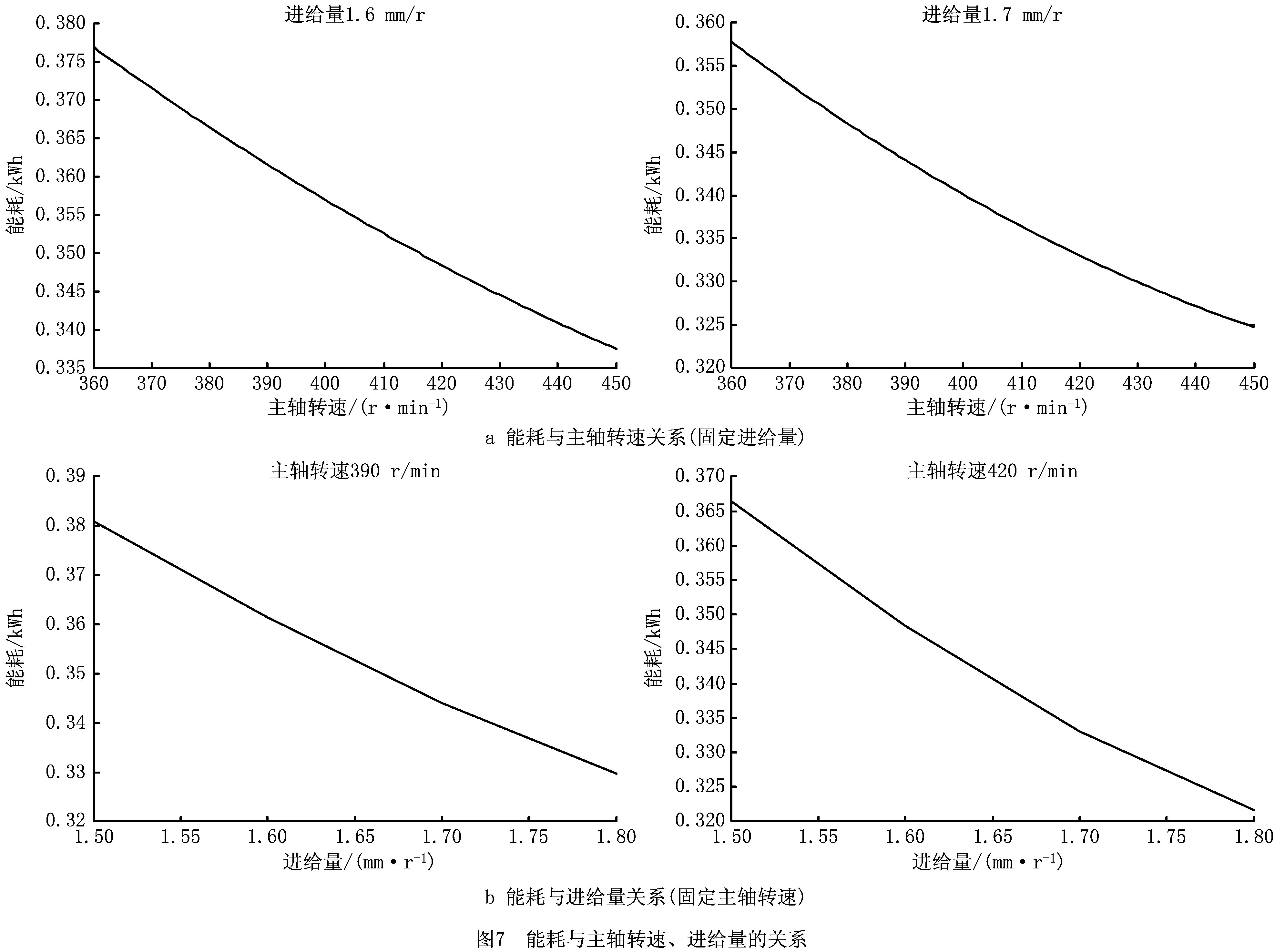
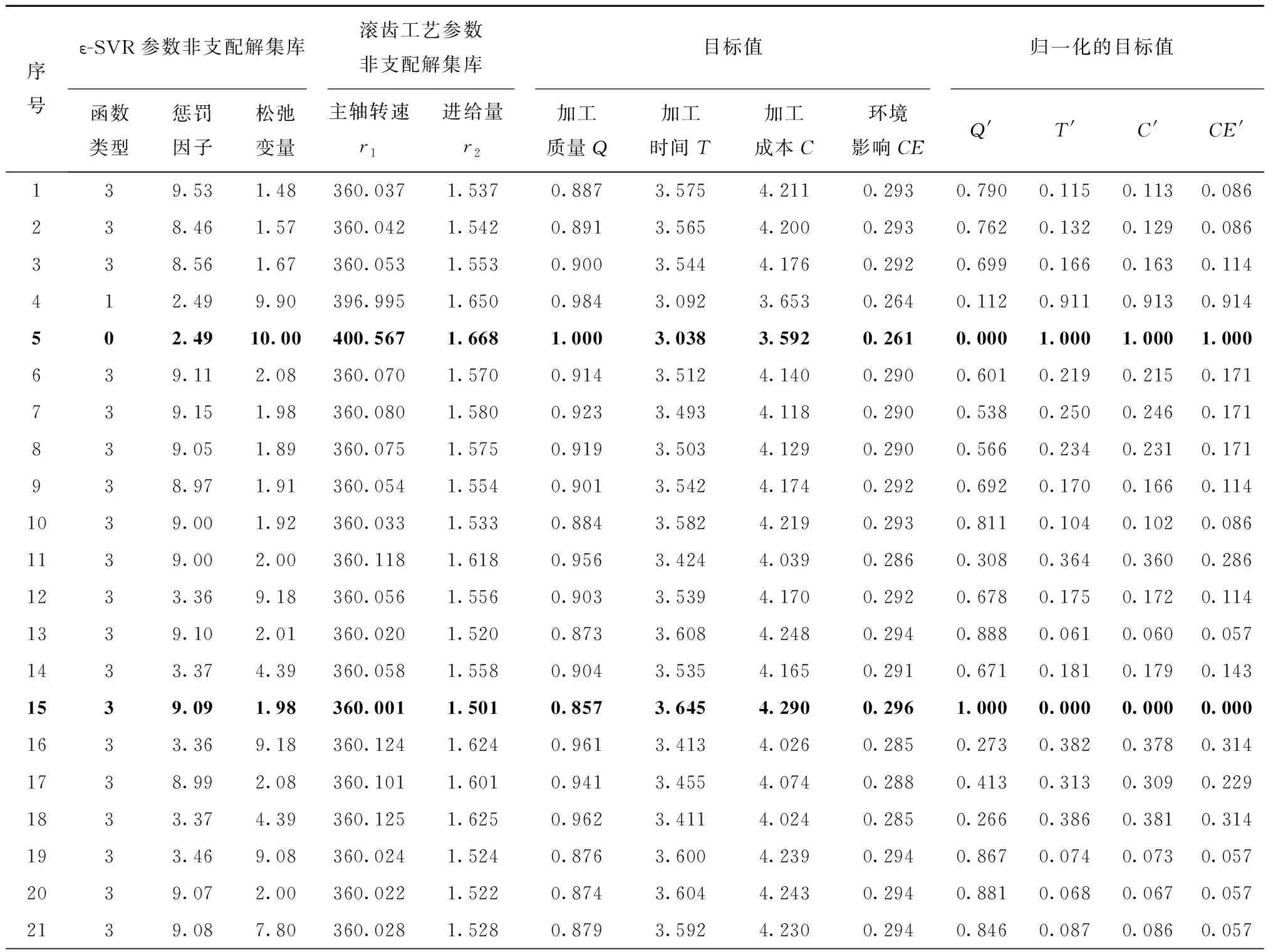
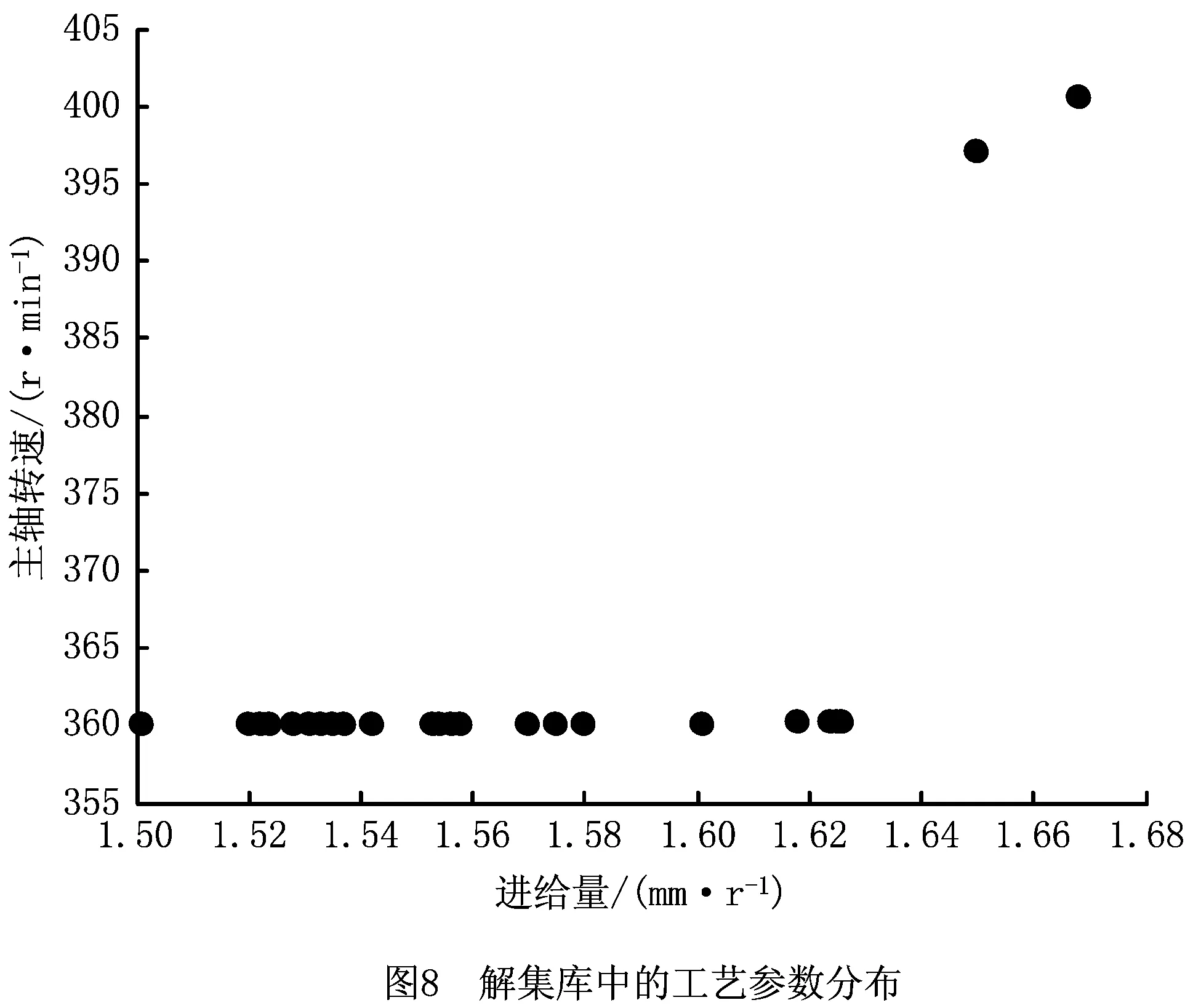
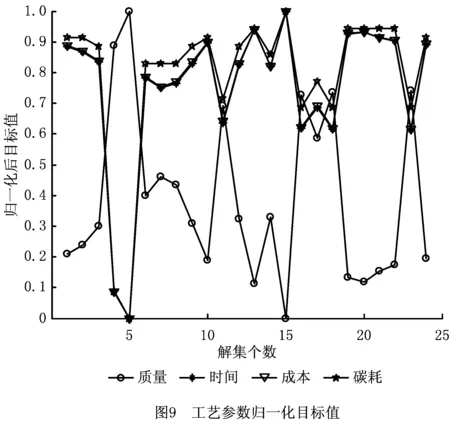
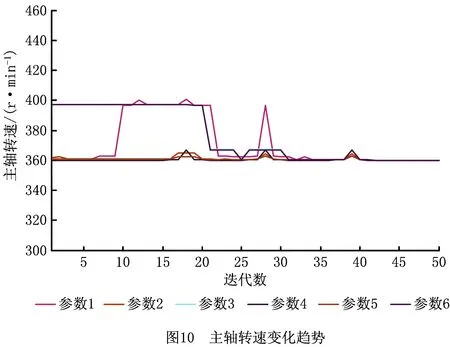
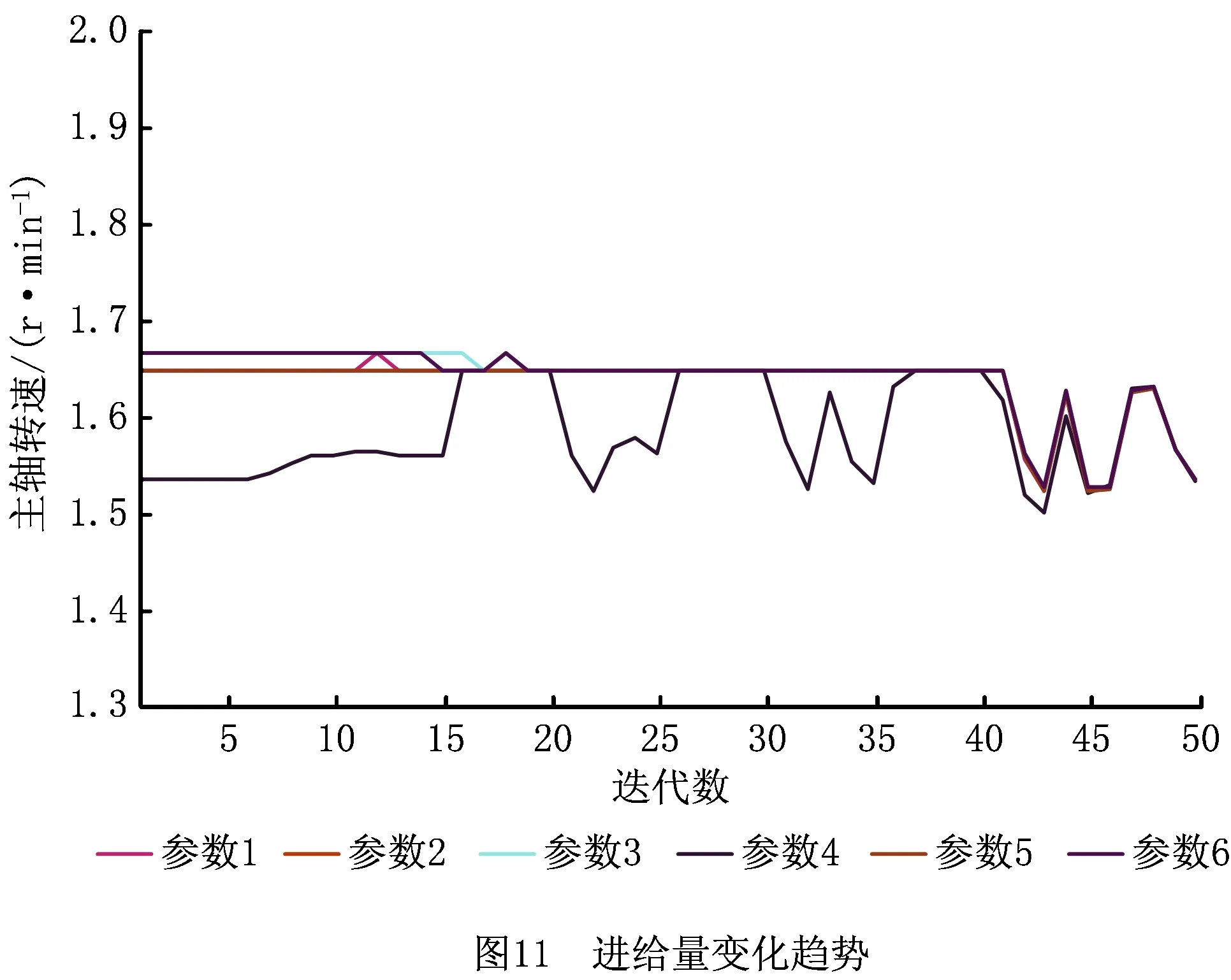
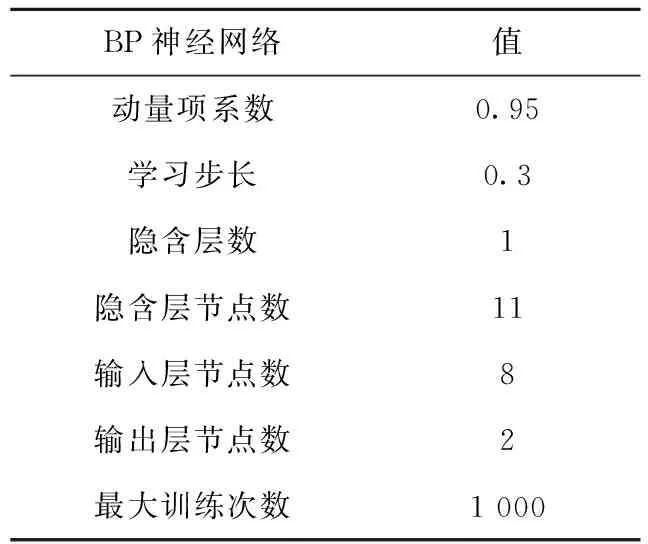
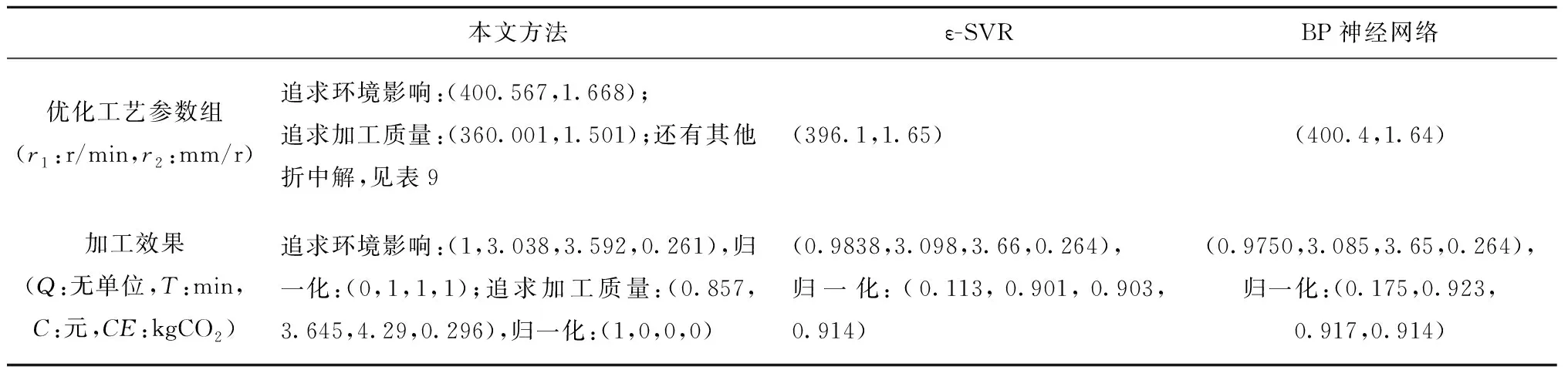
将少样本的高速滚齿工艺参数优化问题记为Q=(W,L)[5],其中:W={fa1,fa2,…,fan1}为待优化工艺问题,L={l1,l2,…,lm}为样本集,样本li={{fai,1,fai,2,…,fai,n1},{ri,1,ri,2,…,ri,n2}},f为问题属性,r为决策结果属性,m,n1,n2为正整数,m 表1 问题属性及决策结果属性 为了量化加工效果,选用加工质量、加工时间、加工成本和环境影响作为评价要素,建立滚齿加工效果评价模型,如图1所示。选用齿向方向误差、齿形方向误差、齿面粗糙度评价加工质量;选用滚刀从加工起点开始到回到复位点结束的整个时间评价加工时间;选用机床折旧费用、人工费用、滚刀费用、切削液费用、电力费用计算加工成本;选用切削加工碳耗和切削液评价环境影响。 依据上述模型,建立本文优化目标函数F(r1,r2)={Q,T,C,CE}[5],定量计算方法为:加工质量Q中评价项有齿向方向误差、齿形方向误差和齿轮表面粗糙度[14-15],先分别除以各项极限值,再通过层次分析法[16]确定权重,最后通过加法运算得到加工质量。公式如下: (1) 式中:wq1,wq2,wq3分别为齿向方向误差、齿形方向误差和齿轮表面粗糙度的权重,由层次分析法确定;fMcx,fMcs,RMa分别为齿向方向误差、齿形方向误差和齿轮表面粗糙度的极限值,由于本文的加工质量是越小越好,fMcx,fMcs,RMa应取各项计算结果的最大值;j为滚刀槽数,ra为刀尖圆弧半径。 加工时间T通过切削时间、快速进给时间、慢速进给时间求和得到[17], (2) 式中:ΔH为切入行程,E为切出行程,FaDis为快速进给行程,FaSpeed为快速进给速度,SlDis为慢速进给行程,SlSpeed为慢速进给速度。 加工成本C通过机床折旧费用、人工费用、滚刀费用、切削液费用、电力费用求和得到[18]。其中:机床折旧费用是机床单位时间的折旧成本cmt与加工时间的乘积;人工费用是工人单位时间的报酬cla与加工时间的乘积;滚刀费用是滚刀价格cto在使用总时长Tto中的分摊;切削液费用是切削液价格cfd在更换周期Tfd中的分摊;电力费用是制造过程能耗Ec与其单价公式ce的乘积,Ec的计算公式通过重庆大学刘飞课题组研发的能够适应高速滚齿机床的机床多源能耗状态信息在线检测系统[20]采集历史能耗数据拟合得到。因此 C=Cmt+Cla+Cto+Cfd+Ce (3) (4) 2.2.1 支持少样本的高速滚齿工艺参数优化框架 支持少样本的高速滚齿工艺参数优化方法如图2所示,步骤如下: 步骤1设定MODA最大迭代数,ε-SVR参数组内个数、ε-SVR参数非支配解集库的长度、滚齿工艺参数非支配解集库的长度。 步骤2初始化ε-SVR参数组(核函数类型、惩罚因子和松弛变量)。 步骤3利用ε-SVR参数组,以样本集为训练数据,通过ε-SVR算法计算出多个滚齿工艺参数组(主轴转速、进给量)。 步骤4运用高速滚齿加工效果评价模型对每组工艺参数进行评价,使用Pareto最优法求解得滚齿工艺参数非支配解集及对应的ε-SVR参数非支配解集,解集个数为rN。 步骤5当ε-SVR参数非支配解集库大于自身长度时,随机删除rN个解,将新解加入非支配解集库。 步骤6从ε-SVR参数非支配解集库中随机选择一个“食物源”(可能解)和一个“天敌”(不可能解)。 步骤7利用MODA的分离、对齐、内聚、食物吸引、天敌排斥等公式计算新的ε-SVR参数组。 步骤8如果不大于最大迭代数,则转步骤3,否则终止计算,得到ε-SVR参数非支配解集库和滚齿工艺参数非支配解集库,即优化ε-SVR参数组和优化工艺参数组。 步骤9根据企业实际需求,进行滚齿加工。 需要注意的是,虽然用Pareto最优得到的解集不一定能够让目标Q,T,C,CE同时达到最优,但是能够在某种程度上反映Q,T,C,CE之间的特性,企业可以根据自己实际需求选择相应的优化工艺参数进行加工。 2.2.2 支持生成工艺参数的支持向量回归(ε-SVR) SVR的标准形式在文献[21]首次提出,软件LIBSVM[22]有该方法的具体实施过程。本文选用ε-SVR生成滚齿工艺参数(主轴转速、进给量),ε-SVR的初始设定参数包括核函数类型、惩罚因子和松弛变量,本文的ε-SVR算法过程如图3所示,具体步骤如下: 步骤1给定训练样本集L1={(x1,z1,1),…,(xm,zm,1)},L2={(x1,z1,2),…,(xm,zm,2)},其中xi∈Rn,xi的属性为fa1,fa2,…,fa8;zi,1,zi,2∈R1,zi,1的属性为r1,zi,2的属性为r2,i=1,…,m,计数变量j=0。 步骤2获取MODA生成的ε-SVR参数(核函数类型t、惩罚因子c和松弛变量p),其个数为pN,SVR的其他参数设定取默认值[23]。 步骤3根据t选择核函数K(x,x′)。 步骤4使用LIBSVM中的svmtrain函数分别训练L1,L2,得到训练模型model1(关于r1)和model2(关于r2)。 步骤5针对待优化问题W,利用model1和model2,使用LIBSVM中的svmpredict函数分别预测得到优化工艺参数。 步骤6j=j+1。 步骤7若j>pN,则终止计算,输出优化工艺参数组,否则转步骤2。 核函数K(xi,xj)=φ(xi)φ(xj)可以是任意满足Mercer条件的对称函数。4种经典核函数在文献[22-23]中有详细介绍,本文利用MODA优化核函数的选择,不需要人工选定。 (1)线性核函数K(xi,xj)=xi·xj。 (2)多项式核函数K(xi,xj)=[γ(xi·xj)+β]d。 (3)径向基核函数K(xi,xj)=exp(-γ|xi-xj|2)。 (4)sigmoid核函数K(xi,xj)=tanh(γ(xi·xj)+β)。 2.2.3 多目标蜻蜓算法 受到自然界蜻蜓捕食和躲避天敌的启发,Mirjalili[13]研发出一种元启发式算法——蜻蜓算法[13],并在此算法的基础上增加Pareto最优法,列出了MODA。与NSGA-Ⅱ相比,MODA表现出了更好的收敛性及泛化能力,与多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization, MOPSO)性能相当。本文借鉴并修改MODA以优化ε-SVR初始参数,最终达到了优化工艺参数的目的。 (1)MODA具体步骤 具体步骤如下: 步骤1初始化ε-SVR参数组(蜻蜓种群)Xi(i=1,2,…,n)。 步骤2初始化步长向量ΔXi(i=1,2,…,n)。 步骤3设定超球体的最大个数。文中ε-SVR参数为3个,故围绕参数的是一个球体,其作用为ε-SVR参数组具备n个球体,距离相近的参数的球体之间会相互交叠,当解集库满时,会除去被球体密集覆盖的ε-SVR参数或选为不可能解(平衡机制);被球体覆盖稀疏的ε-SVR参数,会被选为可能解。 步骤4设定ε-SVR参数非支配解集库的长度和滚齿工艺参数非支配解集库的长度。 步骤5调用ε-SVR算法得到滚齿工艺参数组,用滚齿加工效果评价模型计算每个工艺参数对应的目标值。 步骤6利用Pareto最优得到滚齿工艺参数非支配解集及对应的ε-SVR参数非支配解集,解集个数为rN。 步骤7如果ε-SVR参数非支配解集库已满,则运用平衡机制删除rN个非支配解集库里的解。 步骤8将新的解集加入ε-SVR参数非支配解集库,同时将对应的工艺参数存入滚齿工艺参数非支配解集库。 步骤9如果新增的ε-SVR参数解集不在现有超球体范围内,则更新超球体以覆盖新的解集。 步骤10运用轮盘赌算法从ε-SVR参数非支配解集库的最稀疏区域选择一个可能解X+。 步骤11运用轮盘赌算法从ε-SVR参数非支配解集库的最密集区域选择一个不可能解X-。 步骤12寻找邻居个数N,邻居位置V,计数变量k=0。 步骤14设计数变量k1=0。 rinte为[0,1]之间的一个数。 步骤16k1=k1+1。 步骤17如果k1<3,则转步骤15。 步骤18k=k+1。 步骤19如果k 步骤20检查新的解集是否在设定的范围内。 步骤21如果不满足终止条件,则转步骤5;否则终止计算,得到ε-SVR参数非支配解集库和滚齿工艺参数非支配解集库,可根据企业对质量、时间、碳耗等目标的要求,选择适当的工艺参数进行加工。 (2)Pareto最优 在多目标问题中,对于目标评价有两种方法比较常见:①为各个目标设定权重,用专家评价、层次分析方法等求解权重,将多目标转化为单目标问题求解[5];②利用Pareto最优、改进方法均衡各目标,以获得多组非支配解(帕累托前沿),减少因人工干预目标而带来的优化结果偏差。本文选用第②种方法,4个关键术语描述如下[13,24-25]: 1)Pareto改进 设定两个向量x=(x1,x2,…,xk),y=(y1,y2,…,yk)。x优于y(xy)当且仅当 ∀i∈{1,2,…,k}:fi(x)≤fi(y)∧ ∃i∈{1,2,…,k}:fi(x) (5) 2)Pareto最优 一个解x∈X能被称为Pareto最优当且仅当 {y∈X|yx}。 (6) 3)Pareto最优集 Pareto最优解的集合称为Pareto最优集(非支配解集): Ps:={x,y∈X|yx}。 (7) 4)Pareto前沿 包含目标函数值的Pareto最优集称为Pareto前沿: Pf:={f(x)|x∈Ps}。 (8) 实验设备:①数控高速滚齿机YS3120CNC6-S搭载西门子840D数控系统,该机床为某公司最新研发的六轴四联动智能高速滚齿机,最高转速可达1 200 r/min,最大加工模数为6 mm;②齿坯;③计算机;④机床多源能耗状态信息在线检测系统(LDMS)[20];⑤MATLAB软件。实验基本步骤为:用本文方法生成工艺参数,通过本课题组研发的滚齿数控编程软件[26]自动生成数控代码,发送到数控系统,经工艺人员确认无误后进行加工,加工现场如图4所示。 待优化工艺问题W={2,0.349,41,0.456,94.011,13,71,1}。种类为渐开线圆柱齿轮,材料为20CrMo,刀具为TiAlN涂层滚刀,加工精度为7级,准备50个齿坯,采用逆滚轴向进给方式加工。加工路线如图5所示,样本选择条件为:①具备与待优化工艺问题相同的机床、工件种类、工件材料、加工刀具、进给方法及加工精度;②利用实例相似度公式[27]计算样本与待优化工艺问题接近程度,相似度范围为0~1,越接近1,样本与待优化工艺问题接近程度越高,规定实例相似度要在0.9以上。依据选择条件得到最终样本集,容量m=7,具体数据与实例相似度值(如表2)为 (9) 式中:X,Y表示两个实例,xi表示实例X中第i个元素,yi表示实例Y中第i个元素,nXY表示实例中元素的个数。 表2 高速滚齿工艺样本集 序号优化问题决策结果fa1fa2fa3fa4fa5fa6fa7fa8r1r2待优化问题之间的相似度L12.4500.401460.436128.5513.508033601.50.918L21.8900.288390.57693.5513.708023601.80.937L31.8140.286470.579106.2218.007034501.50.929L42.0000.307450.550109.6813.807034101.50.965L52.0000.346530.463123.2013.207034101.50.997L62.5000.401260.00072.0014.158023601.80.915L72.0000.340210.53254.3016.908023601.80.992 3.2.1 针对案例的高速滚齿加工效果评价模型 (1)关于加工质量 针对待优化工艺问题W,加工时间、加工成本、环境影响中的内部元素都能转化为以唯一单位表示的数值,进行加法运算;对加工质量内部因素(齿向方向误差、齿形方向误差和齿轮表面粗糙度)进行主次要分析,利用层次分析法中的层次单排序求得wq1,wq2,wq3,目标Hs为取得加工质量内部权重,准则层为齿向方向误差、齿形方向误差和齿轮表面粗糙度,不需要方案层。组织重庆某大型机床和齿轮制造企业相关专家,利用层次分析法中的要素比较判断尺度表给出判断矩阵,如表3所示。 表3 判断矩阵A 进行层次单排序,得到准则层对目标层的层次排序,如表4所示。 表4 准则层对目标层的层次排序 最大特征根λmax=3.000,一致性指标CI=0,执行性比例CR=0<0.1,CR满足要求,判断矩阵具有满意一致性,按照Wi分配权重,得wq1=0.25,wq2=0.25,wq3=0.50。 关于极限值fMcx,fMcs,RMa,事先不能确定齿向方向误差、齿形方向误差和齿轮表面粗糙度的最大值,需要设定3个全局极限值,每次迭代运算时取fcx,fcs,Ra各自的最大值,并与上一代进行比较,不断更新这3个参数。滚刀槽数为14,刀尖圆弧半径为0.6 mm,结合式(1),得到针对待优化工艺问题W的加工质量计算公式 (10) 式中Q为各评价项比值的和,无单位。 (2)关于加工时间 切入行程ΔH=24.846 mm,切出行程E=4.861 mm,快速进给行程FaDis=138.860 mm,快速进给速度FaSpeed=800 mm/min,慢速进给行程SlDis=10 mm,慢速进给速度SlSpeed=90 mm/min。结合式(2),得到针对待优化工艺问题W的加工时间计算公式 (11) 式中T的单位为min。 (3)关于加工成本 针对待优化工艺问题W,加工成本中各类已知成本如表5所示。 表5 加工效果评价中的参数设定 表6 YS3120CNC6-S能耗数据 结合式(3),得到针对待优化工艺问题W的加工成本 C=1.092 8T+0.76(-23.311 83+ 0.090 874r1+23.669 64r2-0.081 318r1·r2- (12) 式中C的单位为元。 (4)关于环境影响 电网碳排放因子、切削液制备的碳耗因子、切削液处理的碳耗因子、切削液使用体积如表5所示,得 到针对待优化工艺问题W的环境影响 CE=0.674 7(-23.311 83+0.090 874r1+ (13) 式中CE的单位为kgCO2。 利用待优化工艺问题W的基础参数和加工质量、加工时间、加工成本及环境影响的计算公式,得到各目标值,利用Pareto最优方法寻求非支配解。另外,本文存在4个优化目标,属于高目标优化问题,现给出加工时间T与环境影响CE的关系来证明高速滚齿工艺参数优化问题可以使用基于Pareto机制的算法进行求解。结合图1中加工时间T的公式及ΔH,E,fa6等定值,可知T与r1,r2都成反比;结合图1中环境影响CE的公式、上文中Ec的公式,在表2给出主轴转速范围(360~450)、进给量范围(1.5~1.8),运用MATLAB绘制相应曲线,部分曲线如图7所示,可知CE与r1,r2都成反比。综上,加工时间T与环境影响CE成正比关系。 3.2.2 针对案例的高速滚齿工艺参数优化决策 初始化ε-SVR参数组,初始设定参数如表7所示。将表2中的样本集代入2.2.2节介绍的ε-SVR算法,生成初始工艺参数组:参数1(360.792,1.65),参数2(360.960,1.65),参数3(397.084,1.668),参数4(360.036,1.536),参数5(362.031,1.65),参数6(397.082,1.67)。 运用加工效果评价模型进行评价,得到初始滚齿工艺参数非支配解集(360.036,1.536),(362.031,1.65)。 表7 初始参数设定 续表7 迭代50次后,得到ε-SVR参数非支配解集库和滚齿工艺参数非支配解集库,如表8所示。工艺参数分布范围如图8所示,文中的加工质量、加工时间、加工成本及环境影响都是越小越好,利用归一化公式[6]对各目标值进行处理,处理之后1表示最优,0表示最差,以便观察各目标值间的关系,归一化公式如式(14)所示,工艺参数对应的目标值范围如图9所示,主轴转速变化趋势如图10所示,进给量变化趋势如图11所示。迭代完后确定的极限值fMcx=0.003 35,fMcs=0.000 21,RMa=0.149。 (max.xi(n)-min.xi(n))。 (14) 式中max,min分别表示求向量x的最大值和最小值。 表8 ε-SVR参数非支配解集库和滚齿工艺参数非支配解集库 续表8 以非支配解1为例,在切削参数(360.037,1.537)的条件下,归一化目标值分别为0.790,0.115,0.113,0.086。可以看出,在该切削参数条件下,加工质量最为重要(比重71.55%),其次分别为加工时间(比重10.44%)、加工成本(比重10.25%)、环境影响(比重7.76%),企业根据适合的比重选择切削参数,本文方法给企业带来较大的选择空间。 从表8和图9可以看出,加工质量Q与其他目标成反比关系,即加工质量Q最优时,其他目标最差,如非支配解15;加工时间T、加工成本C、环境影响CE同时达到最优时,加工质量Q最差,如非支配解5;同时也存在大量折中解。企业可以根据自己对目标的需求,选择相应的工艺参数。如某企业比较重视环境影响,则可选择非支配解5,理论加工效果为Q:1,T:3.038 min,C:3.592元,CE:0.261 kgCO2;实际加工效果为Q:0.992,T:3.133 min,C:3.696元,CE:0.262 kgCO2,每项误差控制在3%以内,验证了该方法的可行性。 观察表8的滚齿工艺参数非支配解集库和表2的高速滚齿工艺样本集后发现:滚齿工艺参数非支配解集库中的参数值全部在高速滚齿工艺样本集决策结果范围内,故从某种程度上,样本决定了非支配解的范围及分布。另一方面,这一现象从侧面反应了本文案例样本选择是正确的,即样本中存在有用信息。 针对3.2节中的案例,本文方法与ε-SVR(训练条件如表7)、BP神经网络算法(训练条件如表9)进行对比实验,结果如表10所示。根据3.2节,让加工质量、加工时间、加工成本、环境影响4个目标同时达到最优是困难甚至是不可能的,单独的ε-SVR算法及BP神经网络算法虽然能够对少样本案例进行计算,但一次运行只能得到一组工艺参数,不能满足企业对目标的不同需求,且在少样本的情况下,这两种方法多次生成时,结果差距较大,较难保证加工效果;本文方法能够得到多组优化工艺参数,满足企业的不同需求,且在少样本的情况下结果差距较小,能够保证加工效果,因此本文方法在少样本的情况下具备优势。 表9 BP神经网络训练条件 表10 实验结果对比 针对少量历史加工案例支撑下的工艺参数优化问题,本文选用加工质量、加工时间、加工成本和环境影响作为评价要素,建立由齿向方向误差、齿形方向误差、齿面粗糙度、加工时间、加工成本、制造过程碳耗、切削液等组成的高速滚齿加工效果评价模型,以少量样本为基础,融合MODA和ε-SVR算法,优化了ε-SVR的设置参数,核函数类型、惩罚因子和松弛变量,生成了由主轴转速、进给量组成的优化工艺参数组(非支配解集)。实验结果表明,很难找出一个工艺参数能让所有优化目标同时达到最优。文中以企业更加注重环境影响为例,给出了理论加工效果,与实际滚齿加工作比较,目标误差控制在3%以内,验证了该方法的可行性;与其他算法的比较实验验证了该方法在少样本情况下的有效性,同时本文产生的优化工艺参数组能够满足企业对优化目标的不同需求,本文为解决少样本高速滚齿工艺参数优化决策提供了一条有效途径。下一步将对工艺路线与加工工艺参数之间的影响规律进行分析,形成更加全面的滚齿加工工艺参数优化方法。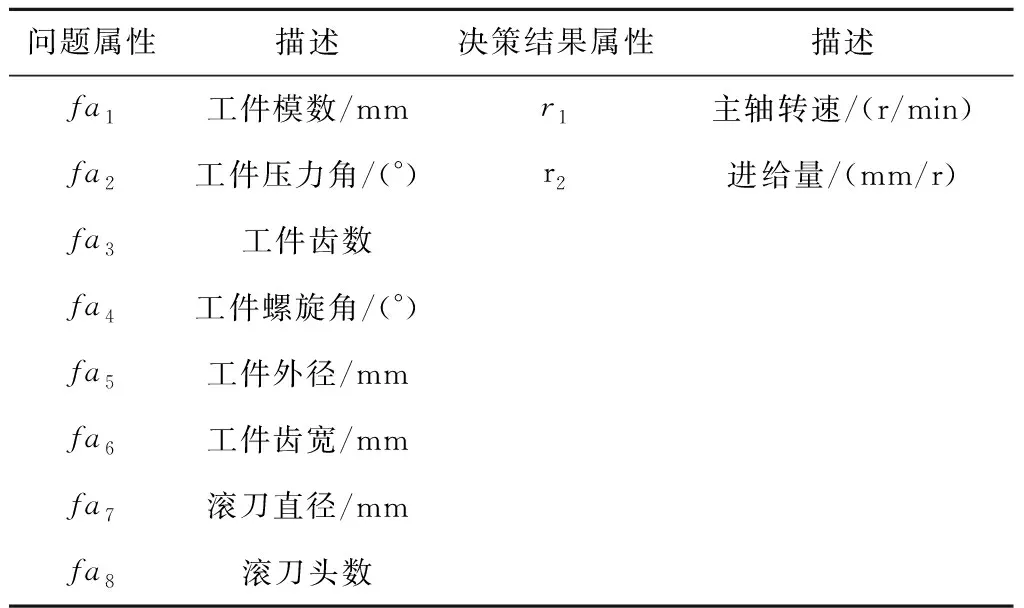
2 高速滚齿工艺参数优化
2.1 高速滚齿加工效果评价模型
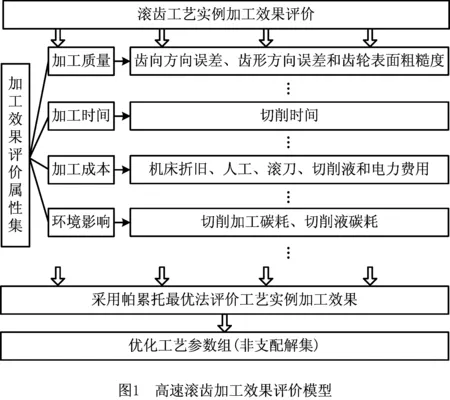
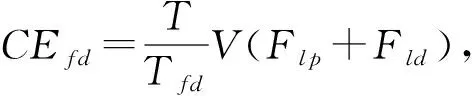
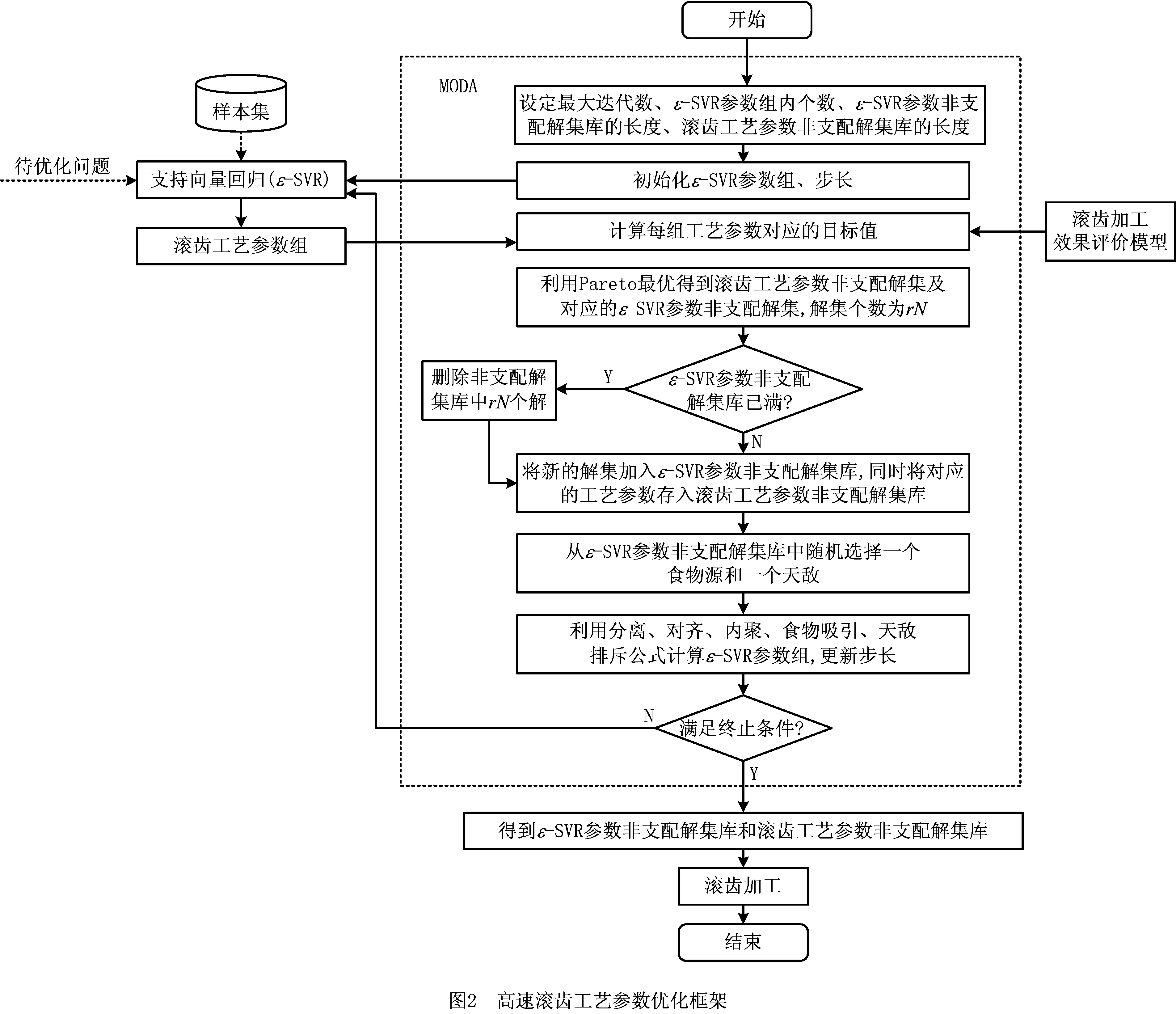
2.2 高速滚齿工艺参数优化
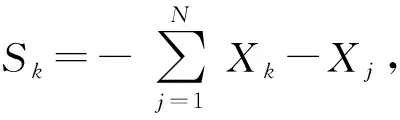
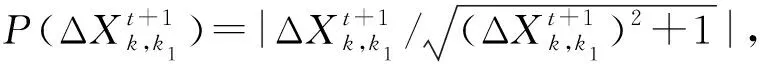
3 实例验证
3.1 实验描述

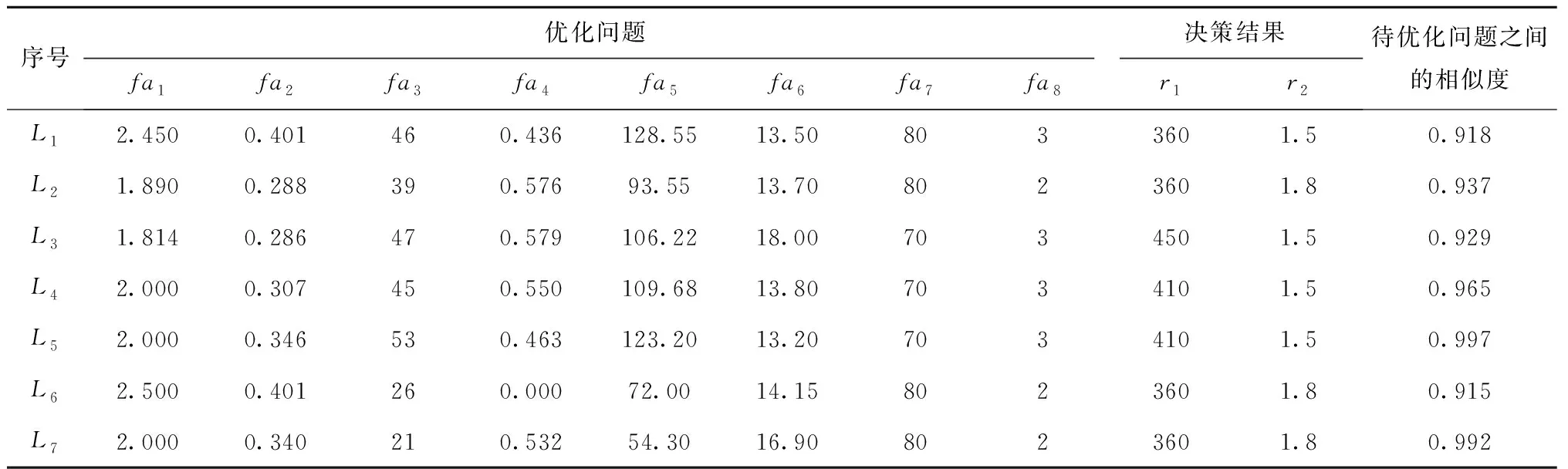
3.2 可行性验证实验
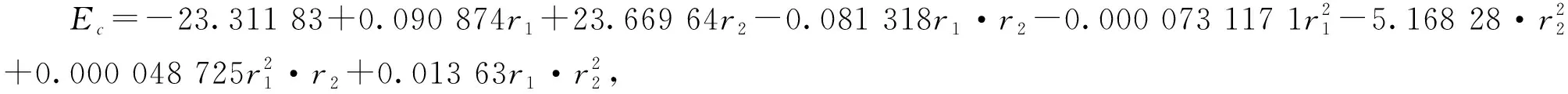
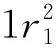



3.3 对比验证实验
4 结束语

