考虑潮汐影响的连续泊位和岸桥集成调度
郑红星,张敬涛,刘保利
(大连海事大学 交通运输管理学院,辽宁 大连 116001)
0 引言
在集装箱码头中,泊位分配、岸桥分配和岸桥调度直接影响码头的作业效率和船舶的在港时间,它们之间的集成调度是港口调度的核心问题之一;随着船舶的大型化,在水深条件受限的港口中,潮汐对泊位和岸桥集成调度的影响越来越明显。
国内外学者对集装箱码头的泊位和岸桥集成调度问题进行了较为深入的研究,按集成调度的内容可分为以下几类:第一类为泊位分配和岸桥分配问题(Berth Allocation Problem-Quay Crane Assignment Problem, BAP-QCAP),第二类为岸桥分配和岸桥调度的集成(Quay Crane Assignment Problem-Quay Crane Scheduling Problem, QCAP-QCSP),第三类为泊位分配和岸桥调度的集成(Berth Allocation Problem-Quay Crane Scheduling Problem, BAP-QCSP),第四类为泊位分配、岸桥分配和岸桥调度的集成(Berth Allocation Problem-Quay Crane Assignment Problem-Quay Crane Scheduling Problem, BAP-QCAP-QCSP)。
在BAP-QCAP的文献中,Zhang等[1]考虑岸桥的移动范围,以在港作业停泊时间成本和偏离成本之和最小为目标,构建了混合整数规划模型,并设计了对应的优化算法;乐美龙等[2]针对连续泊位和岸桥分配集成调度问题,在考虑泊位偏移和岸桥干扰因素的基础上,以船舶在港停泊时间最短为目标,构建了混合整数规划模型,并提出两阶段算法用于求解;Hu等[3]在解决泊位与岸桥分配问题时,以船舶在港的燃油消耗与气体排放量为优化目标,构建多目标混合整数规划模型,给出了线性化过程,并采用CPLEX求解;Li等[4]针对连续泊位的泊位分配和岸桥分配问题,考虑岸桥的服务范围,以船舶早到费用、延迟离泊成本、岸桥作业成本和其他相关成本之和最小为优化目标,构建了非线性混合整数规划模型,并设计了启发式算法求解;Shang等[5]在考虑岸桥启动成本的前提下,针对系统的随机性,以船舶在港作业时间与抵港等待作业时间的加权和最小为目标,构建了鲁棒优化模型,并分别设计了遗传算法和嵌入式启发式算法求解模型;He[6]在目标函数上考虑了能源消耗,兼顾作业时间与能源节约,求解最优的泊位分配与岸桥分配方案。
在研究QCAP-QCSP的文献中,Diabat等[7]以船舶作业时间最短为目标,构建混合整数规划模型,并设计了遗传算法,求解岸桥分配与岸桥调度;Fu等[8]以作业量最大化为目标,综合考虑岸桥的安全距离、集装箱装卸次序、船舶优先级等约束,构建了数学模型,并设计了遗传算法求解;Fu等[9]在文献[8]的基础上,采用拉格朗日松弛方法求解数学模型。
在研究BAP-QCSP的文献中,Liang等[10]以船舶作业时间、等待时间与延误时间最短为目标,构建数学模型,并设计嵌入启发式规则的遗传算法求解模型;Lee等[11]以所有船舶作业时间最小化与单船作业时间最小化为目标,构建两个混合整数规划模型,分别求泊位分配与岸桥调度的最优解,并设计了相应的遗传算法。
在研究BAP-QCAP-QCSP的文献中,Meisel[12]在船舶分配岸桥组保持不变的假设下,进行集成调度研究。Meisel等[13]提出一个三阶段的框架解决泊位—岸桥分配—岸桥调度问题;Türkoullar[14]在文献[12-13]的假设下建立了混合整数规划模型,并通过割平面法从BACAP(berth allocation and quay crane assignment (number) problems)的可行解中构造出BACASP(berth allocation and quay crane assignment (specific) problems)的可行解;Türkoullar[15]在Türkoullar[14]的基础上,将BACASP问题分解为主问题和子问题,结合使用分枝定界法、割平面法和动态规划法解决该问题。
综上,国内外有关泊位—岸桥集成调度的文献中,BAP-QCAP的文献最多,是此类研究的热点之一,而针对QCAP-QCSP和BAP-QCSP的研究较少;针对BAP-QCAP-QCSP的研究近年来逐年增多,是当前相关研究的焦点。就BAP-QCAP-QCSP的现有文献而言,大多以船舶在港时间或延误时间最短为优化目标,并设计相应的启发式算法求解,但考虑潮汐影响的文献较少,很多都未提及作业岸桥的具体任务序列。而在实际生产中,由于港口水深条件的限制,大吨位的船舶必须在涨潮时才能通过航道进入泊位卸船,可能也需在涨潮期间离港,即“乘潮作业”,若忽略此因素,即使得到了最优的调度方案,也无法在实际生产中实施。区别已有文献,本文的重点如下:
①考虑潮汐对连续泊位分配与岸桥调度的影响;②考虑岸桥的动态分配,即问题研究不再基于每艘船舶所分配岸桥数固定的假设;③深入考虑岸桥调度,即不仅给出每台岸桥在各时间窗服务的船舶,还给出对应的具体作业贝位;④专注于连续泊位分配、岸桥分配和岸桥调度之间的反馈关系,进而构建相互关联的多个数学模型。
本文问题可描述为:在预知抵港船舶的相关信息后,以计划期内的所有抵港船舶为研究对象,侧重某些大船需乘潮进出的特殊约束,兼顾岸桥工作时不可跨越和保持安全距离等作业约束,考虑岸桥可跨船调度的现实,研究计划期内连续泊位分配、岸桥分配和岸桥调度的集成优化,最终给出每台岸桥的作业时刻表、每艘船舶的具体泊位位置和起止时刻。
1 数学模型
基于问题特点,本文构建了一个主模型和两个子模型。其中:主模型用于求解泊位分配与岸桥分配问题;两个子模型均用于求解岸桥调度问题,子模型1求解每个时间窗岸桥服务的具体船舶,子模型2求解每艘船舶作业时岸桥装卸的时间窗和具体贝位。3个模型通过参数传递与约束关联的方式进行集成。子模型1的目标函数值为主模型的目标函数与约束的构成部分,通过主模型求得每艘船舶的具体靠泊位置与时间,以及分配的岸桥数,作为子模型1的输入,求解子模型1,再将子模型1的目标函数值回代到主模型,如此反复,可求得两个模型的集成最优解。通过求得的最优解,针对每艘船舶,整理出该船舶在泊时各岸桥的作业时间窗,作为子模型2的输入,求得每艘船舶作业期间岸桥的装卸贝位与时窗。
1.1 主模型
(1)假设条件
1)泊位为连续型泊位,水深条件相同。
2)每艘船舶的预计到港时间与最晚离港时间已知。
3)船舶均按时到港。
4)船舶的装载量、任务贝位已知。
5)每艘船舶都有其最优靠泊位置,实际靠泊位置偏移会导致作业费用增加。
6)每艘船舶都有其最大装卸岸桥数和最小装卸岸桥数。
7)岸桥作业速度相同且不变。
8)船舶靠泊离泊时间不计。
9)港口潮汐规律为最低潮时间与最高潮时间相差6 h,每天的涨潮时间相隔0.8 h。
(2)相关参量
V为船舶集合;
Vp1为需要乘潮进港的船舶集合;
Vp2为需要乘潮出港的船舶集合;
L为泊位长度;
T为时间单元集合;
Tp为距离0时刻最近的涨潮时刻;
K为岸桥集合;
Ka为岸桥总数;
li为船舶i的长度;
ETAi为船舶i的预计到达时刻;
ETBi为船舶i的预计离泊时刻;
wi为船舶i的装卸量;
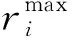
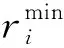
α为多台岸桥干扰系数;
f1为单位泊位偏移成本;
f2为单位时间滞期费成本;
p为岸桥装卸速度(箱/时);
M为充分大的正数。
(3)决策变量
bi为船舶i的实际靠泊位置(以船头计);
SBi为船舶i的开始作业时刻;
EBi为船舶i的结束作业时刻;
ΔTi为船舶i的滞期时间,考虑船舶滞期的最长时间为max{0,EBi-ETBi};
θ为岸桥移动成本;
(4)目标函数
(1)
s.t.
bi+li≤L∀i∈V;
(2)
∀j∈T;
(3)
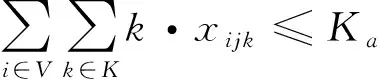
(4)
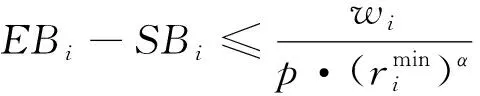
(5)

(6)
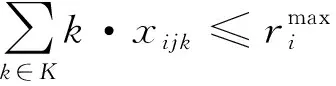
(7)
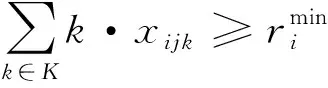
(8)

(9)
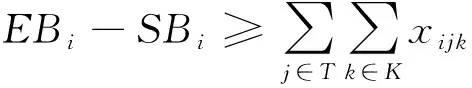
(10)
SBi≥ETAi∀i∈V;
(11)
M(1-yij)+bj≥bi+li+1∀i,j∈V;
(12)
M(1-zij)+SBj≥EBi+1∀i,j∈V;
(13)
SBi=Tp+12n1+12.8n2∃n1,n2∈N,
0≤n2-n1≤1,i∈Vp1;
(14)
EBi=Tp+12n1+12.8n2∃n1,n2∈N,
0≤n2-n1≤1,i∈Vp2;
(15)
(16)

1.2 子模型1
通过求解主模型可以得到泊位分配与岸桥分配的解,将其作为已知量构建子模型1,求解岸桥调度问题。在已知每个时刻靠泊船舶所分配岸桥数的前提下,引出时段的概念:以任意船舶分配岸桥数发生变化的时刻为界,一个时段表示前后两界之间的时刻集合。在一个时段内,每艘船舶分配的岸桥数保持不变。
(1)假设条件 ①岸桥之间无法跨越;②岸桥移动成本与岸桥移动距离成正比;③船舶的分配岸桥数已知;④船舶的靠泊位置已知;⑤岸桥初始位置已知。
(2)参数N为岸桥数量;Vt为t时段泊位上的船舶集合;T为时段集合;K为岸桥集合;di为i船舶的靠泊位置;qi为i船舶分配的岸桥数;li为船舶i的长度;c为岸桥移动单位距离所需的成本;s为岸桥间的安全距离。
(3)决策变量
wit为岸桥i在t时段的位置;

(4)目标函数
(17)
s.t.
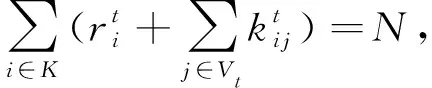
(18)
∀t∈T,∀i∈K;
(19)
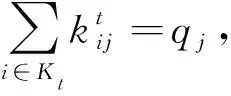
(20)
wit-wjt≥s,∀t∈T,∀i,j∈K。
(21)
其中:式(17)表示岸桥移动成本最小为目标;式(18)表示空闲岸桥与作业岸桥之和等于总岸桥数;式(19)表示岸桥在某一时刻只能服务于一艘船舶;式(20)计算任意时刻每艘船舶所分配的岸桥数;式(21)表示任何时刻岸桥均需保持安全距离。
1.3 子模型2
(1)假设条件 ①岸桥的移动速度恒定,不考虑加减速;②岸桥装卸速度恒定,各岸桥装卸速度相同;③不考虑船舶装卸过程中的平衡;④装卸贝位与装卸量已知;⑤每艘船舶所分配的岸桥已知。
(2)参数K为执行任务的岸桥集合;B为需要装卸的贝位集合;tk为第k台岸桥开始执行任务的时间;wi为第i个贝的任务量;p为岸桥装卸速度;li为第i个贝的位置;m为岸桥移动速度;M为充分大的正数。
(3)决策变量
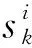
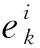
emax为所有岸桥结束任务的时间的最大值。
(4)目标函数
minz=emax。
(22)
s.t.
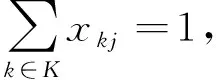
(23)
∀k∈K;
(24)
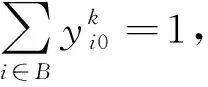
(25)

(26)
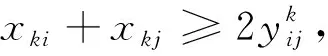
(27)
∀i∈B,∀k∈K;
(28)
∀i,j∈B,∀k∈K;
(29)

(30)
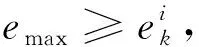
(31)
其中:式(22)表示目标函数为岸桥装卸任务完成时间最小;式(23)表示任意一个贝位只能由一台岸桥执行任务;式(24)~式(25)表示每个岸桥有唯一起始作业贝位和终止作业贝位;式(26)表示岸桥作业的连续性;式(27)为岸桥作业次序约束;式(28)计算岸桥的结束作业时间;式(29)计算岸桥的起始作业时间;式(30)表示岸桥的起始作业时间要晚于岸桥的可用时间;式(31)表示所有岸桥结束任务时间应大于等于任意一台岸桥结束任务的时间。
2 算法
2.1 算法概述
针对模型相互关联的特点,设计三阶段的混合遗传算法进行模型求解。总体思路为:令f1为主模型目标函数中去除θ的部分,f2为子模型1的目标函数,令F1(f1),F2(f1,f2)分别作为遗传算法一二阶段的适应度函数。在遗传算法的第一阶段求解主模型,得到泊位分配—岸桥分配的解,作为第二阶段的初始化种群;第二阶段设计群组分割算法,求解子模型1,得到岸桥调度的解,从而求得f2,构造适应度函数F2(f1,f2),设计遗传算法进行求解;第三阶段,通过一二阶段求得的泊位分配、岸桥分配与岸桥调度解,作为子模型2的参数,调用CPLEX规划求解器,求得具体的岸桥调度方案。算法流程图如图1所示。

2.2 算法步骤
模型与算法的映射关系如图2所示。遗传算法中,双层染色体编码的第一层与第二层染色体分别对应主模型中的决策变量靠泊位置与岸桥分配数;在编码策略中,通过约束编码的取值范围来满足主模型中的靠泊位置约束与最大最小服务岸桥数约束。靠泊时间生成算法用于求解决策变量靠泊时间,并使解集满足主模型的靠泊时间约束、潮汐时刻约束及靠泊时间空间不重叠约束。算法的适应度函数由主模型的目标函数与罚函数构成,其中罚函数用于体现主模型中的泊位总长度约束与岸桥总数量约束。

群组分割算法中,子模型1的决策变量:每台岸桥任意时间窗所服务船舶编号,转化为决策变量任意时间窗的空闲岸桥,进而转化为动态规划法中的决策变量。而岸桥组分割的方法,使得算法中的解能够满足岸桥安全距离与不可跨越约束。动态规划法中的阶段指标对应子模型1的目标函数。
算法步骤如下:
(1)染色体编码与初始种群生成
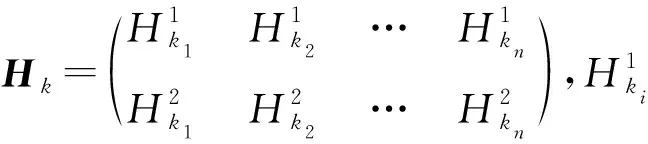
(2)生成靠泊时间
染色体的适应度基于主模型的目标函数,第一阶段的目标函数为泊位偏移成本与滞期费成本之和最小,记为f1。为计算滞期费成本,首先计算船舶的靠离泊时间。针对主模型中约束(12)与(13)、船舶靠泊的空间时间约束,以及约束(14)与(15)、潮汐时间窗约束,设计如下船舶靠泊时间算法:
步骤1按照先到先服务的原则生成乘潮进出泊位的大型船舶列表Vb={Vb1,Vb2,…,Vbm},列表大小为m。令i=1。
步骤2令船舶Vbi的到港时间为ei,靠泊时间为ti,装卸时间为hi,离泊时间为si,最近涨潮时间为em。令n=1。
步骤3若船舶Vbi与船舶Vbi-n有重叠靠泊位置且si-n>em,则ti=en,en为大于si-n与ei的最近涨潮时间;否则,ti=em。若船舶需在涨潮时离泊,则si=en,en为大于(ti+hi)的最近涨潮时间;否则,si=ti+hi。
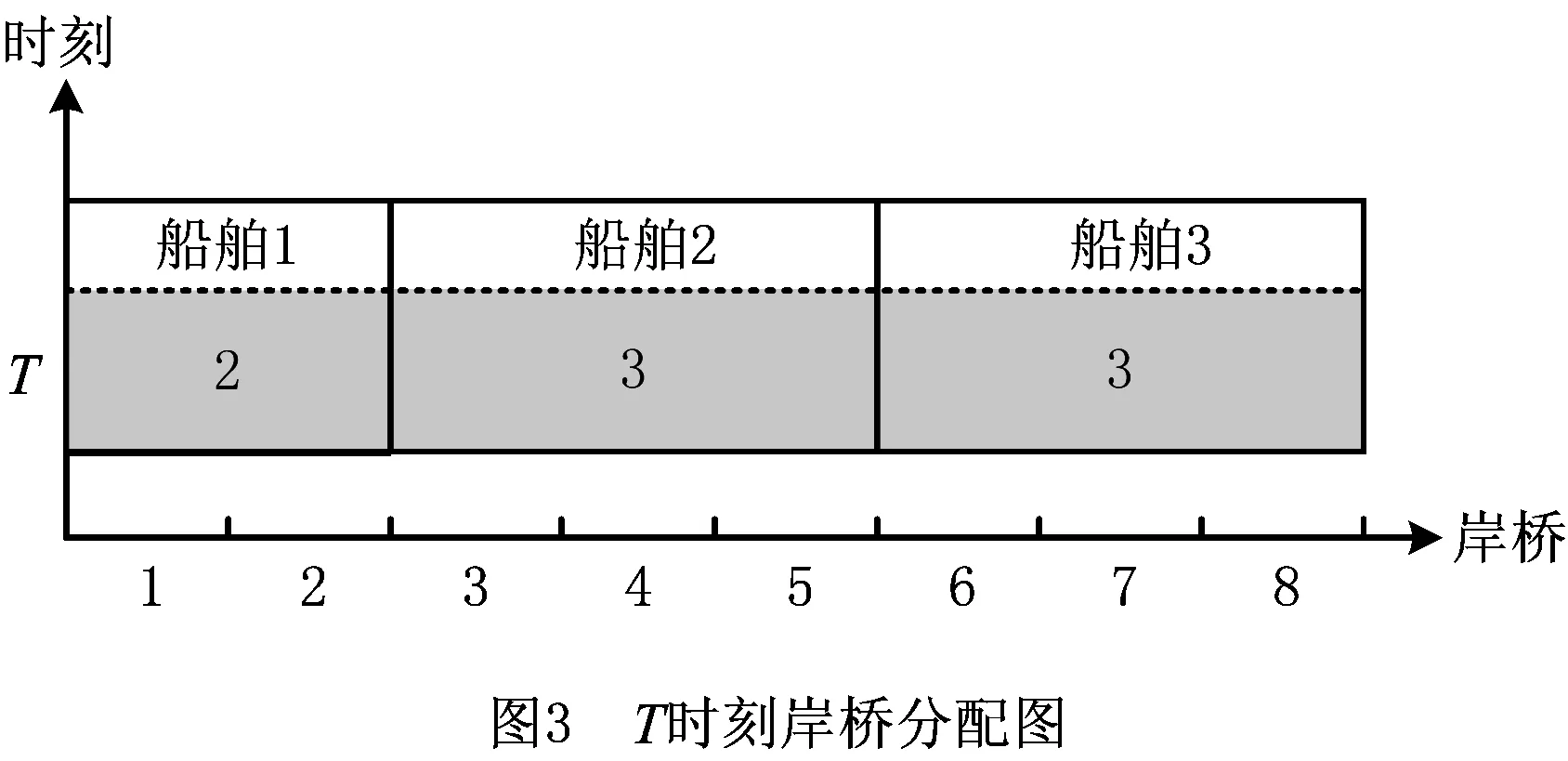
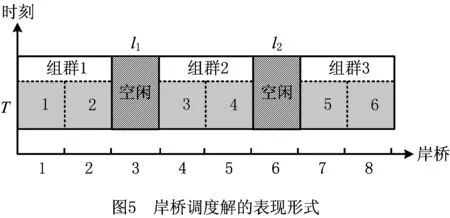
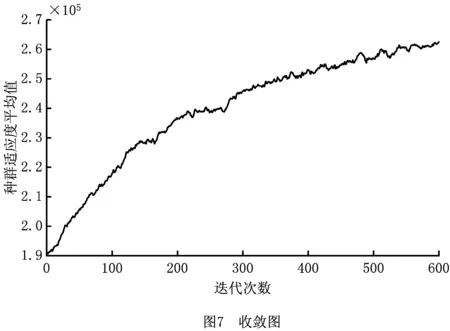
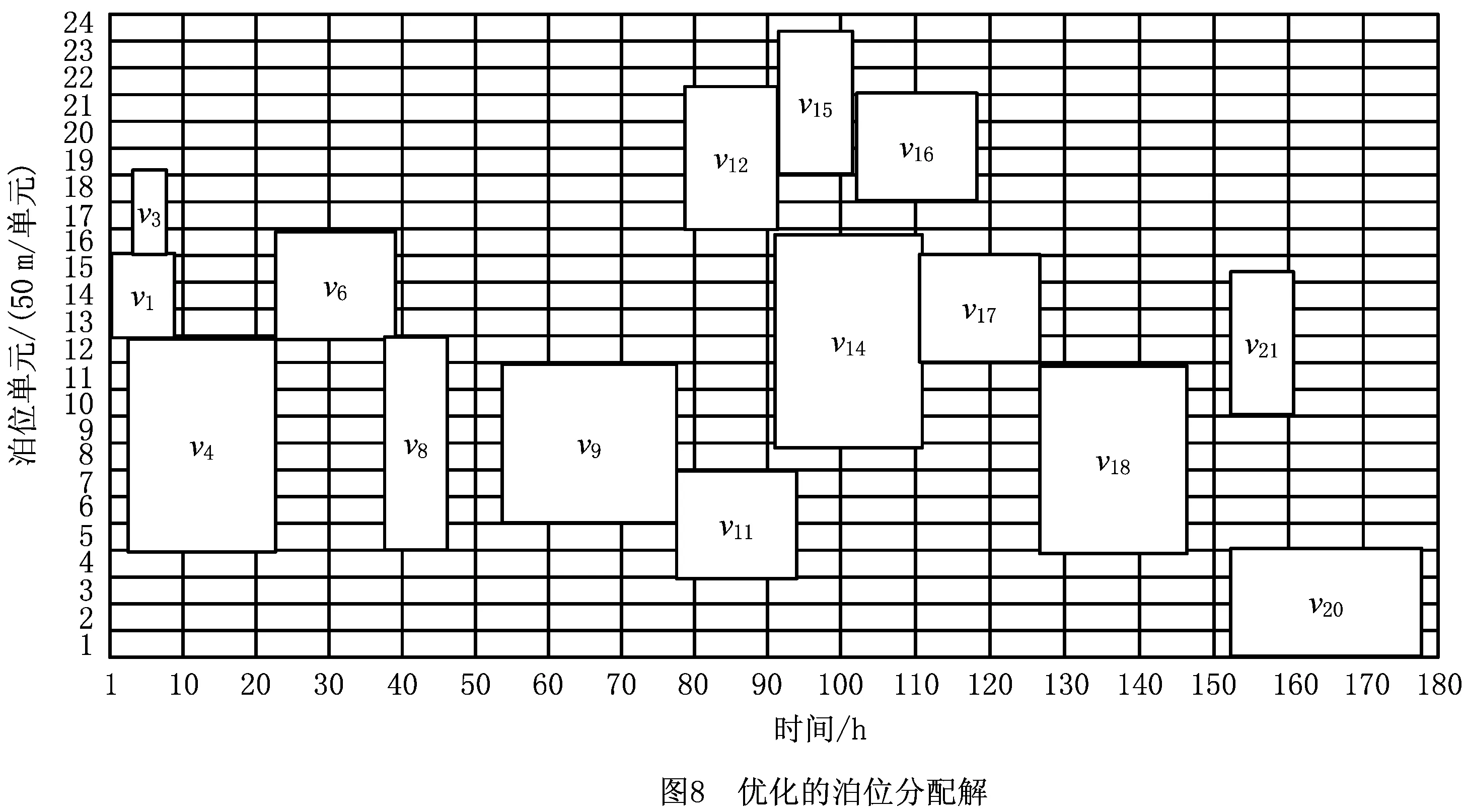
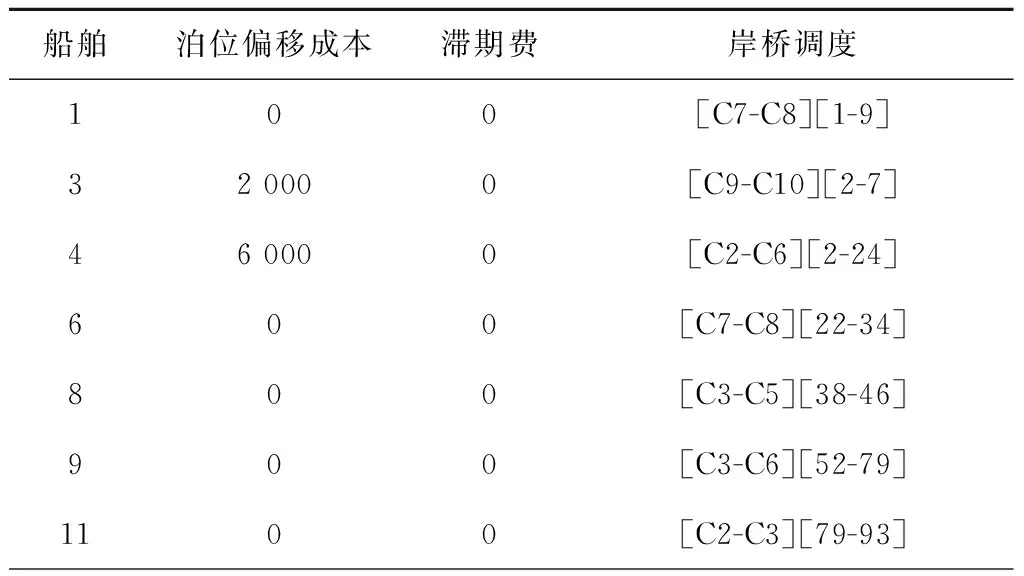
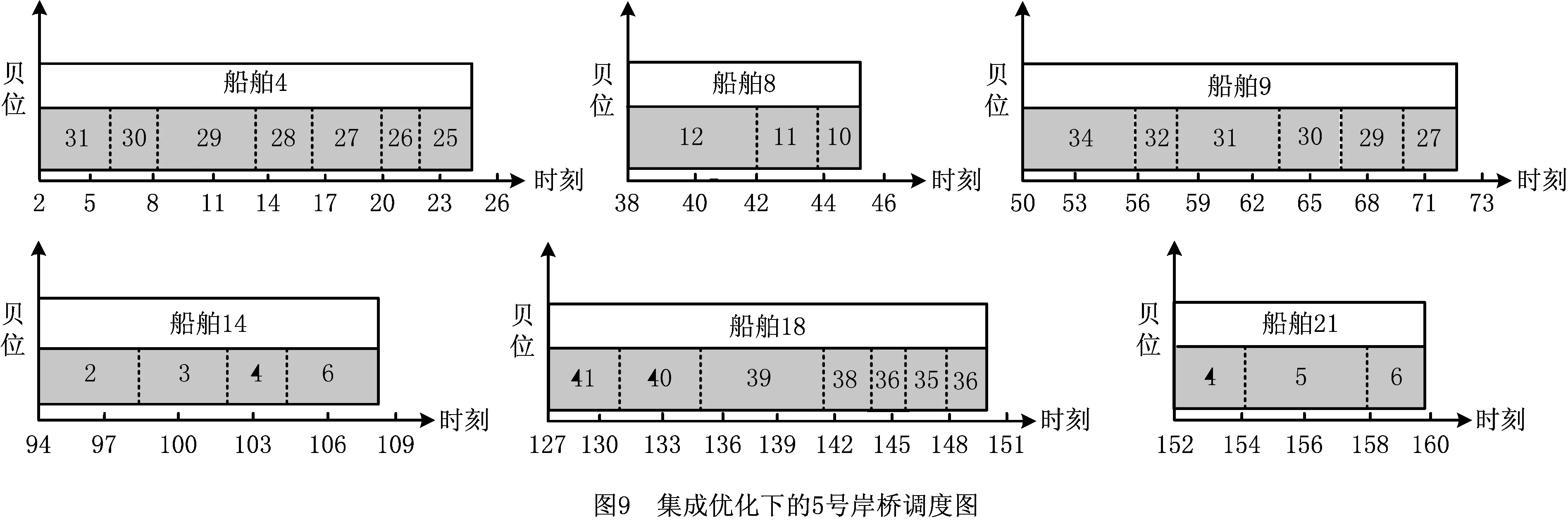
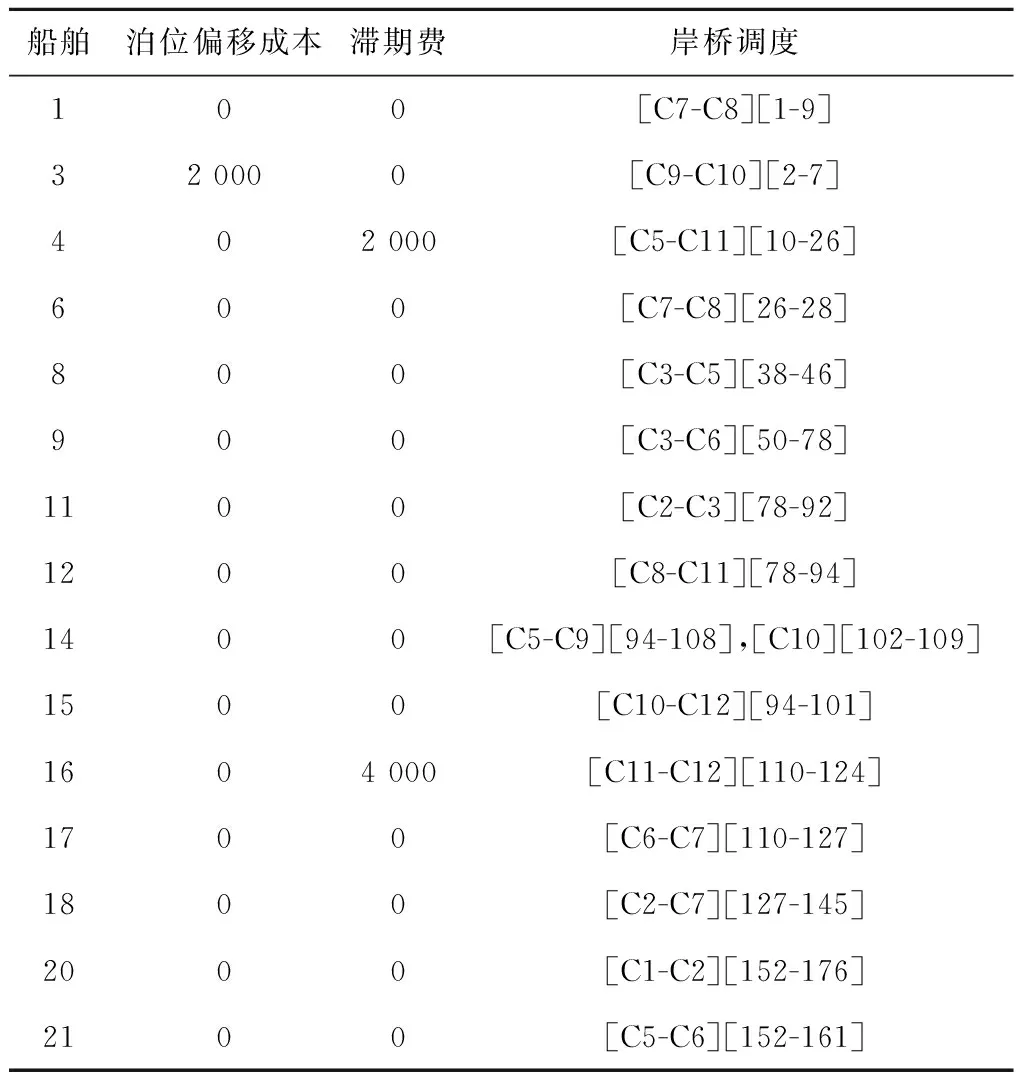
步骤4n=n+1。若n 步骤5按照先到先服务的原则生成剩余船舶列表Vr={Vr1,Vr2,…,Vrm},列表大小为m。令i=1。 步骤6令船舶Vri的到港时间为ei,靠泊时间为ti,装卸时间为hi,离泊时间为si。令n=1。 步骤7若船舶Vri与船舶Vri-n有重叠靠泊位置,则ti=max(ti-n+hi,ei),否则ti=ei。 步骤8n=n+1。若n 上述靠泊时间的生成方法,每次生成时间时都会检查是否与之前已安排靠泊的船舶有空间上的重叠,若有,则推迟靠泊时间,从而避免了船舶靠泊时在空间和时间上的重叠。 (3)染色体合法性检验 除去(2)中处理的约束,针对主模型中的约束(2)~(4),采用惩罚的方式处理染色体违反约束的情况。令v1和v2分别为船舶靠泊位置违反约束和船舶服务总岸桥数违反约束的基因总数,则v1和v2的更新规则如下: 步骤1v1=0,v2=0。 步骤2船舶集合V={v1,v2,…,vn},集合大小为n。令i=1。 步骤3令船舶vi靠泊位置为bi,船长为li,泊位长度为L。若bi+li≥L,则v1=v1+1,否则v1=v1。 步骤4i=i+1。若i 步骤5时刻集合T={t1,t2,…,tn},集合大小为n。令i=1。 步骤6令时刻ti所有在泊船舶集合为V={v1,v2,…,vn},所分配的岸桥集合为R={r1,r2,…,rn}。 步骤9i=i+1。若i (4)适应度计算 在适应度函数中引入罚函数来处理违反约束的染色体,其中:c为正整数,d1和d2为惩罚因子,v1和v2分别为船舶靠泊位置违反约束和船舶服务岸桥总数违反约束的基因总数,f1为主模型目标函数中去除θ的部分,f2为子模型1的目标函数。适应度函数如下: 阶段一的适应度函数为 F1(f1)=max(f1+d1·v1+d2·v2)- (f1+d1·v1+d2·v2)+c; 阶段二的适应度函数为 F2(f1,f2)=max(f1+f2+d1·v1+d2·v2)- (f1+f2+d1·v1+d2·v2)+c。 (5)交叉与变异操作 染色体的交叉策略为单切点交叉,随机选择父染色体的一个切点位置,分别对第一层与第二层进行单切点交叉;染色体的变异策略为随机选择个体的某一位基因,将其更改为满足变动范围条件下的随机值,以保证染色体的合法性。 (6)阶段转换操作 阶段一结束后,对得到的进化种群进行如下处理:检查种群中是否有相同基因的染色体,若有,则将其中任意一条去除,依据初始种群中染色体的产生方式重新产生染色体。检查完毕后,将该种群作为阶段二的初始种群,开始第二阶段的运算。 (7)终止条件 设阶段一和阶段二的迭代次数分别为N1和N2,达到相应的迭代次数后,分别终止阶段一和阶段二。 群组分割算法的主要思想为:以前后两台无空闲岸桥的时刻构成一个独立的阶段,在该阶段的每一时刻,以空闲的岸桥为分割点,将其余的作业岸桥分割为若干岸桥组进行调度,具体内容如下:根据主模型得到的解,可以获得每个时刻在泊位上作业船舶所分配的岸桥数,如图3所示。该图表示在T时刻,船舶1有2台岸桥为其服务,船舶2与船舶3均有3台岸桥为其服务。 因此,将t∈T中所有无空闲岸桥的tf提取出来组成集合Tf,该集合中的相邻元素组成子调度阶段的起始状态与终止状态,每个子调度阶段可并行求解。子调度阶段如图6所示。 在子调度阶段中,某时刻只需确定空闲岸桥的位置,即能确定该时刻的问题的解,子模型1所描述的问题即转化为求解每个子调度阶段所闲置的岸桥,采用动态规划法进行求解,具体求解步骤如下: (1)阶段划分 将调度子阶段的每个时间段划分为一个阶段,船舶的靠泊和离泊触发为时间段的分界线。 (2)状态变量xk描述k阶段处于空闲的岸桥集合。 (3)决策变量uk下一阶段空闲的岸桥。 (4)状态转移方程xk+1=uk。 (6)基本方程 式中:k=1,2,…,n 针对群组分割的特点,对决策变量uk制定如下规则: 本算例采用文献[1]中的数据进行求解。泊位长度为1 200 m,分为24个单元;时间为200 h,分为200个单元;岸桥数为12;岸桥作业干扰系数设为0.95;单位泊位偏移成本为1 000 元,单位时间滞期成本为2 000 元,岸桥移动成本为5 元/m;船舶的任务贝位与贝位的作业量通过正态分布的随机数产生。 实验运行在2.6 GHz Intel Core i5-3230 M CPU和4 GB内存的计算机上,采用MATLAB R2016a编码,线性规划求解部分调用CPLEX规划求解器进行求解。遗传算法参数如下:种群规模为100,第一阶段迭代次数为200,第二阶段迭代次数为600,交叉率为0.5,变异率为0.05;惩罚系数d1=4 000,d2=2 000。因原始数据中没有装卸贝位的集装箱装载量数据,该数据通过正态分布的随机数产生。 当V=15时,某次实验的遗传算法第二阶段的平均适应度随迭代次数的变化图像如图7所示。可以看出,种群从480代左右逐渐开始收敛。泊位分配解如图8所示,其中船舶4、船舶9、船舶14与船舶18为大型船舶。可以看出,为了使得大型船舶在涨潮时刻进入泊位,船舶4与船舶14通过泊位偏移达到按时进泊的目的,而船舶9和船舶18则分别通过等待2 h和5 h的方式达到乘潮作业的目的。因为算例中均为卸船船舶,所以无需考虑船舶出港时的潮汐影响。岸桥调度结果如表1所示,以5号岸桥为例,其对应的任务贝位如图9所示。 表1 岸桥调度解 船舶泊位偏移成本滞期费岸桥调度100[C7-C8][1-9]32 0000[C9-C10][2-7]46 0000[C2-C6][2-24]600[C7-C8][22-34]800[C3-C5][38-46]900[C3-C6][52-79]1100[C2-C3][79-93] 续表1 为了检验算法的效果,建立数学模型求解本问题的下界,并将其与本文算法进行比较。 在忽略潮汐时间窗与岸桥跨越约束的前提下,建立泊位分配与岸桥分配模型如下: (1)参数 (2)决策变量 (3)目标函数 (32) s.t. li+bi≤L,∀i∈V; (33) ∀t∈T; (34) (35) M(1-yij)+bj≥bi+li+1,∀i,j∈V; (36) M(1-zij)+SBj≥EBi+1,∀i,j∈V; (37) yij+yji+zij+zji≥1,∀i,j∈V; (38) (39) ∀i∈V,∀t∈T; (40) (41) (42) (43) (44) (45) (46) (47) (48) (49) (50) ∀i,j∈V,∀k∈K; (51) ∀i∈V,∀k∈K。 (52) 使用CPLEX与本文算法求解不同船舶规模的问题,运算结果如表2所示。 表2 算法对比 此外,基于算例中的泊位数据,采用随机生成到港船舶数据的方式,仿真实验在不同时间单元与不同船舶规模下的算法运算时间,以及在相同时间单元下不同船舶规模与不同岸桥数量下的算法运算时间。表3所示为岸桥数为12时,不同船舶规模与时间单元下的算法CPU时间。表4为时间单元为40时,不同船舶规模与岸桥数量下的算法CPU时间。 表3 不同船舶规模和时间单元下的算法CPU时间 s 表4 不同船舶规模和岸桥数量下的算法CPU时间 s 基于表3和表4的数据,算法运算时间的变化趋势如图10和图11所示。由图10可以看出,在岸桥数量固定的前提下,当船舶规模一定时,算法运算时间随时间单元的增加而增长;当时间单元一定时,算法运算时间随船舶规模的增大而增长。其中,当船舶规模在45以下时,运算时间增长幅度较小,而当船舶规模为50与55时,算法运算时间呈大幅度增长,但运算时间均在25 min之内。由图11可以看出,在时间单元固定的前提下,当岸桥数量一定时,算法运算时间随船舶规模的增大而增长;当船舶规模一定时,岸桥数量的增长对算法运算时间的影响不大。综上,本文算法在求解问题的时间单元为80 h以内时,运算时间不随船舶规模和岸桥数量的增加而显著增加,当船舶数量在45艘以下时少于9 min。 本文研究的是泊位分配、岸桥分配与岸桥调度的集成优化问题,需要通过与单独优化的方案进行比较来验证方案的有效性。单独优化的步骤为:以泊位偏移成本最小与滞期成本最小为目标确定泊位分配与岸桥数量分配方案,然后以岸桥移动成本最小为目标确定岸桥调度方案,得到单独优化后的调度方案。 泊位分配如图12所示,岸桥调度结果表5所示。 单独优化方案下的泊位偏移成本与滞期成本之和为8 000 元,岸桥移动成本为51 500 元,所花费的所有成本为59 500 元;集成方案的岸桥移动的泊位偏移成本与滞期成本之和为11 000 元,岸桥移动成本为42 000 元,总成本为53 000 元。由此可以看出,单独优化下的方案虽然在泊位偏移成本与滞期成本之和上小于集成优化方案,但其成本的节约建立在最大限度地调用岸桥资源的基础上,因此在岸桥移动成本上远大于集成优化方案,其总成本也超过集成优化方案,集成方案所节约的成本为10.92%。此外,因单独优化方案未考虑潮汐影响,船舶4、船舶9、船舶14与船舶18的靠泊时间均不为涨潮时刻,因此在实际作业中无法按计划正常靠泊。 表5 岸桥调度解 船舶泊位偏移成本滞期费岸桥调度100[C7-C8][1-9]32 0000[C9-C10][2-7]402 000[C5-C11][10-26]600[C7-C8][26-28]800[C3-C5][38-46]900[C3-C6][50-78]1100[C2-C3][78-92]1200[C8-C11][78-94]1400[C5-C9][94-108],[C10][102-109]1500[C10-C12][94-101]1604 000[C11-C12][110-124]1700[C6-C7][110-127]1800[C2-C7][127-145]2000[C1-C2][152-176]2100[C5-C6][152-161] 本文在考虑潮汐影响的前提下,研究了岸桥与连续泊位集成调度问题,以泊位偏移成本、岸桥移动成本与滞期成本之和最少为目标,建立了泊位分配—岸桥分配主模型、岸桥调度子模型,并设计了三阶段混合遗传算法进行求解。文中重在集成连续泊位分配、岸桥分配和岸桥调度,兼顾大船乘潮进出港的现实约束。算例实验结果表明,采用本文模型和算法得出的集成调度方案优于单独优化的方案。本文算法的求解时间并不随问题规模的增大而显著增加,适用于集装箱港口昼夜作业的实际调度。 未来将增加不同船型需要不同潮高进出港和集卡数量限制等现实约束,研究连续泊位、岸桥和集卡的集成调度问题。

2.3 群组分割算法
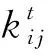
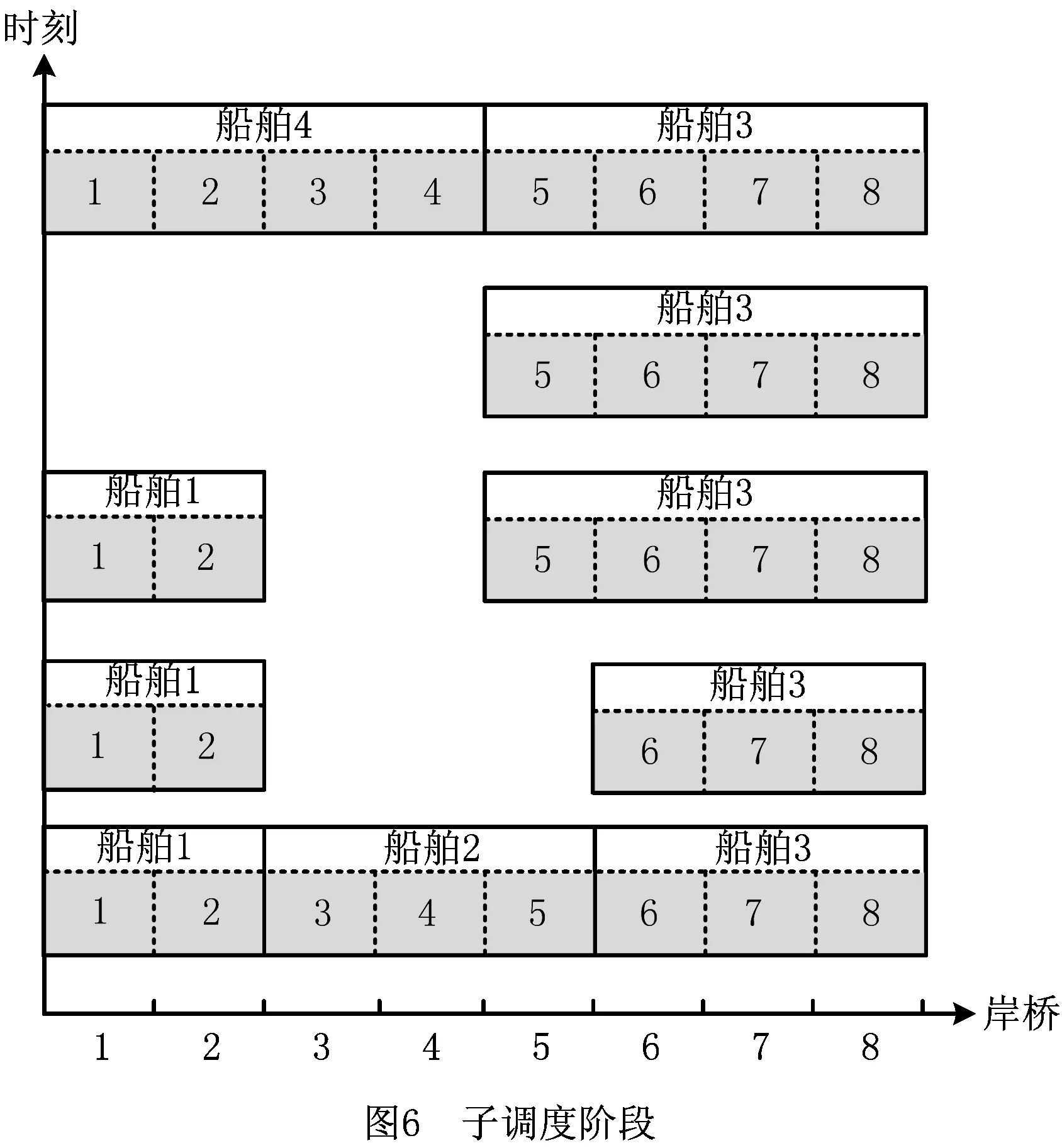
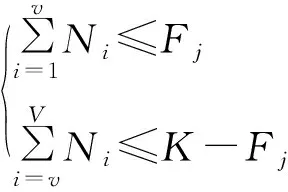
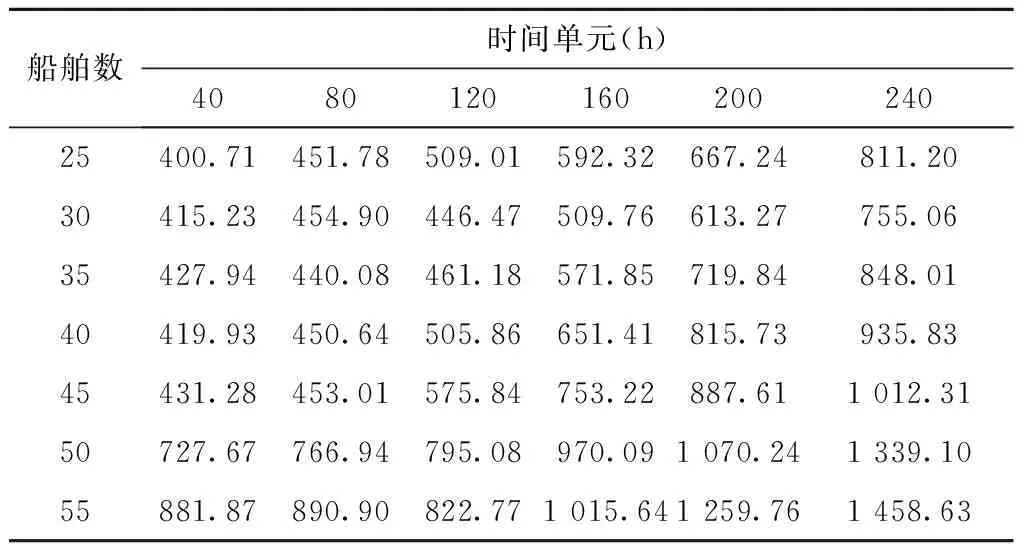
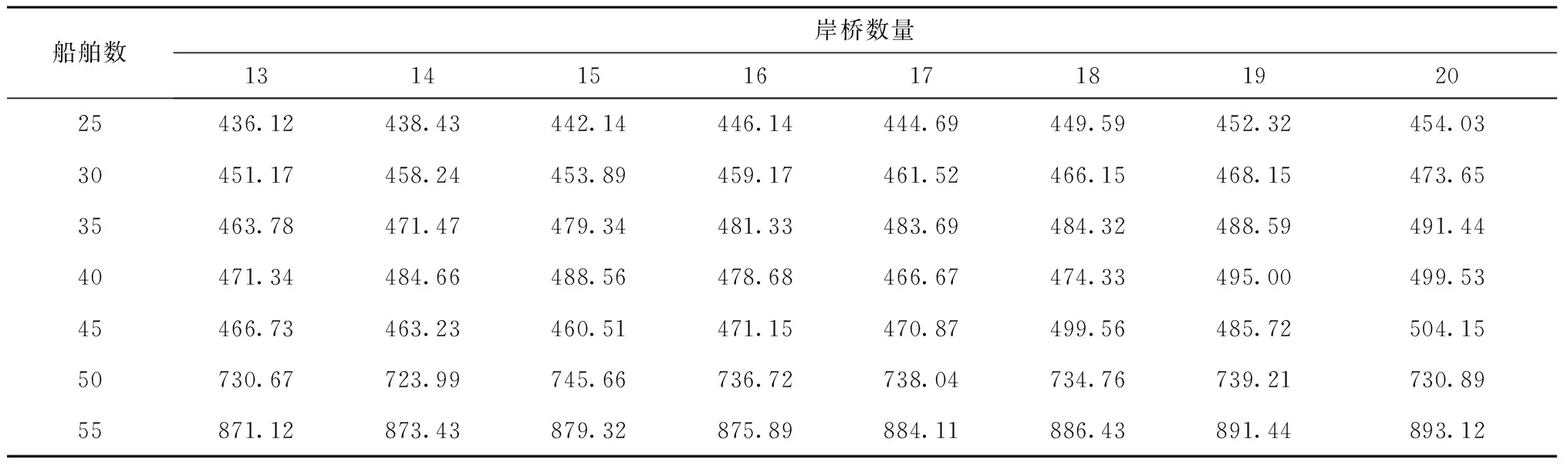
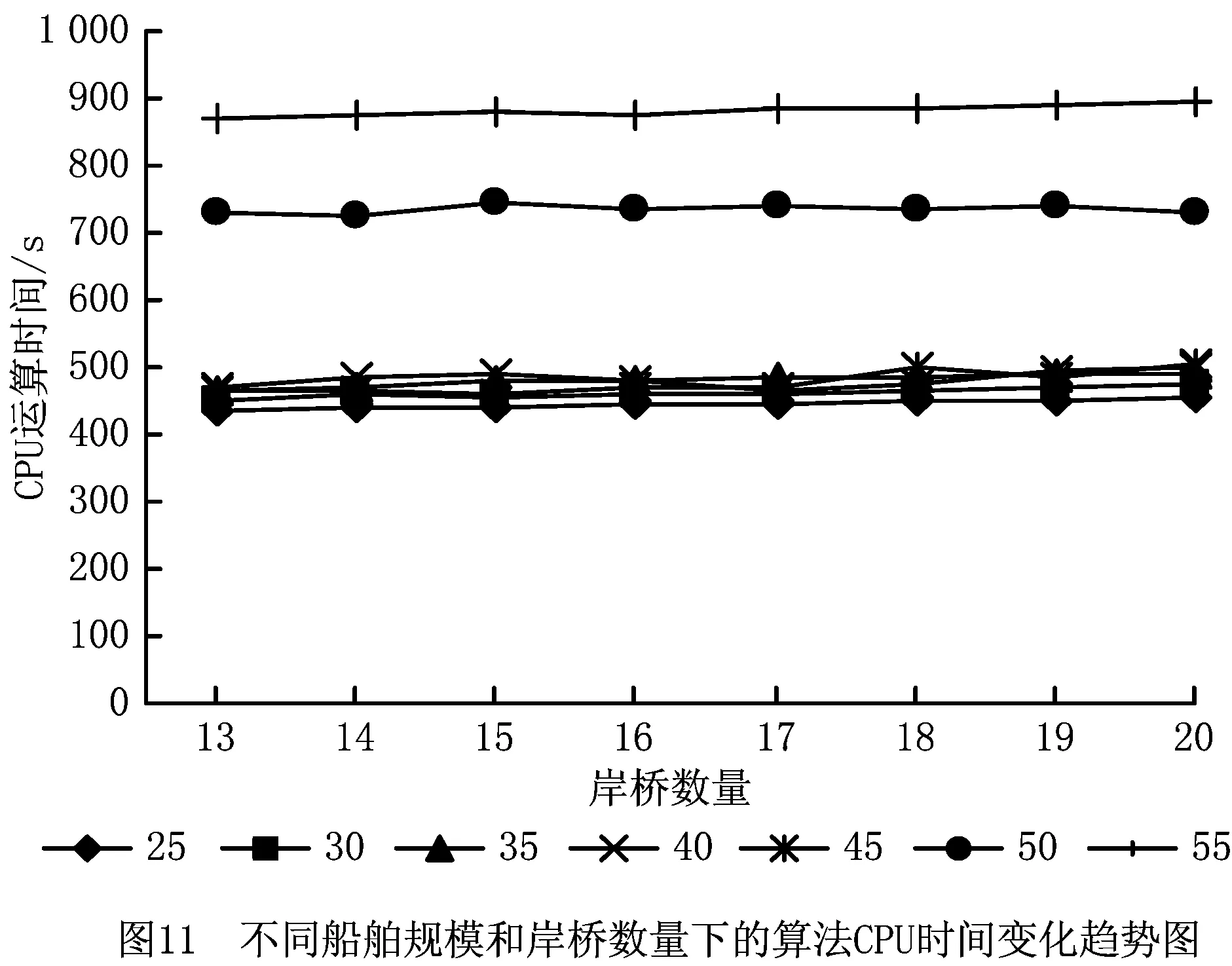
3 算例
3.1 算例求解

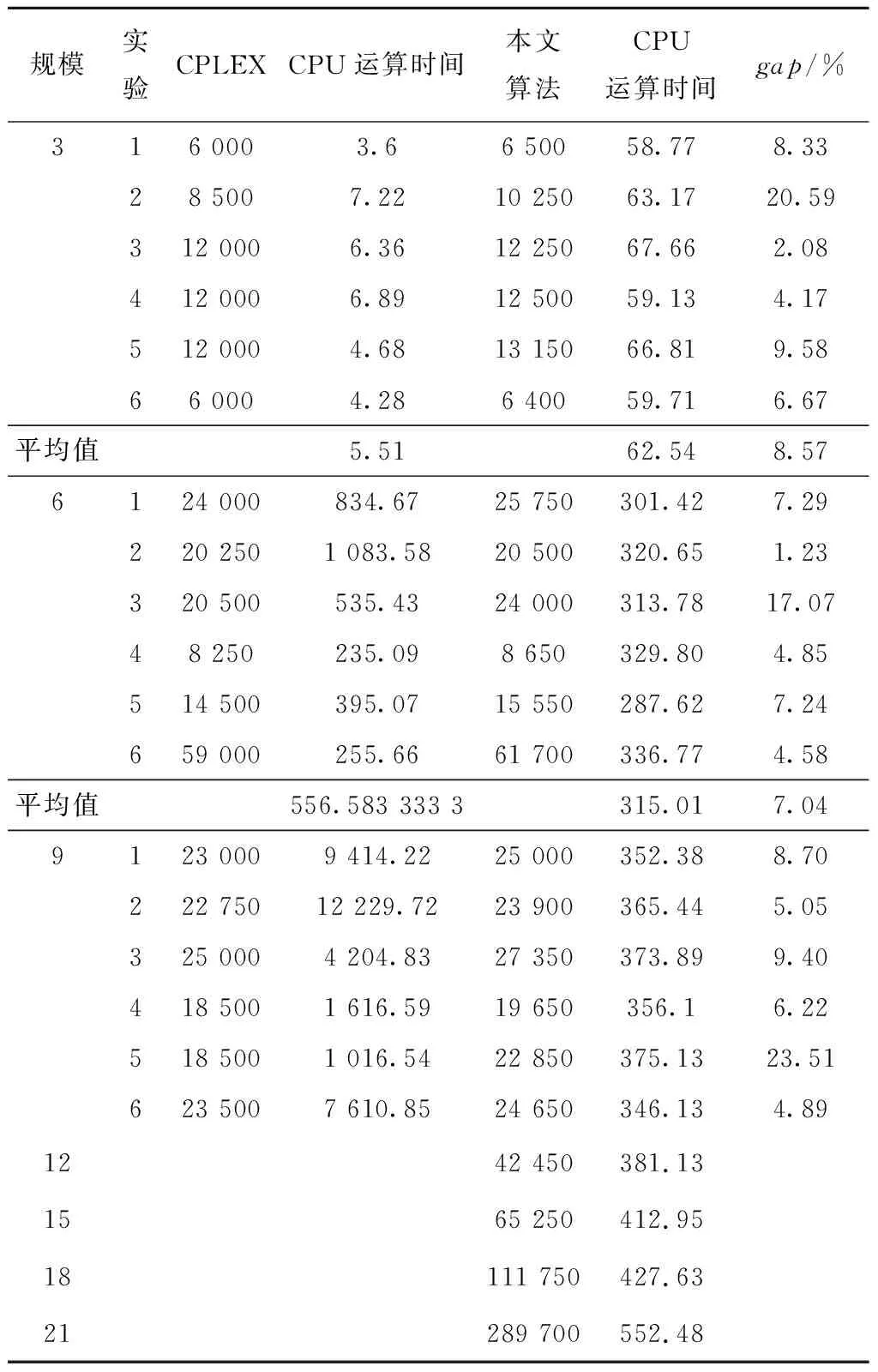
3.2 算法对比
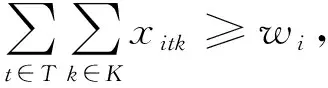
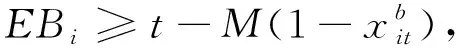
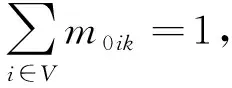
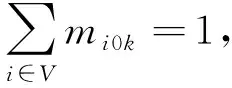
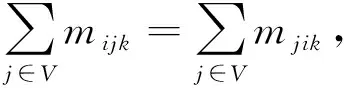
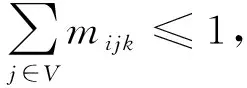
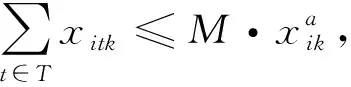
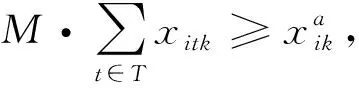
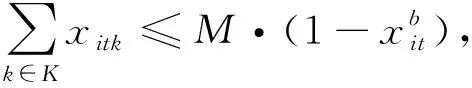

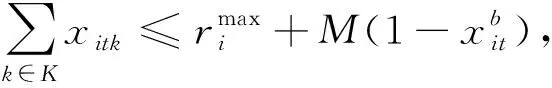

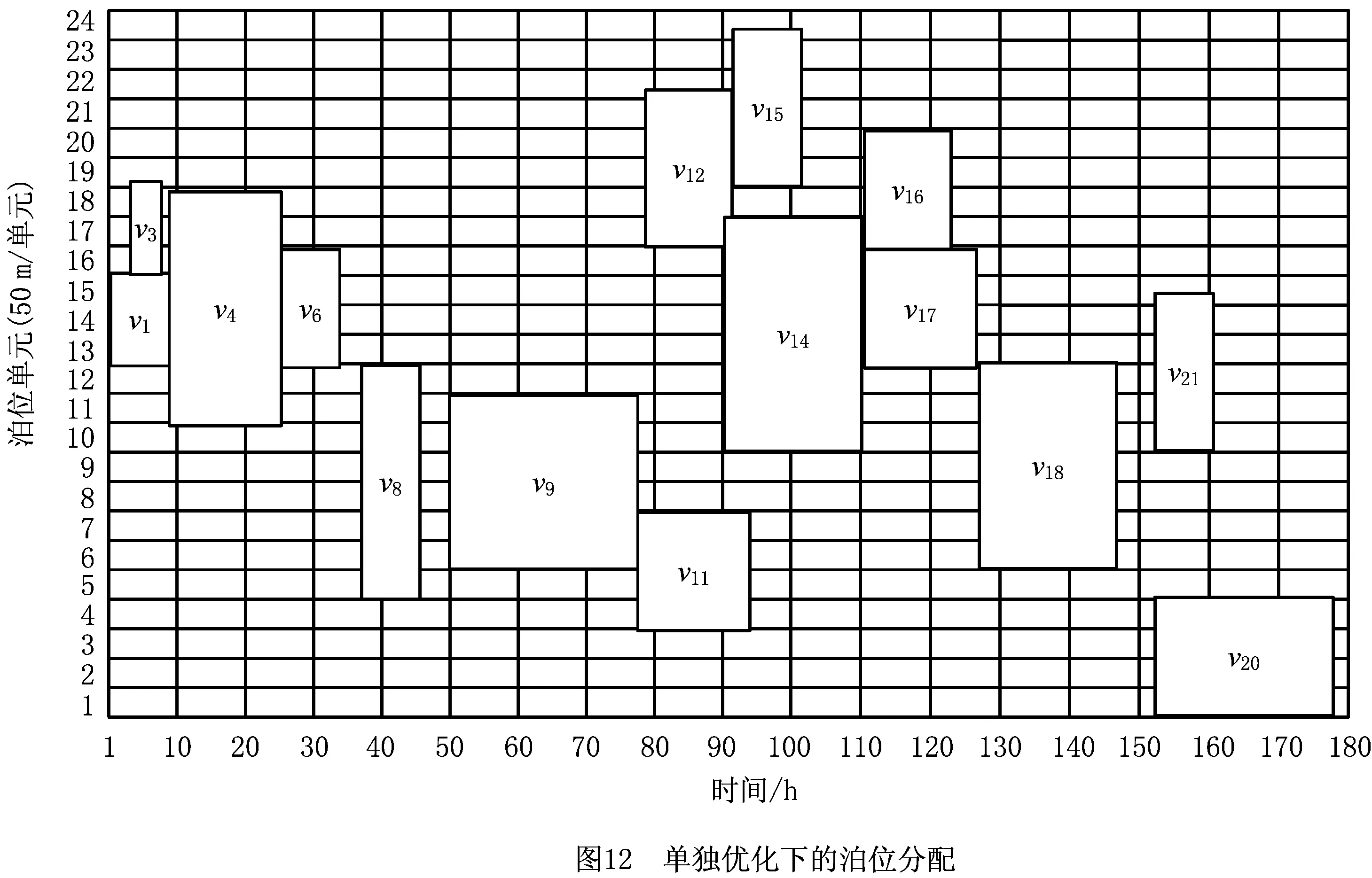
3.3 方案有效性验证
4 结束语

