基于显著性检测与特征匹配的目标识别方法*

孙世宇，张 岩，杜玉龙，李建增，李德良，范 聪

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

随着计算机技术的日益发展，如何模仿视觉系统迅速定位图像内感兴趣目标区域，实现目标的精确识别，已成为计算机视觉领域的热点问题。本文拟采用目标显著性检测算法与特征匹配算子相结合的策略进行目标识别，来缩小计算区域，同时避免误识别，改善目标识别的精度与速度。

在显著性检测方面：Itti等人[1]最早提出显著性检测问题，通过颜色、亮度和方向等特征，实现高对比度显著区域的检测。Hou等人[2]基于谱残差在频谱域内去除冗余信息，在空域得到显著信息。Guo等人[3]基于四元相位谱，通过提取相位谱实现检测。Liu 等人[4]从 3 种特征来描述图像，并在 CRF[5]框架下融合特征来实现检测。Shen等人[6]将图像信息分为低秩结构和稀疏噪声，认为低秩矩阵代表图像中的背景区域，稀疏矩阵为显著区域，基于底层和高层特征，利用低秩稀疏分解技术实现检测。Yang等人[7]结合联合条件随机场与区分字典学习方法，计算最小化能量函数实现显著性检测。Zhang等人[8]通过计算区域之间的方向和距离的相似性，利用区域聚类进行显著性检测。Chen等人[9]引入CNN模型，检测效果良好。Wen等人[10]利用深度玻尔兹曼特征学习算法对显著性区域进行判断，提高检测精度。

在特征匹配方面：Lowe提出并完善了尺度不变特征匹配算法（Scale Invariant Feature Transform，SIFT）[11]。Bay等人提出了快速鲁棒性特征算法（Speeded Up Robust Features，SURF）[12]。该算法在尺度空间内使用快速海森矩阵检测得到候选点，然后利用小波扇形环绕法定向，同时利用小波响应生成64维描述向量。虽然该算法的实时性与鲁棒性较SIFT大幅增强，但快速海森矩阵鲁棒性较弱，所以该算法的鲁棒性仍待加强。Leutenegger提出了二进制鲁棒性尺度不变的特征算法（Binary Robust Invariant Scalable Keypoints，BRISK）[13]。该算法在近似尺度空间中利用基于加速段检验的自适应通用角点检测子（Adaptive and Generic corner detection based on the Accelerated Segment Test，AGAST）[14]计算特征分数，同时利用长距离迭代法定向，使运行效率大幅提升，但尺度空间构建没有进行滤波，所以该算法的鲁棒性不强。Alahi等人提出一种快速视网膜特征描述子（Fast Retina Keypoint，FREAK）[15]。该描述子速度完全满足实时需求，但鲁棒性较弱。Pablo等人提出一种风式特征算法（KAZE）[16]。该算法构造了稳定的非线性尺度空间，利用用海森矩阵检测，同时考虑了区域交叠带，使其对于各种变换比SURF、BRISK等更加稳健，但非线性尺度空间运算复杂，运行效率大幅下降。Pablo等人对KAZE进行了改良，提出一种快速风式特征算法（Accelerated-KAZE）[17]。该算法利用快速显示扩散方程（Fast Explicit Diffusion，FED），动态改善了非线性尺度空间的构建，使得检测的运行效率与鲁棒性大幅增强，同时提出一种改进的局部差异二进制描述符（Modified-Local Difference Binary，M-LDB），使得描述子的速度大大提高，但描述子的鲁棒性弱于KAZE描述子。传统目标识别算法存在的问题有：

1）传统算法的鲁棒性较弱；当输入图像存在多个目标，或前景目标与背景相似度较高时，算法所检测到的区域边界不明确，检测结果中存在显著区域不完整等问题。

2）高斯滤波无法同时保持图像细节并消除噪声，检测子的计算速度仍待提高。所以欲改良传统显著性检测算法和特征匹配算法的鲁棒性与实时性问题，其重点是解决特征学习能力的加强、目标边界的确定、尺度空间的构建、检测算子的选用的问题。

1 目标识别流程概述

本文提出一种基于显著性检测与特征匹配的目标识别方法，方法流程如图1所示。

图1 本文算法示意图

2 改进的显著性检测方法

2.1 深度交叉卷积神经网络模型

基于视神经传递原理，对传统CNN型进行改进，设计了一种深度交叉卷积神经网络模型（Deep Cross Convolution Neural Network，DCCNN），算法结构如图2所示。

图2 DCCNN结构示意图

对于目标图像，首先利用两条数据变换流flow A和flow B同时进行特征提取。然后利用不同底层卷积变换步长提取局部特征，输送到全连接层。最后在DCCNN顶端对特征进行交叉混合，剔除重复和冗余信息，获得更加丰富的目标特征。

假设第L层权值矩阵为ωL，输出值为XL，前向输出值为YL，则前向输出函数fL为：

在第L层网络的损失函数为：

式中，ui为第i个样本，vi为第i个样本的标签值，N为样本总数，ω为权值，α为正则化系数，用于L2正则化抑制过拟合。

权值矩阵可通过下式进行更新：

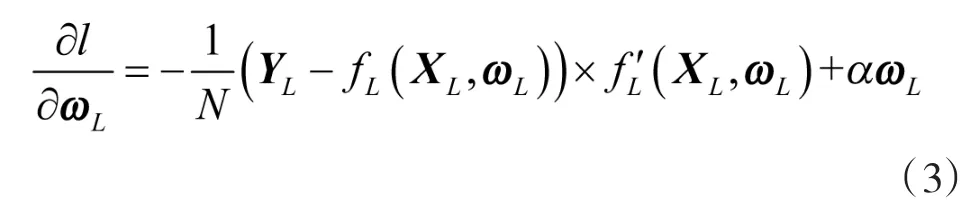
在全连接层混合交叉处，采用链式求导法对函数内的ωL进行更新：

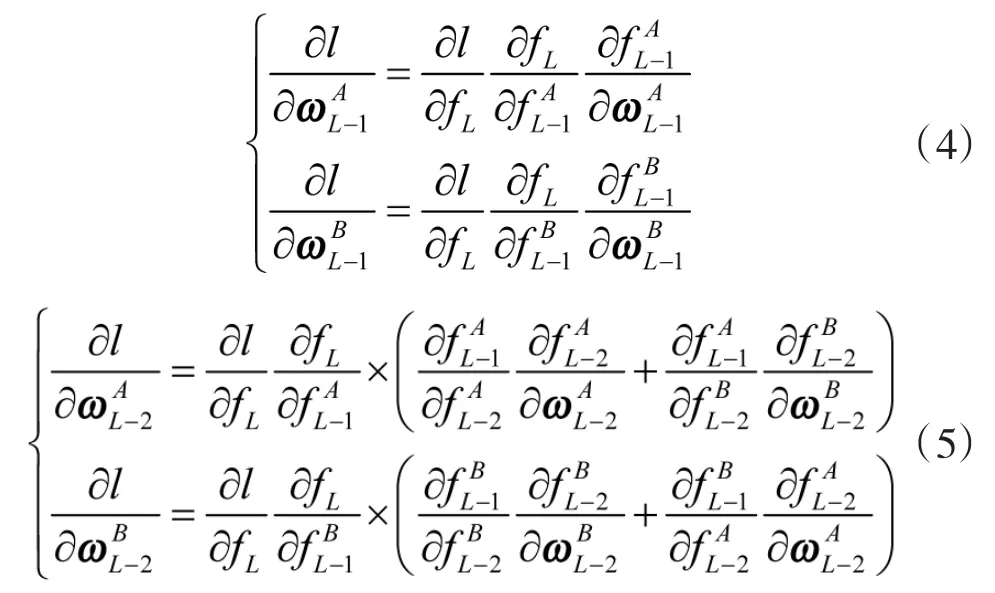
式中，ωA和fA分别表示flow A中的权值矩阵和前向输出函数；ωB和fB分别表示flow B中的权值矩阵和前向输出函数。神经网络的目标函数T为：

利用随机梯度下降法对T不断迭代得到最优解。

2.2 基于DCCNN的显著性粗糙检测

显著性区域实质上是图像中某种突出特征所在的区域，可以利用DCCNN模型实现粗糙检测，具体流程如图3所示。

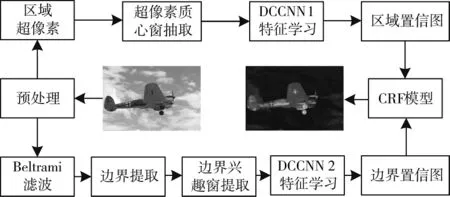
图3 显著性检测模型

首先分别利用Beltrami流滤波器和SLIC算法来提取边界与区域特征。然后通过两个并行的DCCNN模型对特征进行学习，得到边界置信图和区域置信图。最后在联合CRF框架下融合两种特征，从而实现显著性粗糙检测。

对于输入图像I（x，y）中的局部块Si（x，y），定义其对应的标记函数为si，则在联合CRF框架下的显著性检测条件概率分布模型p（si|Si）为：

式中，Z为归一化配分函数，E（·）为能量函数，标记函数为si，0代表不显著，1代表显著。

图像局部块的显著度值ai为：

则显著性区域A为：

将能量函数模型定义如下：

式中，α和φ均为定值，ωi代表权值系数，〈·〉代表局部块之间的平均对比度。

能量函数中加号前一项为数据能量项，其值由边界特征和区域特征共同决定，和分别为通过DCCNN学习得到的区域置信度和边界置信度。加号后一项为平滑能量项，该项代表不同局部块之间的连续性，用来判断显著性区域和非显著性区域之间的相似性。

标记函数si的集合是s通过最大后验概率maxp（si|Si）求取的。根据式（7），归一化配分函数Z并不依赖si，因此，在检测显著性区域时，可以将显著模型中maxp（si|Si）的求取问题转化为计算能量函数E（si，Si）最小值问题，即：

2.3 基于免交互GrabCut的显著性精确检测

在联合条件随机场内基于边界和区域特征的显著性检测结果较为粗糙，其中存在显著性目标不完整等问题。为了提高检测精度，本文在利用联合CRF模型获取粗糙检测结果的基础上，提出一种免交互Grabcut算法实现精确检测，算法框架如图4所示。

图4 显著性精确检测框架

首先对图像进行二值化处理，其中阈值由大津法选定。然后通过形态学腐蚀与膨胀运算，采用多边形窗代替矩形窗进行GrabCut分割。最后创建高斯混合模型来求取Gibbs能量函数最小值，利用最大流最小分割法实现显著性区域的精确检测，算法效果如图5所示。

图5 标记框选取示意图

免交互GrabCut算法得到的连通区域比实际尺寸更大，这避免了检测误差导致的显著目标缺失，保证了检测精度和目标完整性。

3 改进的特征检测子

3.1 非线性尺度空间建模

非线性扩散滤波方法如下式所示：

式中，L为输入图像，t为时间，div为散度运算符，为梯度运算符，Lσ为L经高斯核为σ的滤波结果，k为对比因子。

3.2 非线性尺度空间的快速求解

本文采用FED算法[17]求解非线性扩散方程，首先根据尺度参数求出进化时间，如下式所示：

式中，σi为尺度参数单位矩阵，ti为进化时间。

然后基于因式分解的盒子滤波求解不同步长，如下式所示：

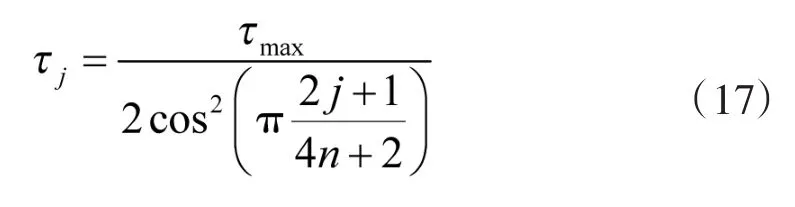
最后求解非线性偏微分方程如下式所示：

式中，I为单位矩阵，Al为传导运算符。

3.3 AGAST算子检测

选择合适的特征分数计算方法是在尺度空间中找到特征点的必要条件。在众多特征分数计算方法中，FAST的鲁棒性与速度优势是极为显著的。鉴于BRISK引入AGAST计算分数取得的成功，本实验引入AGAST计算特征分数，AGAST算子的本质是：如果在待检测点邻域内，灰度值小于（或大于）待检测点的点数大于阈值，则该检测点被判别为关键点。经Rosten测试，9个像素参与比较的模板检测性能较强，所以本文采用AGAST9-16（圆周上共有16个像素，需比较像素的个数为9）计算特征分数。

利用该算子计算尺度空间内的每一层的特征分数，然后进行非极大值抑制与亚像素级矫正得到候选点，再利用小波响应扇形环绕法[12]为候选点定向，得到特征点。

4 实验验证

笔记本计算机配置：处理器为2.5 GHz i7第4代，系统为64位Win10，编程环境为链接OpenCV 3.10的Visual Studio 2015（SIFT与SURF是从OpenCV 2.41中提取加载的）。

4.1 显著性检测实验

本实验采用MSRA10K和ECSSD数据库对传统显著性检测算法与本文显著性检测算法进行对比分析，两个数据库中分别含有10 000张和1 000张测试图像，包含人、动植物、交通工具和建筑等各种目标。

各算法部分显著性检测结果如下页图6与图7所示，其中最左侧为实验原图，最右侧为数据库提供的显著性真值GT，从左至右依次为LC、SR、AC、FT、SeR、CA、SEG、HC、SWD、FES、MC、GR、COV 以及本文显著性检测算法的实验结果。其中，本文显著性检测算法的检测结果与GT最为接近，显著图轮廓最清晰，算法性能最强。

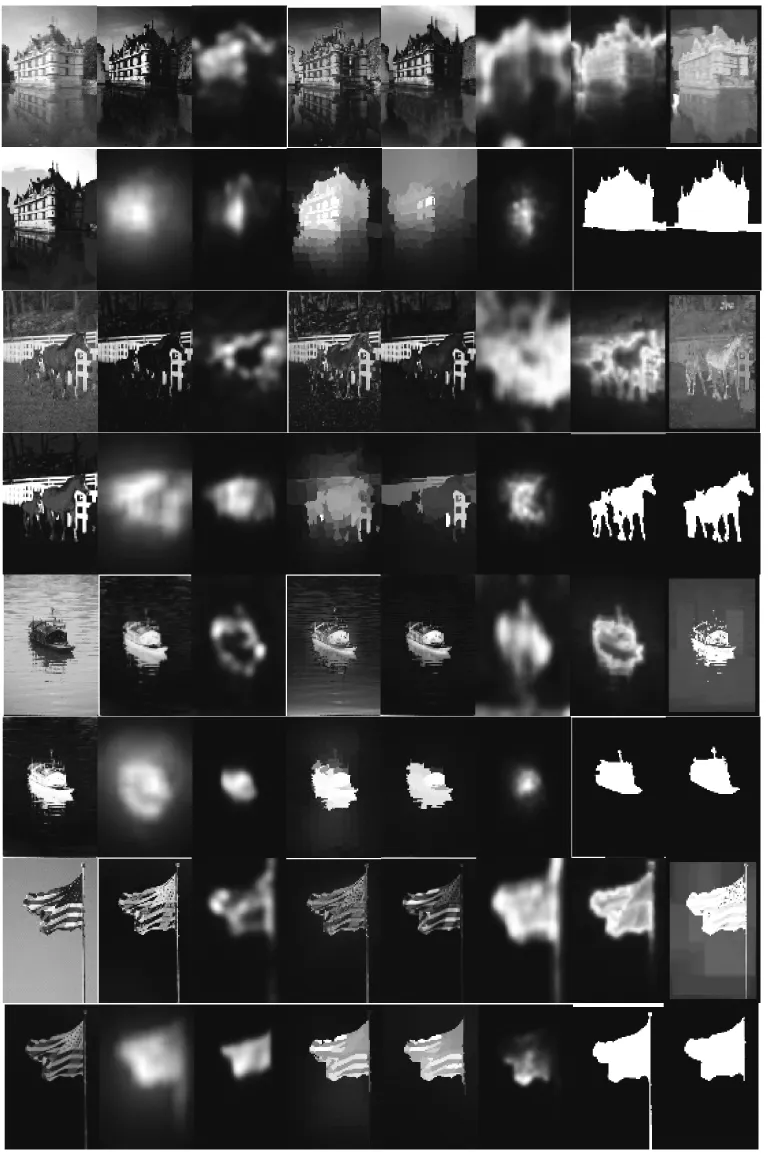
图6 MSRA10K数据库显著性检测结果

图7 ECSSD数据库显著性检测

为定量说明算法的性能，通过F值[18]、查全率R和查准率P评价算法性能，其计算公式分别为：

式中，SR代表总检测区域；GT代表显著性真值；β2代表权重。为避免扩大显著性检测区域造成的召回率过高问题，将权重 β2设置为 0.3[19]。

如图8所示，随着横坐标R值逐渐增大，各种显著性检测算法的P值均递减，本文显著性检测算法的P-R曲线更靠近右上方，性能更强。

图8 MSRA10K和ECSSD数据库实验结果

4.2 特征检测子实验

本实验采用标准测试图集[12]对比不同检测子的性能，如图9所示，从该数据集选取5个数据子集（含图像间的单应矩阵），通过测定复现率[20]来评判检测子性能。

图9 测试所用图片集

如下页图10所示，对改进的特征检测子的实验结果分析如下：

1）KAZE在非线性尺度空间内采用Hessian进行检测，该算法与Fast-Hessian的对比说明，非线性滤波器构建尺度空间对检测响应在视点、尺度与模糊变换的特征检测性能有大幅度提升。

2）AGAST与 Fast-Hessian的对比说明，AGAST在模糊、视点与JPEG压缩变换方面的鲁棒性均有较大提升，这是将AGAST引入本文特征检测子的重要原因。

图10 不同变换条件下的复现率比较

3）BRISK的广泛使用验证了利用AGAST计算尺度空间内特征分数的可行性。同时BRISK对于视点变换、JPEG压缩、尺度以及旋转变换的鲁棒性较弱，也验证了尺度空间构建引入滤波的重要性。

4）由于改进的特征检测子对于照度、模糊、视点与JPEG压缩变换的鲁棒性较强，可以说明快速非线性尺度空间构建与AGAST配合时性能比较优良。

综上所述，改进的特征检测子鲁棒性更强。

利用传统算法与改进的特征检测子，分别对Graf（800×640像素）图像序列中的第一张图像进行100次实验，取均值后进行对比分析。

如表1所示，将耗时结果分析如下：虽然构建非线性尺度空间增加了计算量，但引入FED算法加速了非线性尺度空间的构建，基于AGAST计算特征分数提高了检测速度，所以改进的特征检测子的执行速度大大领先于KAZE与SIFT。

4.3 目标识别实验

1）建立模板库。本实验选取3本具有相似性表面的书籍作为实验对象，对3个实验对象分别获取10个不同角度的影像（1 280×960像素）建立了模板库。该模板尺寸与待识别的图像尺寸相差约30%，均有照度、模糊与噪声影响，部分模板如图11所示。

表1 算法耗时比较

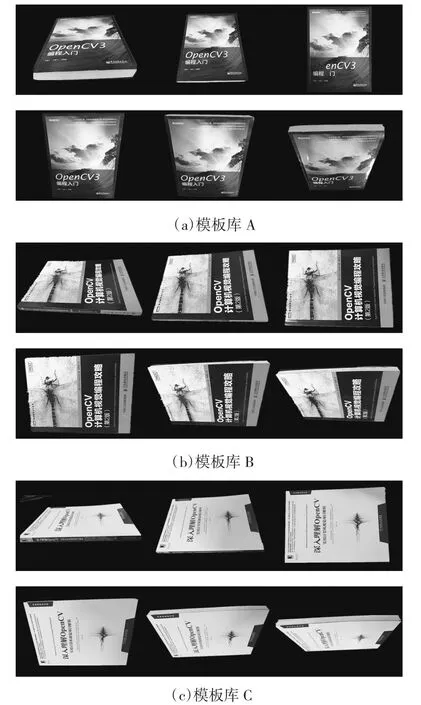
图11 目标模板库

2）目标评判标准。本实验以目标图像与模板库的平均匹配率作为评判标准，平均匹配率越高，则判定目标与模板库越相似。平均匹配率为待识别目标图像的已匹配特征点数与某个模板库中每个模板的总特征点数比值的平均值，定义式如下：

式中，H为平均匹配率，k为模板库中模板总数，Mi为待识别目标图像与第i个模板匹配的特征点数，Ni为第i个模板中的总特征点数。

3）实验结果分析

图12 识别效果

识别效果如图12所示，首先通过显著性检测提取目标的显著性区域，然后将3个模板库的所有模板并行与目标进行特征匹配，最后分别计算3个模板库的平均匹配率，从而实现目标的实时识别。

图12（d）为3个模板库的平均匹配率统计结果，其中模板库A的平均匹配率为81.66%，模板库B的平均匹配率为16.31%，模板库C的平均匹配率为1.62%，将检测到的目标判定为目标A。模板库B与C的平均匹配率较低，说明其模板与目标图像相同的特征较少，同理说明A中模板与目标图像相同的特征较多，验证了本算法的合理性与可行性。

5 结论

本文提出一种基于显著性检测与特征匹配的目标识别方法，并通过理论推导与实验验证说明了方法的可行性与优势，主要得到以下结论：1）交叉卷积神经网络模型内的交叉操作降低了目标信息的冗余度，提高了算法的学习能力。2）GrabCut算法的应用有效提高了目标区域的检测精度。3）改进的特征检测子的快速非线性尺度空间的鲁棒性与实时性比KAZE的非线性尺度空间更强。4）基于AGAST计算特征分数与基于海森矩阵计算特征分数相比，除照度变换外，对于其他变换的鲁棒性均有加强，且实时性更强。5）基于显著性检测与特征匹配的目标识别方法的鲁棒性与实时性较强。