DC/DC变换器的预测函数控制

吴津庆，葛芦生，陈宗祥，丁烨

(安徽工业大学电气与信息工程学院，安徽 马鞍山 243032)

DC/DC变换器应用广泛。如何运用先进的控制技术提高其稳态性能和动态调节性能，越来越受到学者们的关注[1-5]。模型预测控制(model predictive control, MPC)作为一种先进控制技术，目前已应用到DC/DC变换器的控制中[3-5]。预测函数控制(predictive functional control, PFC)是第三代模型预测控制算法，它将控制输入结构化，不仅克服了模型预测控制存在的控制输入不规律的问题，而且有效减少了在线计算量，提高了响应速度。文献[6]采用PFC-PID串级控制策略来控制主汽温控系统，提高了系统的鲁棒性。这种方法简单，而且具有实际应用价值。文献[7]将预测函数控制应用于并联机器人控制，并与计算转矩控制(computed torque control, CTC)和PID算法进行了对比，发现预测函数控制具有更好的跟踪性能和抗干扰性。

由于预测函数控制具有实时计算量小、鲁棒性强的特点，因此适用于快速控制系统[8]。鉴于此，本文设计了基于预测函数控制的Buck变换器，采用状态空间平均法建立预测模型，并进行反馈校正调节，通过优化二次型性能指标推导出占空比的表达式。最后通过仿真验证了该Buck变换器具有良好的稳态精度和较快的动态响应。

1 预测函数控制基本原理

1.1 控制变量

预测函数控制不仅具有模型预测控制的三大特征：预测模型、滚动优化、反馈校正，还有其独特的优点。PFC算法把每个时刻的控制输入看成是一系列已知基函数的线性组合：

(1)

式中：u(k+i)为(k+i)时刻的控制输入；P为预测优化时域长度；N为基函数的个数，N≤P；gkj(i)为基函数在t=iTS时刻的值，其中TS为采样周期；μj(k)为基函数的线性组合系数。由于基函数是已知的，对控制输入量的计算就转化成了对线性组合系数的计算。基函数可以根据被控对象的特性和设定值进行选择，通常选择阶跃函数、斜坡函数、指数函数等。

1.2 预测模型

PFC算法的预测模型采用线性离散状态空间描述方程的形式：

(2)

式中：Xm是预测模型的状态变量；ym为预测模型的输出；u为系统的控制输入；A、B、C是相应维数的矩阵或者向量。

1.3 参考轨迹

在实际控制过程中，为了让系统的输出值平滑地达到设定值，从而避免大幅度超调或者振荡现象，可以规定一条渐趋于设定值的曲线，即参考轨迹。参考轨迹可以选择多种形式，对于渐近稳定系统，通常采用一阶指数的形式：

yr(k+i)=c(k+i)-βi(c(k)-y(k))

i=1,2,…,P

(3)

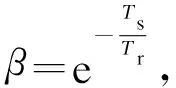
1.4 性能指标

预测函数控制的优化是对有限区域进行优化，通过时间的推移滚动式地进行下去。通常为使优化点上的预测值与参考轨迹值差值的平方和最小，优化的性能指标选取为

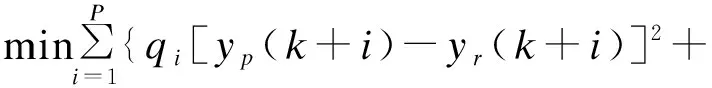
ri[u(k+i-1)]2}

(4)

式中：qi为差值的权重系数；ri为控制输入的权重系数；yp是校正后的模型预测输出值。

yp(k+i)=ym(k+i)+hie(k)i=1,2,…,P

(5)

式中，hi为误差系数，当模型存在误差时，可以调节hi使输出达到设定值；e为预测误差，可取为

e(k)=y(k)-ym(k)

(6)

为使式(4)能够取得最小值，令

(7)

式中，μ(k)=[μ1(k),μ2(k),…,μN(k)]T。对式(7)求解，可以得到基函数的线性组合系数，从而推导出控制输入的表达式。

2 Buck变换器的PFC控制器设计

2.1 Buck变换器数学模型

Buck变换器采用同步整流的方式，其拓扑结构如图1所示。

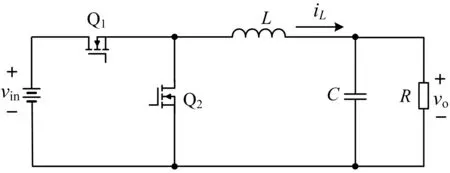
图1 同步整流Buck变换器拓扑结构

图1中，Q1为主开关管；Q2为同步整流管；L为电感；C为输出电容；R为负载电阻；vin和vo分别表示输入电压和输出电压。当Q1导通、Q2关断时，由KCL和KVL得到电路方程：

(8)

式中，kTs≤t≤(k+d(k))Ts。

当Q1关断、Q2导通时，电路方程为

(9)

式中，(k+d(k))Ts≤t≤(k+1)Ts。

运用状态空间平均法，将式(8)、(9)联立得

(10)

式中，kTs≤t≤(k+1)Ts。

选取电感电流iL(t)和输出电压vo(t)构成系统的状态向量，即x(t)=[iL(t)vo(t)]T，用欧拉前向差分离散的方法对式(10)离散化，得

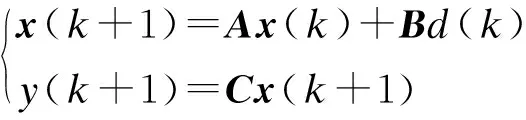
(11)

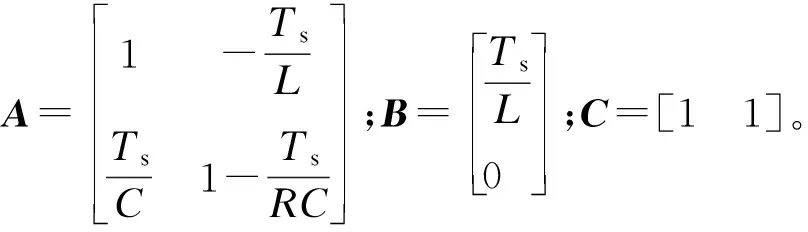
2.2 PFC控制器设计

施加PFC的Buck变换器原理图如图2所示，整个系统可以看成是单输入单输出系统，输入变量即为控制输入d(k)，输出变量为输出电压vo。对Buck变换器进行控制是为了得到一个稳定的输出电压，这相当于设定值固定不变，在此选择阶跃函数作为基函数[9]，则控制变量为

d(k+i)=μii=0,1,…,P-1

(12)

递推得到(k+i)时刻的模型预测值：

(13)

由式(3)—(6)可以推导出

J(k)=‖D(k)-Gk·μ1‖2Q+‖H·μ1‖2R

(14)

式中：

D(k)=[D(k+1),D(k+2),…,D(k+P)]T，

D(k+i)=(1-βi)c(k)+βiy(k)-CAix(k)-hie(k)；

Q=diag (q1,q2,…,qp)；

R=diag (r1,r2,…,rp)；

H(p×1)=[1,1,…,1]T。

由式(7)可得

μ1=MD(k)

(15)

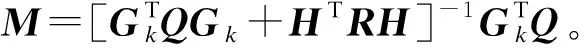
由于PFC采用滚动优化的控制策略，因此实际作用于被控对象的是控制序列的第一个控制量。控制输入可改写为

d(k)=k0c(k)+k1y(k)-K2x(k)-k3e(k)

(16)

式中：

k0=M[1-β，1-β2，…，1-βp]T；

k1=M[β,β2,…,βp]T；

K2=M[CA,CA2,…,CAp]T；

k3=M[h1,h2,…,hp]T。

可见，对于一个可用离散状态空间方程表示的系统，当c(k)、P、β、hi参数已知时，k0、k1、K2、k3都是已知量，可通过离线计算得出，y(k)、x(k)可通过对电路进行实时采样得到，因此PFC算法具有在线计算量小、易于实现的特点。

3 仿真验证

为了验证PFC算法对Buck变换器控制的有效性，在MATLAB/Simulink仿真环境下搭建了仿真模型。为了更好地模拟实际情况，在仿真模型中加入了电感和电容的寄生电阻参数。Buck变换器具体电路参数如表1所示。

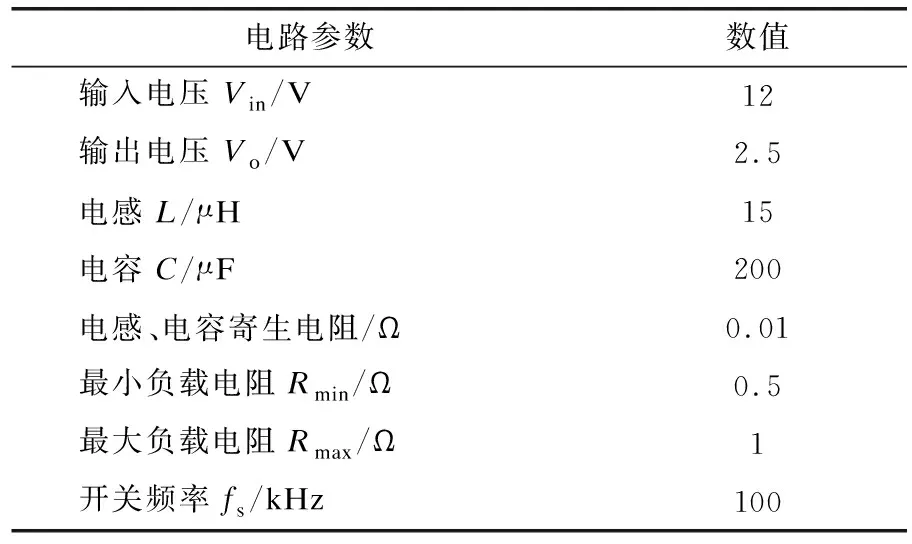
表1 Buck变换器电路参数

仿真中，对电感电流和输出电压进行采样，输入到PFC控制器，由式(16)计算出占空比d(k)，然后与峰值为1的三角波进行比较，产生PWM控制信号，控制开关管Q1和Q2导通和关断。PFC控制器的控制参数分别为：c(k)=2.5；Tr=1.5×10-5s；p=4；Q=diag(1,1,1,1)；R=0.01 diag (1,1,1,1)；h=[5 4.5 3.5 2.9]T。仿真波形如图3所示。

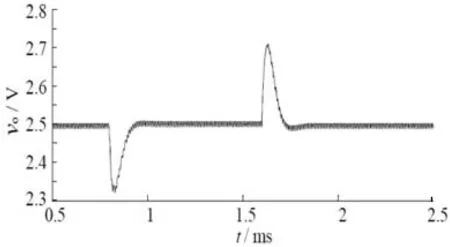
(a)输出电压vo波形

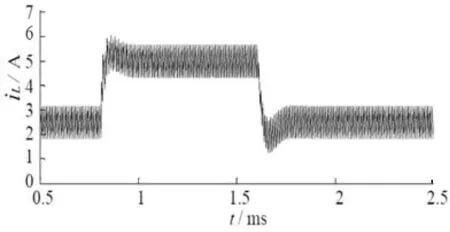
(b)输出电流iL波形

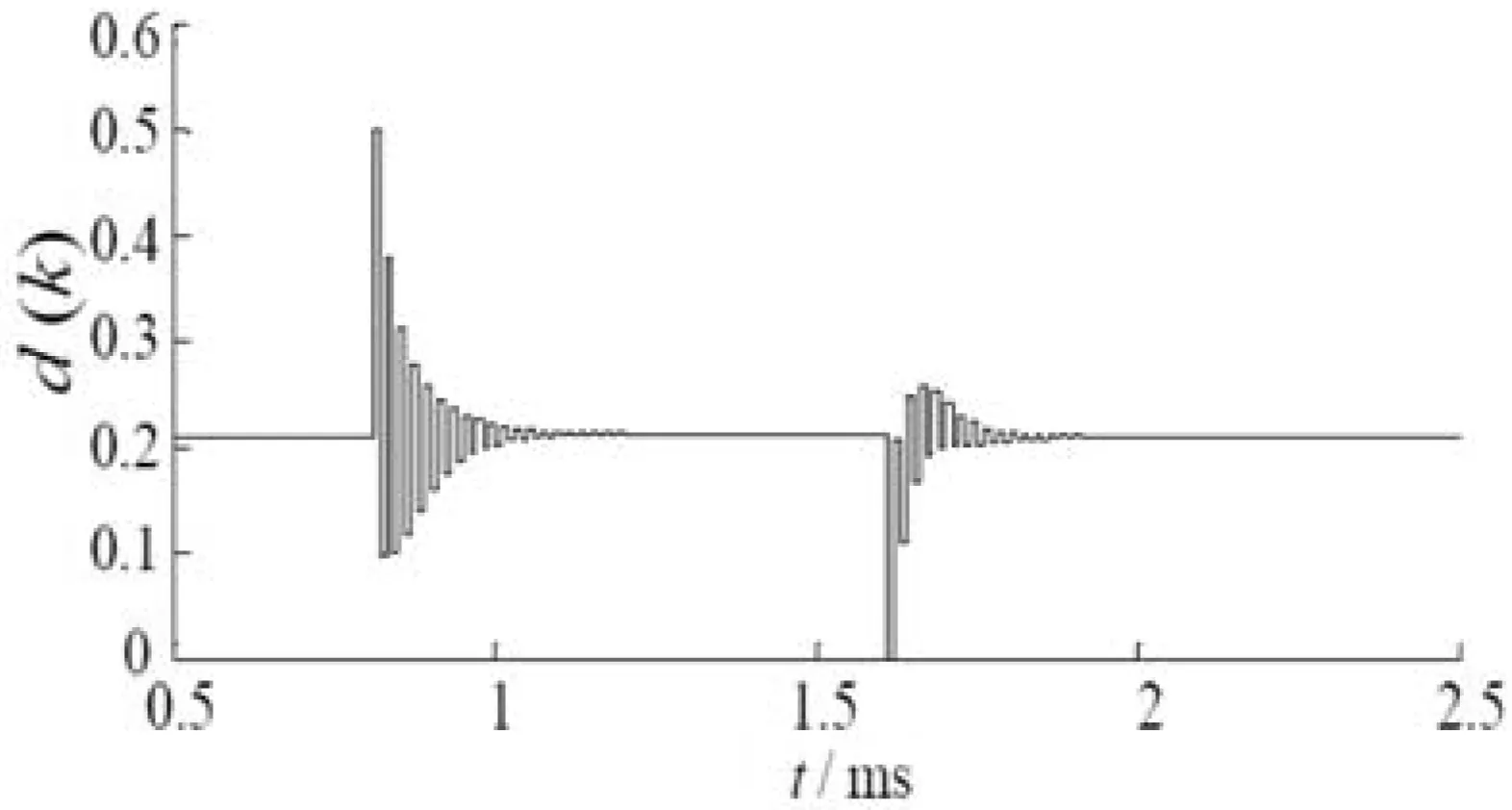
(c)占空比d(k)波形

在t=0.8 ms之前，Buck变换器的负载是1 Ω，输出电压稳定在给定值2.5 V，电感电流的平均值为2.5 A；在t=0.8 ms时，变换器的负载电阻从1 Ω切换到0.5 Ω，负载突然加大，输出电压有轻微下跌，下跌量约为0.18 V，接下去在PFC控制器作用下，输出电压快速跟踪到给定值2.5 V(经过12个开关周期)；在t=1.6 ms时，负载电阻又从0.5 Ω切换到1 Ω，负载减小，输出电压产生0.2 V左右的超调量，经过12个开关周期调节后恢复到2.5 V。在跳变负载时，占空比变化很大，这有助于快速调节输出电压到给定值；而在稳态时，占空比几乎没有波动，从而使得输出电压非常稳定，不会产生波动。

4 结论

本文介绍了预测函数控制的基本原理，结合状态空间方程计算控制输入，通过对Buck变换器进行状态平均法建模得到预测模型，进而推导出占空比的表达式。通过仿真，验证了本文设计的预测函数控制器能使Buck变换器具有良好的稳态性能和快速动态调节能力。