基于烟花算法的无线传感器网络节点定位

朱晓丽，高鹏

(1.万博科技职业学院计算机科学与技术系,安徽 合肥 230031； 2.安徽工业经济职业技术学院计算机与艺术学院,安徽 合肥 230051)

0 引言

无线传感器网络(wireless sensor networks, WSN)通常是自组织网络，它由大量低功耗的传感器节点组成，这些传感器节点分布在一些需要监测的区域，监控物理参数或环境状况，并将收集到的信息转移到汇聚节点。目前WSN已被应用于许多领域，如军事、工业、医学，用作目标跟踪、环境监测、事件检测等。一般自组织网络的路由问题主要是WSN定位问题。传感器节点往往随机分布，应用WSN的地方几乎都需要知道传感器的位置，因为采集的数据不含位置信息就没有实用价值。如果每个传感器节点都使用全球定位系统(global positioning system, GPS)获取节点位置信息，成本昂贵，通常不可行。一种解决方法是选择部分传感器作为锚节点，由GPS或手动配置获得锚节点定位信息，再结合不同技术估算其他传感器节点位置。

目前估算传感器节点位置的算法分为测距定位算法和无测距定位算法。无测距定位算法估计传感器的位置，利用的是相邻节点之间的连通性和拓扑信息[1]。测距定位算法估计传感器的位置，依赖于节点之间的距离，通过估算无线电信号接收强度(received signal strength, RSS)、到达时间(time of arrival, TOA)、到达时间差(time difference of arrival, TDOA)、到达角(angle-of-arrival, AOA)等获取节点之间的距离信息[2]。

WSN定位优化问题十分复杂，但是随机算法的产生及应用正逐渐解决这一问题。其中应用最广泛的是群智能算法，这是一种模拟生物群体集体智慧的算法。群智能算法在解决局部最优解和离散组合指数等复杂的优化问题上较为成功，但其在处理大规模优化问题上算法执行效率很低。为此，Tan和Zhu[3]在2010年提出了一种新的群智能算法——烟花算法(FWA)。本文将FWA应用于WSN节点定位，测量结果显示，和常见的几种算法相比，FWA定位误差较小，这为FWA在WSN节点定位上的应用提供了依据。

1 WSN节点定位的数学建模

在解决WSN定位问题上，测距定位算法准确性高,应用广泛,其中基于RSS的定位算法具有很强的测试和分析性能，因此本文选择RSS获取节点之间距离信息。

接收机越靠近发射机，接收信号的强度就越大。基于发送功率和接收功率之间的关系，可以估算两个节点之间的距离。由于不同节点使用的硬件不同或测量过程中环境噪声发生变化，测距误差会很大。此外，无线电反射引起的多径传播，会导致衰落现象，也会产生较大误差。为了减少这些误差，用对数正态阴影[4]描述无线信道衰落现象：

(1)

式中：Pt表示发射功率；PL(d0)表示路径损耗；d0和α分别是参考距离和路径损耗指数；Xσ在高斯分布N(0,σ2)中出现，表示无线电信号的噪声。测距技术只是定位算法的第一部分。第二部分是确定传感器节点的确切位置，使用锚节点的位置和通过RSS获得的不精确的距离计算所有传感器节点的位置。设锚节点坐标为(xj,yj)，若WSN包含N个未知传感器节点，(xi,yi)表示未知节点i(i=1,2,…,N)的坐标，则未知节点与锚节点之间的距离为

(2)

RSS定位算法测得的距离Rij和由式(2)得出距离dij之间的距离误差为

eij=(Rij-dij)2

(3)

假设节点i有M个相邻锚节点，定位误差公式变为

(4)

最终目的是最小化所有未知节点的误差总和，因此目标函数为

(5)

对目标函数进行优化是本文的研究重点，所选用的算法误差总和越小，WSN节点定位越准确。本文应用新型群智能算法——FWA对此问题进行优化。

2 烟花算法

将FWA这一迭代算法应用于WSN定位，通过迭代估算相邻节点的位置。测距定位算法在估算距离时使用单边或多边定位。这种方法可以减少所需的锚节点数量，降低硬件成本，但如果没有足够的锚节点，一些节点的位置是无法估算的。迭代多边算法还存在误差积累问题，且要求锚节点必须位于网络边缘[5-6]。

FWA在特定地点随机产生n个烟花。每个烟花xi产生的火花量为[7]

(6)

式中：参数m表示n个烟花产生的火花数量；ymax是最差烟花，ymax=max(f(xi))(i=1,2,…,n)；η代表用于避免除零错误分配的小常数。

制作的烟花爆炸振幅不同，建模如下：

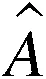
(7)

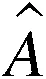
(8)

(9)

爆炸随机影响火花的尺寸z，定义为

z=round(d·x)

(10)

式中，d是维数优化数量，x代表随机数在0和1之间的均匀分布，所有选定的维度确定时，x也同时确定。文献[8—9]对此提出改进建议，将火花映射到新的位置公式：

ΔXk=Ai·rand(-1,1)

(11)

火花保持最佳位置x*并转移到下一处，根据其余的(N-1)个地点到其他地点的距离，选择它们的位置。某一位置xi和其他位置之间的距离由下式计算：

(12)

式中，K是烟花当前所有位置的集合[10]。基于公式(12)得到的距离，选择位置xi的概率为

(13)

文献[11]针对映射与变异算子提出了两项改进。映射操作符改为

(14)

高斯变异算子为

(15)

式中，XB是目前烟花爆炸发现火花的最好位置，且e=N(0,1)。

3 FWA在节点定位的应用

传感器节点被随机分布在需要监测的区域，其中一些被随机选择为锚节点。使用公式(1)建立无线信道模型，计算RSS以及节点之间的距离，用该烟花算法优化目标函数。本文对目标函数进行调整[12]，定义新的目标函数：

(16)

估计完未知传感器节点的位置后，更新锚节点位置，从而估计相邻传感器节点的位置。为了能够本地化，一个节点必须至少有3个相邻锚节点。在这种情况下，对于未知传感器节点，FWA使用公式(16)最小化目标函数。

在未知传感器节点有1个或2个相邻锚节点的情况下，采用FWA估计节点位置[13]。所有更新的锚节点从原始锚节点那里获取距离信息，如果未知传感器节点有1个或2个锚节点，则可以从相邻节点的位置数据发现它的位置，这极大地提高了节点定位精度。

4 实验结果

为了验证本文算法，利用MATLAB进行仿真实验，对比本文提出的FWA与回声定位算法、多点定位算法、DV-hop算法、粒子群优化算法、神经网络算法、改进的DV-hop算法的定位效果。对本文提出的FWA的实验参数进行设置：烟花数为5，迭代次数为5 000次，爆炸振幅为40，火花最小、最大数量分别设置为2和40。为了进行比较，调整初始实验条件，参数设置如下：

Pt=0 dBm,PL(d0)=55 dBm

当d0=1时，路径损耗指数α=4。监测区域设置为50 m×50 m，传输距离为25 m。每个实验开始时，传感器节点随机分布在该地区，锚节点随机选择。用公式(17)计算未知节点和锚节点之间的距离，其结果为实际距离，把实际距离与估计距离的比值作为定位误差，并考虑RSS的噪声干扰，同时结合已有参数值，得出噪声干扰因素下的距离值：

(17)

为了验证本文算法性能，分别测试各算法随RSS值、节点数、锚节点数和噪声标准偏差变化时的定位误差。图1为不同RSS值时定位误差的变化。可以看出，随着RSS值的增加，各个算法的定位误差逐渐减低，并趋于稳定，这是由于定位误差是根据所测试的估计距离的平均值得出。在此过程中，本文提出的FWA定位误差较小，定位精度较高。

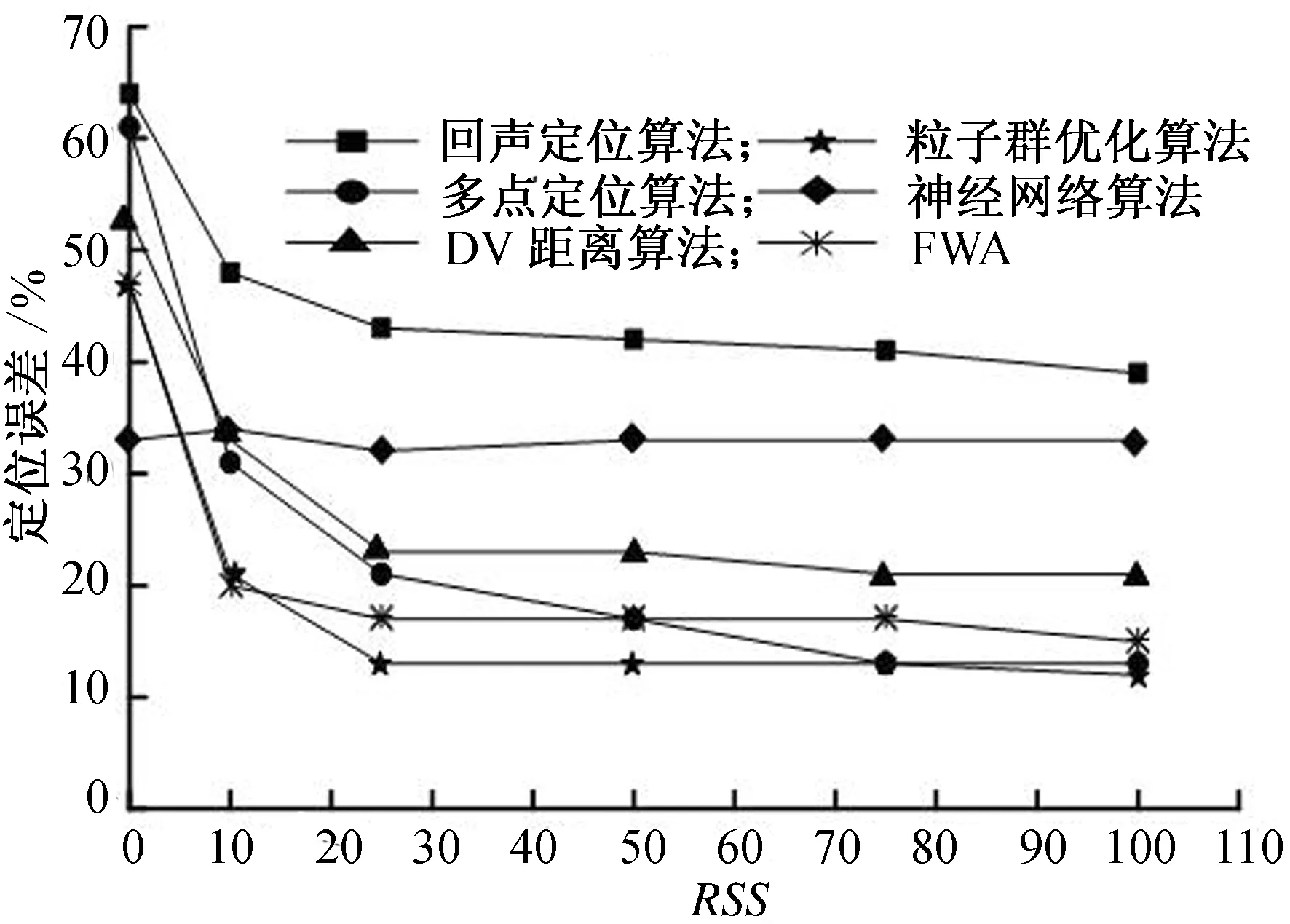
图1 RSS值与定位误差的关系

图2是节点数与定位误差之间的关系。可以看出，随着传感器节点数的增加，定位误差逐渐减小，同时定位误差趋于稳定。与其他算法相比，FWA的定位精度较高，且在节点数量变化过程中FWA定位误差值变化平稳，定位稳定性较好。

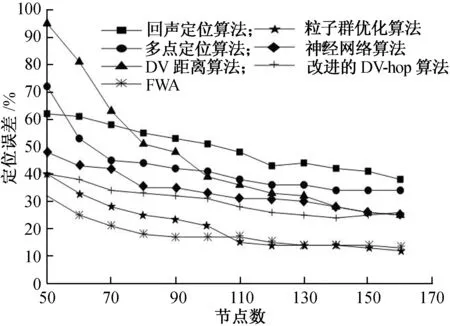
图2 节点数量与定位误差的关系

为了进一步验证本文算法的优越性，对不同锚节点数下的定位误差进行测试。由图3可知，选择更多的锚节点时定位误差较低。当62%以上的传感器节点被用作锚节点时，本文FWA定位误差最小，而锚节点比例小于50%时FWA相对于粒子群算法定位误差偏大。但总体来说，在锚节点数量一定时，FWA定位误差较小，定位较准确。

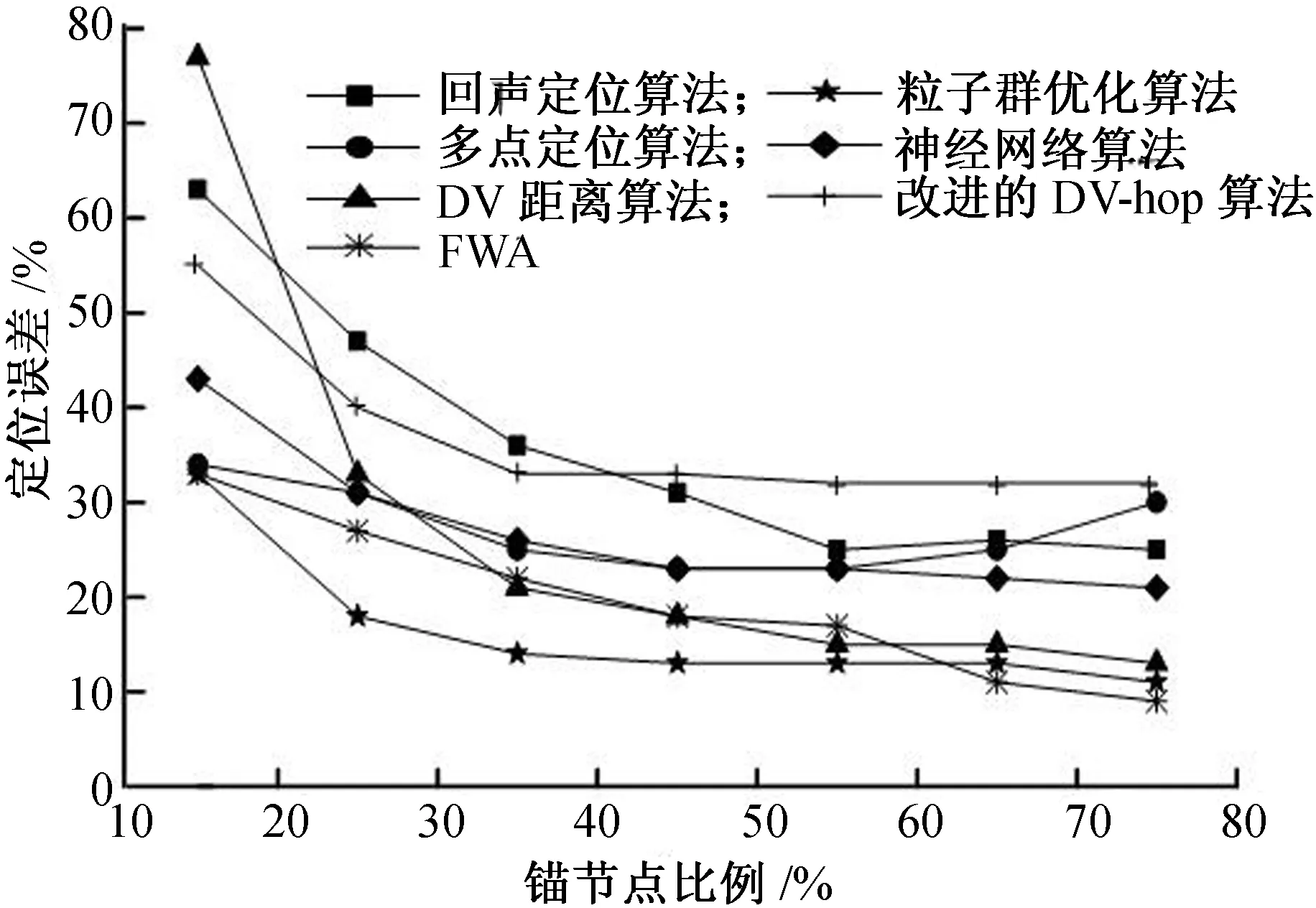
图3 锚节点数量与定位误差的关系

图4比较了6种不同算法的噪声水平和定位误差之间的关系。由此可知，随着噪声标准偏差的增大，定位误差变大，本文提出的FWA模型误差平稳增加，且误差最小，说明FWA在WSN节点定位时性能稳定、精度高。

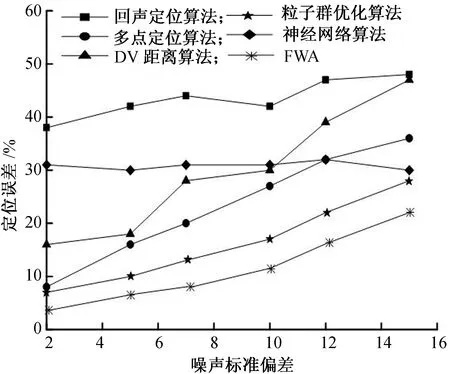
图4 噪声标准偏差与定位误差的关系

5 结语

为优化WSN节点定位精度，使节点定位误差更小，且整体性能更稳定，本文将一种新的群智能算法——FWA应用于WSN节点定位系统。通过更新传感器节点定位过程中的锚节点，使定位节点的数量增加。通过仿真实验，使用不同的实验参数，测试本文所提出的FWA在不同的网络规模、不同信号强度等情况下的应用效果。最后，将各实验因素综合起来，通过横向比较，证明了相比其他算法，FWA在进行无线网络节点定位时定位精度更高，性能更稳定。