基于DWT-FRFT变换和QR分解的盲数字水印算法

吴 强，彭亚雄

(贵州大学 大数据与信息工程学院，贵州 贵阳 550025)

数字水印是镶嵌在其他数据中具有可鉴别性的数字信号或模式，它的存在不影响宿主数据的可用性。因其具有安全性、不可感知性、可证明性以及稳健性等特点，数字水印作为一种有力的版权保护技术已得到广泛的应用。

对于数字水印算法，通常分为时域算法和频域算法。因频域算法抗攻击性更强，所以信息隐藏领域的研究更注重频域水印算法。研究人员针对基于离散余弦变换(Discrete Cosine Transform，DCT)的传统数字水印算法，提出了很多改进算法，这些算法对压缩和噪声攻击具有较好鲁棒性，但是无法有效抑制几何攻击。文献[1]提出一种基于量化的抗JPEG(Joint Photographic Experts Group)压缩攻击的鲁棒性水印算法。该算法对压缩攻击有很强的鲁棒性，但是抗几何攻击较弱；文献[2]提出了基于集成成像的DWT(Discrete Wavelet Transform)域水印技术。该技术稳健性较好，但抗攻击性较差；文献[3]提出了基于奇异值分解和Contourlet域的图像水印算法，进一步提高了水印的鲁棒性，但该算法耗时，复杂度较高。针对以上问题，本文提出了基于DWT-FRFT(Fractional Fourier Transform)变换和QR分解的盲数字水印算法，该算法将水印信息通过QIM(Quantized Index Modulation)重复嵌入到R的第1行，充分利用了R第1行的全部元素，安全性很高。QR分解相比奇异值分解，复杂度更低，在受到剪切、压缩、噪声、旋转攻击下，水印能很好地提取信息，鲁棒性较强。水印检测通过QIM及多数表决准则，未借用原始图像信息，属于盲水印算法。

1 相关技术

1.1 离散小波变换

离散小波变换(DWT)是时频域的一种转换，具有多尺度性的特点。其主要算法为MALLAT[4]算法：将数字图像系数A0进行小波分解，将A0通过低通滤波器(H)和高通滤波器(G)，然后采样得到低通系数(Aj+1)和高通系数(Dj+1)，具体公式如下

Aj+1(k)=∑nAj(n)H(n-2k)

(1)

Dj+1(k)=∑nAj(n)G(n-2k)

(2)

1.2 分数阶傅里叶变换

分数阶傅里叶变换(FRFT)具有时域和频域的双重特征以及旋转特性和角度连续性，因此被广泛使用于数字水印领域[5]。

二维图像信号f(s,t) 的p阶分数阶傅里叶变换为

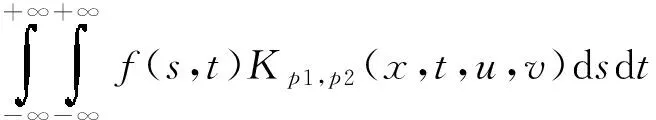
(3)

(4)

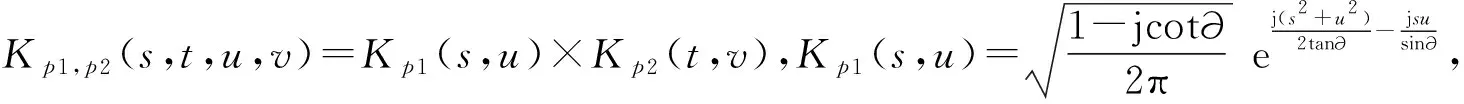
1.3 QR分解

QR分解是将矩阵分解为一个正交矩阵与上三角矩阵的乘积。在矩阵论中，m×n矩阵A可以表示为

A=QR

(5)

其中，R是上三角矩阵，Q是m×n的标准正交矩阵。当R第1行和其他行有相关性时，其第1行元素绝对值远远大于其他元素的绝对值。本文利用该性质，将水印信息嵌入R第1行，提高了水印图像的鲁棒性。该结论证明过程参见文献[6]。

1.4 量化索引调制技术

量化索引调制(QIM)技术是一种水印嵌入的经典算法，根据水印信息，把原始载体数据用量化器量化到不同的索引区间。水印检测时则根据调制后数据所属的量化索引区间来识别水印信息。因其量化步长与不可感知性成负相关关系，与鲁棒性成正相关关系，所以准确控制步长能提高水印稳定性，其原理如下若存在1 bit水印(0,1)，选择两个量化器进行量化

Qi(x)=Qi(x-di)+di

(6)

其中，Qi(x)=q[x/q],d是量化步长，d0=-q/4,d1=q/4。即

(7)

2 水印嵌入和提取算法

2.1 水印嵌入过程

水印嵌入框图如图1所示。

图1 水印嵌入框图

步骤如下:

(1)选取32×32对水印图像进行二值化处理；

(2)对512×512载体图像进行小波变换，提取第1层小波变换的系数HL1、LH1、HH1，分别对其系数矩阵进行分数阶傅里叶变换，变换阶次为(0.9，0.9)，提取其幅度矩阵A1、A2、A3；

(3)将幅度矩阵A1、A2、A3分别分为尺寸为8×8的无重叠块，对其子块进行QR分解，每个子块嵌入1bit水印信息，将对应的水印信息重复嵌入到R的第一行中，设置嵌入强度为d，根据公式

(8)

嵌入水印信息。其中R(1,j)为R第1行第j列元素，R′(1,j)为嵌入水印后R第1行第j列元素；

2.2 水印提取算法

本文算法是一种盲水印算法，提取步骤如下:

(1)对已受到攻击的水印图像进行相同层次的小波变换，提取第1层小波变换的系数HL1、LH1、HH1，分别对其系数矩阵进行分数阶傅里叶变换，变换阶次为(0.9,0.9)，提取其幅度矩阵B1、B2、B3；

(2)将幅度矩阵B1、B2、B3分别分为尺寸为8×8的无重叠块，每个子块提取1 bit水印信息；

(3)对B1、B2、B3子块进行QR分解，根据对应的R第一行元素重复提取水印信息，水印提取公式

watermarking′=arg min‖R′(1,j)-Qm(R′(1,j))‖,
m∈{0,1}

(9)

对每个R子块第一行8个元素进行水印提取，水印结果最终由多数原则确定，得到水印信息W1、W2、W3；

(4)将水印信息W1、W2、W3每个元素进行统计，由多数原则确定二值信息，最后得到提取水印信息W。

3 实验与分析

为了验证本文提出的基于DWT-FRFT变换和QR分解的盲数字水印算法的不可感知性和鲁棒性，本文利用MATLAB进行仿真，载体图像选用512×512的woman图像，水印为32×32的二值图像。

3.1 不可感知性测试

为了客观描述水印图像的不可感知性，本文采用峰值信噪比(Peak Signal To Noise Ration，PSNR)来评价，公式定义如下

(10)

式中,H(x,y)为原始图像，H′(x,y)为嵌入水印后的图像，PSNR越大，不可感知性越好。新算法结果同传统方法及文献方法所得结果进行对比，如表1所示。

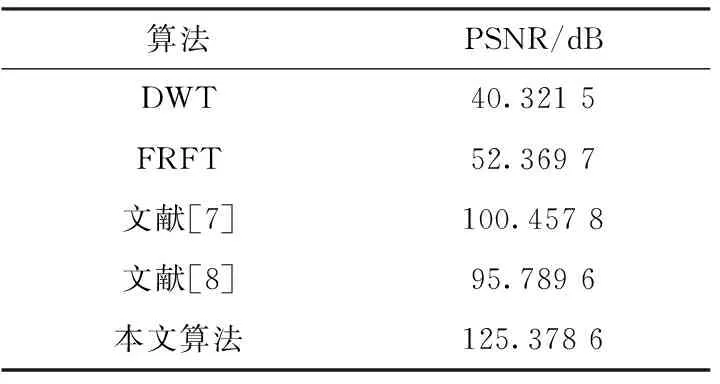
表1 不同算法下PSNR结果

图2 实验仿真图像

从仿真图像直观可知本文方法不可感知性良好，对比客观数据可知，本文方法不可感知性最优。

3.2 鲁棒性测试

为了客观描述本文算法的鲁棒性，采用归一化相关系数(NC)来评价，定义如下

(11)

式中，W(i,j)为嵌入的水印图像，W′(i,j)为提取的水印图像。

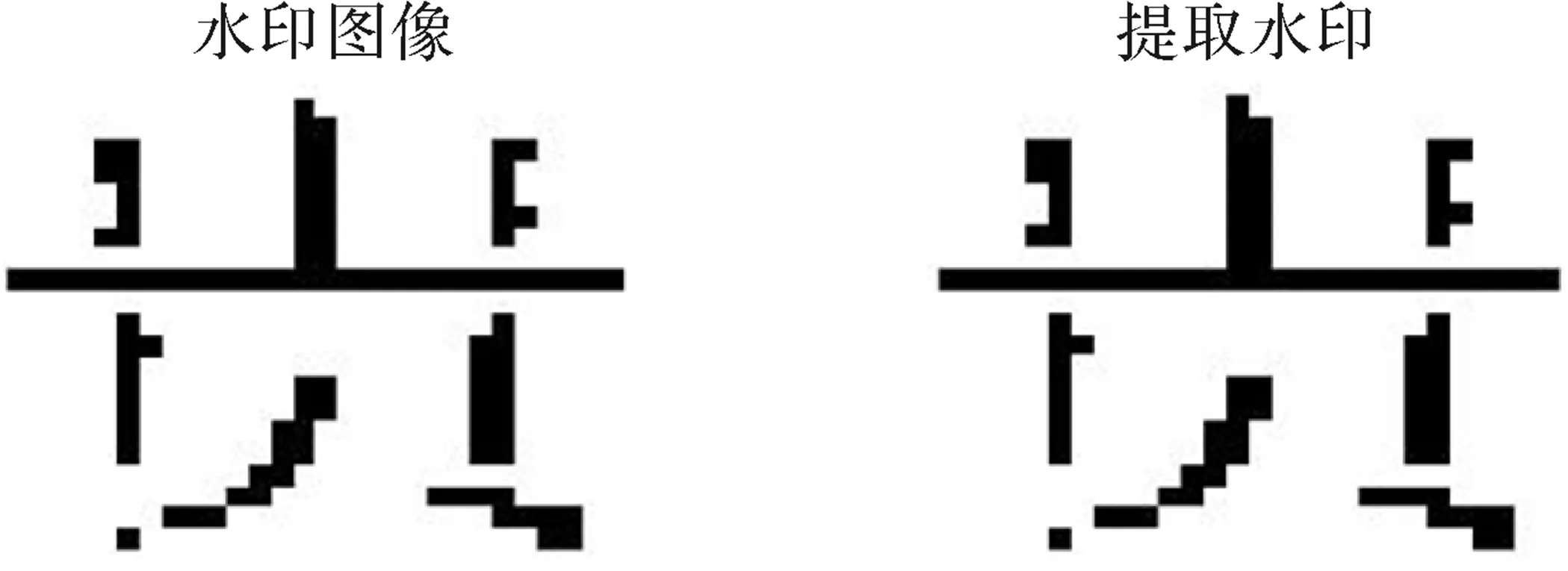
图3 未受攻击水印提取图像

现对含水印的载体图像进行1/4剪切、JPEG压缩、添加高斯噪声、旋转等操作，实验结果如下

图4 攻击后水印检测图像

从图像主观可知本文方法抗剪切性最强，抗噪声性较弱。为了客观评价本文方法，采用不同方法添加水印，攻击后进行水印提取，比较其NC，结果如表2所示。

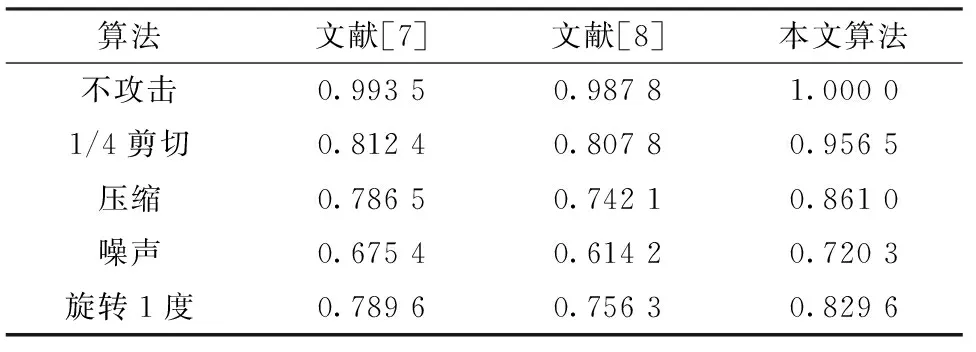
表2 攻击下不同算法的NC结果

比较可知，本文算法在常见攻击下，NC值均是最优，同文献方法所得结果相比，鲁棒性更强。

4 结束语

基于图像版权保护问题，本文提出了DWT-FRFT变换和QR分解的盲数字水印算法。该算法是将数字图像进行DWT-FRFT变换，获得低频子带，并进行分块QR分解，随后将水印信息重复嵌入R第一行。实验表明，本文方法具有良好的不可感知性和鲁棒性，优于传统方法。