基于粒子群优化BP网络的山区高速公路交通事故预测模型

季 芳，熊 坚，杨文臣，郭凤香

(1.昆明理工大学 交通工程学院，云南 昆明 650500；2.云南省交通规划设计研究院，云南 昆明 650500)

随着我国山区高速公路里程的不断增长，山区高速公路的交通安全状况引起人们的重视。大量研究表明，人是致使高速公路交通事故发生的主要因素。但不可否认的是，仍存在由道路线形条件复杂、天气状况恶劣等其他因素直接或间接导致的大量交通事故。因此，研究山区高速公路的交通事故预测模型具有重大的实用价值[1-4]。鉴于此，本文期望可以从现有的大量山区高路公路的交通事故记录中，通过对非人为因素的分析，来预测山区高速公路的交通事故。从而更好地识别山区高速公路上的高危路段，给予驾驶人更全面的驾驶提醒，提高山区高速公路的安全性。

传统的一些预测模型，包括概率预测法、贝叶斯预测模型等。在山区高速公路这一复杂的系统中，其在研究多个因素对交通事故的影响方面均存在不足，无法做出有效的预测[5-7]。此外，山区高速公路的事故发生存在较大的随机性，各影响因素与事故间不存在严格的线性关系。因此，需要选择一些用于非线性关系研究模型来做预测。本文采用基于粒子群优化的BP网络建立了山区高速公路的事故严重等级的预测模型，并基于昆石高速公路的事故数据对模型进行验证。

1 粒子群优化的BP算法

1.1 粒子群算法的原理

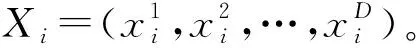
粒子群中的粒子所在的位置在不断地更新，是根据下列公式进行位置移动的

(1)

(2)

式中，i=1,2,…,m；d=1,2,…,D；w是一个非负数，是粒子群的惯性因子；加速常数c1和c2均为非负常数，一般取值为2；r1和r2是[0，1]范围内随机变换的一个随机数值；α为粒子群的约束因子，调控粒子速度的权重[10]。

1.2 粒子群优化的BP网络

BP算法自身存在以下不足：(1)BP算法的收敛速度偏慢，尤其当训练样本的数量极为庞大时；(2)存在局部最优问题，导致整体学习和训练结果不佳。因此，用粒子群算法优化神经网络的学习算法，弥补BP网络的不足，并提高BP网络的收敛速度及网络的学习能力。

基于粒子群优化的BP神经网络，如图1所示。

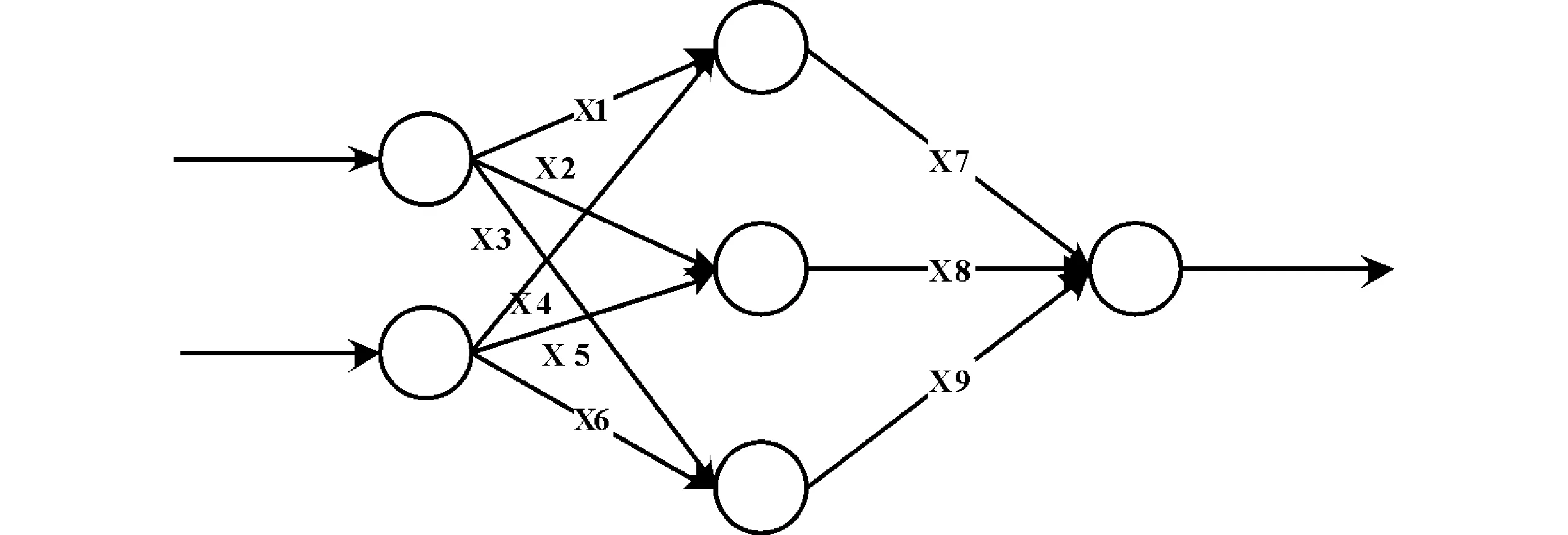
图1 基于粒子群优化的BP网络结构图

2 交通事故预测模型建立

2.1 输入层、输出层变量的确定

(1)输入层变量。输入层变量主要包括一些对交通事故严重程度有着紧密联系的影响因素，当然不是所有的影响因素均能够作为输入层的变量，变量的选取也需要结合实际的数据情况[11]。综合实际事故记录情况，确定以下5个变量为BP网络模型的输入层变量：1)时间：据夜间事故死亡率的分析显示：高速公路夜间的交通事故率比白天大1～1.5倍；2)天气：根据云南的气候情况和所记录的事故数据分析，本文的天气情况主要包括：晴、阴、雨、雾4类；3)车辆类型：发生事故时车辆的数目是随机的，车辆类型也难以做出一个统一的判定，本文在处理该问题时，采用了肇事车辆的车型来量化这一影响因素；4)道路平曲线半径：道路平曲线半径设计不当是发生交通事故的主要原因之一，本文将道路平曲线半径分为4个等级；5)道路纵坡坡度：纵坡坡度过大时，需要保持车辆的合理速度，维持连贯的驾驶状态将对行车安全造成较大的影响。相关研究表明，在长下坡极易发生交通事故。

(2)输出层变量。为了分析输入因素对事故的影响，将事故严重等级作为输出变量。基于昆石高速公路的事故记录情况，选择事故的伤亡人员数作为事故严重等级的衡量标准。根据相关事故等级的划分标准，本文将事故严重等级量化为0,1,2,3这4个等级：1)轻微事故：轻伤1～2人，财产损失机动车事故不足1 000元；2)一般事故：重伤1～2人，或轻伤3人以上，财产损失不足3万元；3)重大事故：死亡1～2人，或者重伤3人以上10人以下，财产损失3万元以上不足6万元；4)特大事故：死亡3人以上，或者重伤11人以上，同时重伤8人以上或者死亡2人，同时重伤5人以上，财产损失6万元以上。

在考虑事故严重等级时，为了让输出的结果能够有一个统一的量化标准。在本文的研究中，事故的严重程度还是以人员伤亡情况作为主要衡量标准的。因财产损失存在一定的估计，采用伤亡人员数作为衡量标准同时也体现了安全为第一的原则。

2.2 输入层、输出层的数据量化

事故数据的记录，大多为文字记录，难以直接应用于事故预测模型。根据本文所采用的BP网络模型的需要，对这些数据进行了量化处理[12]。在数据整理筛选完毕后，基于所选的312个抽样数据来建立模型。基于此，对数据的量化处理是本文事故数据处理的主要工作。具体的变量量化情况，如表1所示。

表1 变量的量化

3 模型仿真验证

3.1 模型的网络训练和测试

鉴于MATLAB神经网络工具箱的方便实用，本文采用它来实现该网络。将神经网络的均方误差作为粒子群算法的适应度，适应度的计算通过调用子函数来实现[13-16]具体神经网络模型的实现过程，如图2所示。可见网络的模型建立，是通过5个输入层的输入变量，经过隐含层，来实现输出层的1个变量的输出。

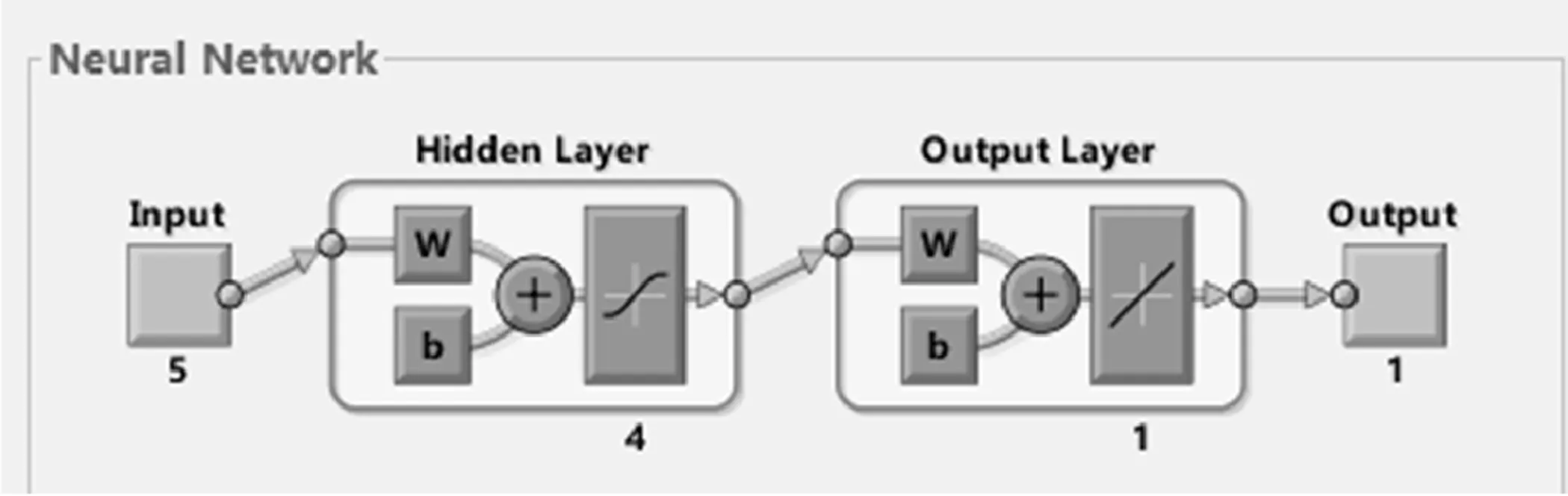
图2 神经网络模型的实现过程

完成编程后，对数据进行神经网络的训练以及测试。本文以昆石高速公路K0～K78路段，2008年～2012年之间的312条事故数据为样本数据。并随机抽取样本数据中的260条作为模型的训练数据，将剩下的52条作为测试数据进行模型验证。通过不断迭代，使数据训练的效果达到较佳水平。最终网络的训练结果，如图3所示。

图3 均方误差(MSE)变化趋势图

由图可见，PSO-BP的网络收敛速度比BP的收敛速度快，且PSO-BP最后达到的网络均方误差值也相较BP更小，这也体现了粒子群算法的优化效果。基本上迭代至第6代以后，PSO-BP网络的误差已趋于收敛，而不加优化的BP网络还未呈现出明显的收敛趋势。同时，还可以看出在多次迭代之后，PSO-BP的网络误差值明显低于BP网络的误差值。

经过网络的迭代训练，最终的网络训练集和测试集误差如表2所示。

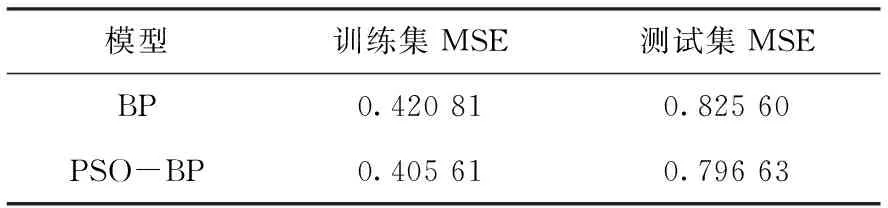
表2 整体网络误差对比表

从表2可得出结论：(1)PSO-BP模型的总体误差比BP模型小；(2)两个模型的训练集误差均比测试集误差小。这是因训练集的误差是模型经过多次迭代而来的，而测试集的误差是将测试集的数据直接放入模型进行的验证，不存在迭代，是一次验证而出的结果。

将样本中所取的52条测试数据放入模型进行验证，该52条测试数据所验证的模型的预测准确率为89.6%。这一验证结果说明，所建立的预测模型可用作事故严重等级的预测分析。

3.2 模型仿真结果分析

所建立的模型在上一节通过验证且准确率较佳，故在预测模型的基础上，进行仿真模拟分析，研究单个影响因素与事故严重程度间的关系，以期得到一定的事故发生规律。

在所有的仿真结果分析中，均给出统一的情境设定，5个输入层变量定为：凌晨；晴天；重型货车；半径为600～2 000 m；坡度取值区间为[-5，-3)；所设定的情境输入层数据量化后为：(0，0，4，0，1)。

(1)时间-事故的预测分析。在时间-事故的输入输出关系研究中，设定的情境输入层数据量化为：(*，0，4，0，1)，通过模型的仿真模拟，得出事故严重等级预测值，据此进行时间-事故间的关系分析。程序运行后，模型的预测结果如图4所示。

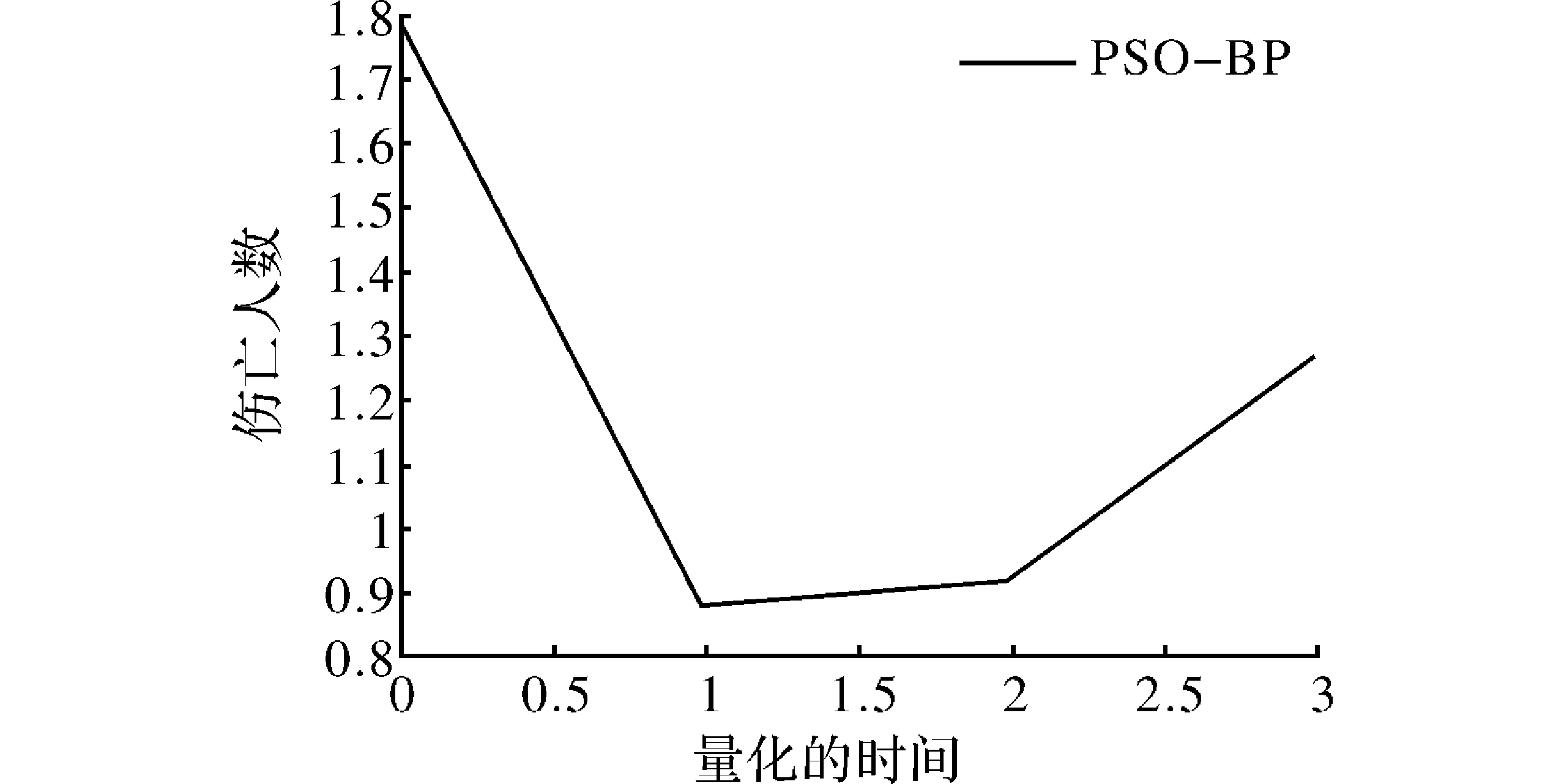
图4 时间与伤亡人数的量化关系图

图4中，横坐标为量化的时间，为0～3，表征凌晨、上午、下午、晚上这4个时间段；纵坐标为量化的伤亡人员数，表征事故的严重等级。发现在时间段0，即凌晨0:00～8:00；其次在时间段3，也就是晚上的18:00～0:00，事故的严重等级预测值较高，模型预测在这两个时间段更易发生严重的交通事故。这一现象的可能原因是在深夜与凌晨这两个时间段，驾驶人更易出现疲劳驾驶以及货车存在的超载现象，导致较为严重的事故发生。

(2)天气-事故的预测分析。在天气-事故的输入输出关系研究中，设定的情境输入层数据量化为：(0，*，4，0，1)。通过模型的仿真模拟，得出事故严重等级预测值，据此进行天气-事故间的关系分析。程序运行后，模型的预测结果如图5所示。

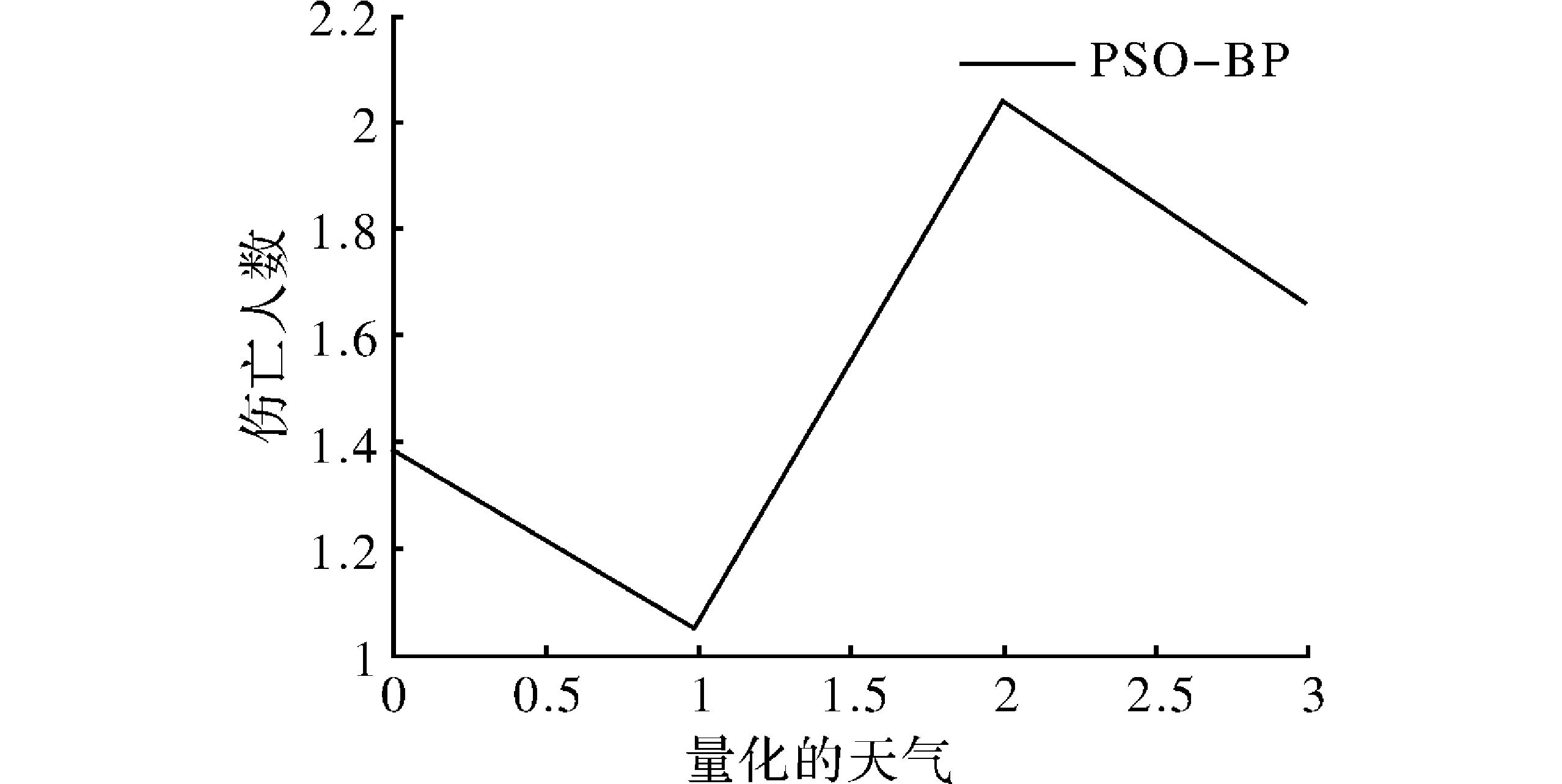
图5 天气与伤亡人数的量化关系图

图5中，横坐标为量化的天气，赋值为0～3，表征晴、阴、雨、雾这4种天气状况；纵坐标为量化的伤亡人员数，表征事故的严重等级。可以看出，在天气情况为2和3时，也就是雨天与雾天的天气状况下，事故的严重等级预测值较高，模型预测在雨天及雾天更易发生严重的交通事故。这一现象可能的原因是因为在高速公路上的车辆行驶车速较高，雨天状况下路表摩擦降低，更易发生事故；雾天状况下，驾驶人的视觉观察能力受限，极易导致多车追尾事故，致使重大事故的发生。

(3)半径-事故的预测分析。在半径-事故的输入输出关系研究中，设定的情境输入层数据量化为：(0，0，4，0，*)。通过模型的仿真模拟，得出事故严重等级预测值，据此进行半径-事故间的关系分析。程序运行后，模型预测结果如图6所示。

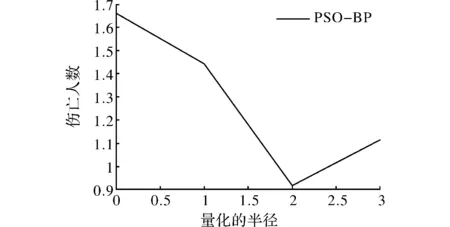
图6 半径与伤亡人数的量化关系图

图6中，横坐标为量化的半径，赋值为0～3，表征4种半径的取值范围；纵坐标为量化的伤亡人员数，表征事故的严重等级。可见，在半径编号为0和1时，即在半径取值范围为0～600 m和600～1 500 m时，事故的严重等级预测值均较高，模型预测在这两个半径取值范围内的地点更易发生严重的交通事故。这一现象可能的原因是在小半径处，尤其是曲线半径骤然变小时，若保持原有的行车速度，易发生侧翻事故，导致严重事故的发生。

(4)车辆类型-事故的预测分析。在车辆类型-事故的输入输出关系研究中，设定的情境输入层数据量化为：(0，0，*，0，1)。通过模型的仿真模拟，得出事故严重等级预测值，进行车辆-事故的关系分析。程序运行后，模型预测结果如图7所示。

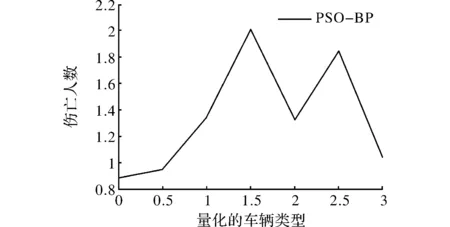
图7 车辆类型与伤亡人数的量化关系图

图7中，横坐标为量化的车辆类型，赋值为0～6，表征7种类型的肇事车辆；纵坐标为量化的伤亡人员数，表征事故的严重等级。可以看出，在车辆类型编号为3和5时，即在车辆为重型货车和汽车列车的情况下，事故的严重等级预测值较高，模型预测这两类车型更易发生严重的事故。这一现象可能的原因是在山区高速公路上，重型货车和汽车列车的装载大且车速较快。尤其与客车发生碰撞时，极易造成人员伤亡，致使严重事故的发生。

4 结束语

本文采用基于粒子群优化的BP网络建立了山区高速公路的事故严重等级的预测模型，并基于昆石高速公路的事故数据对模型进行验证。经验证，模型的预测效果较佳。预测准确率为89.6%后，通过设定情境，用模型进行仿真分析，得出了一些事故发生规律。仿真结果表明：在凌晨时段、雨雾天、以及在小半径处，驾驶重型货车等情况下，更易发生严重的事故，这就需要驾驶人在这些情况下更加注重行车安全。