一种核相关滤波器的多尺度目标跟踪方法

李远状，韩彦芳，于书盼

(上海理工大学 光电信息与计算机工程学院，上海 200093)

目标跟踪是机器视觉领域中一项应用广泛的重要课题，其在视频监控、医学成像、机器人视觉、安防等应用中都扮演着重要的角色[1]。虽然目标跟踪在近年来取得了明显的进展，但如光照变化、尺度变化、快速运动和遮挡等问题[2]并没有得到有效解决。

基于判别式分类器的单目标跟踪算法是近几年的主流算法，与传统的跟踪算法相比其跟踪的性能和精度有显著提升。基于判别式跟踪算法有核结构化输出跟踪(Structured output tracking with kernel，Struck)[3]算法、多样例学习(Multiple Instance Learning，MIL)[4]跟踪算法、跟踪-学习-检测(Tracking Learning Detection，TLD)[5]跟踪算法等。这些算法将目标跟踪看成一个分类问题处理，对已有目标图像的周围进行采样，通过判断样本是背景还是目标将样本划分为正负样本利用在线或离线的方式训练分类器，再用训练好的分类器检测候选样本得到目标位置。然而，受限于这些算法的采样方式，训练样本和候选样本数量有限，无法得到分类精度较高的分类器，并且跟踪性能明显不足。Bolme 等[6]提出一种最小平方误差和输出(Minimum Output Sum of Squared Error，MOSSE)跟踪算法，该算法提高了上述算法的运算效率，然而有限的候选样本还是限制了其跟踪性能。Henriques 等[7]提出核循环结构检测跟踪(Circulant Structure of tracking-by-detection with kernel，CSK)跟踪算法，该算法通过对单个样本进行循环移位得到了大量的训练样本。使用同样的方法也可以得到大量的候选样本，弥补了大多数算法的不足，同时计算过程变换在频域实现了快速计算。之后同一作者在CSK的基础上提出了核相关滤波器(Kernelized Correlation Filter，KCF)[8]跟踪算法，该算法使用梯度方向直方图(Histogram of Oriented Gradients，HOG)[9]特征对CSK算法进行了改进。然而，上述跟踪算法着重于怼目标位置的估计，并没有解决跟踪过程中目标尺度变化的问题，无法实现对目标尺度变化显著的视频中目标的有效跟踪。

因此，针对KCF跟踪算法不能自适应目标尺度变化的缺点，本文在KCF跟踪算法的基础上提出了一种多尺度匹配的尺度估计方法，实现了尺度自适应的目标跟踪。同时在目标跟踪数据集中选取10组尺度变化剧烈的视频序列对算法进行验证，并与KCF、DSST、CN等优秀跟踪算法的结果进行了对比。

1 KCF跟踪算法

KCF跟踪算法的核心思想是利用置换矩阵对基样本进行循环移位，并对目标区域密集采样得到大量的样本来训练分类器。利用核函数和分类器计算候选区域与目标区域的相似概率值，选取最大值对应的位置作为更新的目标位置，同时训练的样本具有循环特性，可以将样本对角化并转换到频域进行计算，跟踪速度得到较大的提升。算法主要部分为循环采样、训练分类器及快速检测。

1.1 训练核岭回归分类器

岭回归的目的是利用训练样本{xi,yi}找到一个函数 来使代价函数即平方误差最小化。其中xi为图像样本，yi为回归目标，z为待检测图像块，θ为分类器参数，训练过程可用下面公式描述

(1)

式中，λ为防止过拟合的正则化参数，训练的目的是找到最优的θ使代价函数式(1)最小。

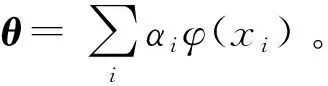
由核方法可知核函数在原始特征空间的计算值可以表示高维空间的样本特征的点积，其中核函数为多项式核和高斯核，即k(x,x′)=φT(x)φ(x′)。由上可知优化对象由θ转换到α，并且响应函数可以表示为

(2)

所有样本之间的点积组成n×n的核矩阵Kij=k(xi,xj)，由式(1)和式(2)可求得

α=(K+λI)-1y

(3)

式中，α是由αi组成的向量，K为核矩阵，I为单位矩阵，y是由yi组成的向量。

1.2 循环矩阵

由于训练分类器需要大量的样本，因此KCF算法在目标区域利用循环矩阵进行循环移位。整个训练过程只需一张有目标的样本图像即基样本x，循环移位得到的样本称为负样本。以一维信号为例来循环移位，这些结果同样可以应用到二维图像上面。记基样本为目标图像块的n×1向量，x=[x1,x2,x3,…,xn]T，通过置换矩阵P对基样本进行循环移位，基样本移位一次的结果Px=[xn,x1,x2,…,xn-1]T，可以看出移位后的所有样本集合为{Pux|u=0,1,…,n-1}。将移位后的所有样本重新组合得到循环矩阵X

(4)

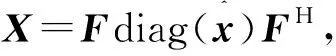
1.3 快速检测

由于核矩阵K=C(kxx)也是循环矩阵及其可对角化的特性，结合式(3)可求得

(5)

其中kxx是核矩阵的第一行元素。

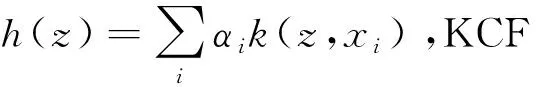
(6)

h(z)是一个向量，其每个元素值就是候选区域与跟踪目标相似概率值，因此h(z)最大元素值所对应的位置即为跟踪目标的位置。

2 尺度自适应KCF跟踪算法

由于传统的KCF跟踪方法使用固定的尺度窗口来跟踪目标，当目标发生明显的尺度变换时，后续的特征和分类器更新会出现信息丢失的问题，导致算法不能有效的跟踪目标，甚至会因为尺度不匹配造成误差累计造成跟踪目标丢失。因此，将尺度估计加入到传统的KCF跟踪算法中对完善跟踪目标是非常必要的。文献[13]和[14]提出了一种基于CSK跟踪算法的尺度自适应改进算法，基于此算法，本文提出了一种候选目标尺度池与目标匹配机制。该算法的核心思路是通过缩放候选目标与跟踪目标做相似度匹配，找出可信度最高的中心点作为下一帧的跟踪目标，以实现目标的尺度估计。

2.1 候选目标尺度池

在传统的KCF跟踪算法已算出分类器α的基础下构造候选目标图像尺度池。设候选目标图像zm尺寸为M×N，scale={a1,a2,…,an}表示候选目标尺度池，其中ai(i=1,…,n)表示尺度因子。通过缩放图像建立多尺度候选目标序列，因此可以得到多尺度候选目标尺寸aiM×aiN，候选目标图像序列zmk为

zmk=scale*=zm=ai*zm(k,i=1,2,…,n)

(7)

其中ai>1表示放大候选目标图像，ai<1表示缩小候选目标图像，尺度缩放函数是基于双线性插值[15]的函数。

利用固定的窗口尺寸在候选目标图像序列zmk上截取候选目标序列zk，缩放过程中采样窗口中心点坐标的变化与尺度池的变化保持一致。

2.2 位置与尺度估计

利用候选目标序列和训练的分类器、响应函数来进行目标位置和尺度的检测，由式(6)可知每一个候选目标尺度都会得到一个响应向量。响应值的范围取决于样本标签y的形式。本文采用的标签形式与KCF跟踪算法一样，为从0到1的连续标签形式。此标签值相当于该点是目标的概率值，目标中心标签为1，离目标越远的点标签值越低，最终递减到0，计算公式如下

yij=exp(-((i-i′)2+(j-j′)2)/s2)
∀i,j=0,1,…,n-1

(8)

其中(i′ ,j′)是目标中心位置，参数s为空间带宽，yij表示点(i,j)的标签值，相比样本的二值标签的形式，连续标签形式使跟踪目标的位置更加准确。

根据式(6)，可得出多尺度目标响应函数

(9)

其中，zk是候选目标序列，α是训练的分类器参数，该响应值序列代表成为目标的可信度矩阵序列，找出矩阵序列中最大元素值对应的尺度因子S和坐标位置pos。由于是通过缩放候选图像来匹配最佳位置与尺寸，因此得到的数据要进行逆变换，所以候选目标的尺度因子为1/S，目标的坐标位置为1/S×pos。

假设取候选目标尺度scale={0.8,0.9,1,1.1,1.2}，先通过缩放函数将候选目标按照尺度池进行缩放得到候选目标序列，再通过核相关滤波分类器与上一帧目标图像计算响应值，得到相应的5个响应矩阵。找出其中最大的响应值所对应的尺度，即可计算出目标最佳尺寸。目标的位置由最大响应值对应的位置计算得到，此过程可以得到目标实时的尺度与位置信息，跟踪算法流程如表1所示。

2.3 目标模板更新

分类器与目标外观模板的更新由跟踪得到的新样本及前一帧的参数决定，一般给两者不一样的权值进行线性组合。当有目标发生尺度变化时，需要将前一帧的参数先缩放到与新目标同样的尺寸，再进行线性组合。更新策略中目标外观模板和分类器系数为

(10)

(11)

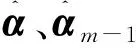
表1 本文算法流程

3 实验与分析

为了评估提出的跟踪算法的性能和效率，在跟踪视频数据集中选取多组尺度变化明显的视频进行大量的实验评估。文中选择重叠率(Overlap Precision，OP)、中心位置误差(Center Location Error，CLE)及跟踪速度(Frames Per Second，FPS)3个指标进行定性分析，并画出距离精度曲线(Distance Precision，DP)来分析跟踪效果。同时，本研究选取了包括CN、CT、DSST、STC、KCF、MOSSE等多种优秀算法进行跟踪效果对比，所有对比试验在同一实验环境下进行。

3.1 实验配置及参数设置

实验硬件配置环境为Intel Core i5-6267U CPU，主频2.9 GHz，4 GB内存，软件环境为MATLAB R2012b。文中参数设定为高斯核函数标准差σ=0.5，学习率β=0.02，正则化参数λ=10-4，空间带宽s=0.1。由于每帧图像之间的尺度变化不大，因此尺度因子不能选过大，否则无法正确匹配到相应的尺寸。由此，设定尺度步长为0.03，候选目标尺度等级为5，尺度池scale={0.94，0.97，1，1.03，1.06}。该算法采用方向梯度直方图(Histogram of Oriented Gradient，HOG)特征来表征图像，该特征在大多场景下效果突出，采取8×8像素为一个cell，2×2 cell为一个block，其中block以8个像素为步长遍历整个图像。

3.2 实验结果分析

从视频集中选取10组具有代表性的尺度变化剧烈的测试序列作为实验对象，用改进算法和其他7组优秀算法对比测试这10组序列，得到CLE、OP及其平均值，结果分别如表2和表3所示，其中最佳值标记为粗体。实验数据表明，改进算法对大多数测试视频序列的跟踪效果表现突出，并且相比其他算法，该算法CLE与OP指标平均值排名最高。对比尺度自适应的DSST算法，CLE平均减少了13%，OP平均增加了10%，可见多尺度跟踪效果明显。实验绘制了3组序列的跟踪精度曲线，具体结果如图1所示。

表2 平均中心位置误差 /pixel

表3 重叠率 /%

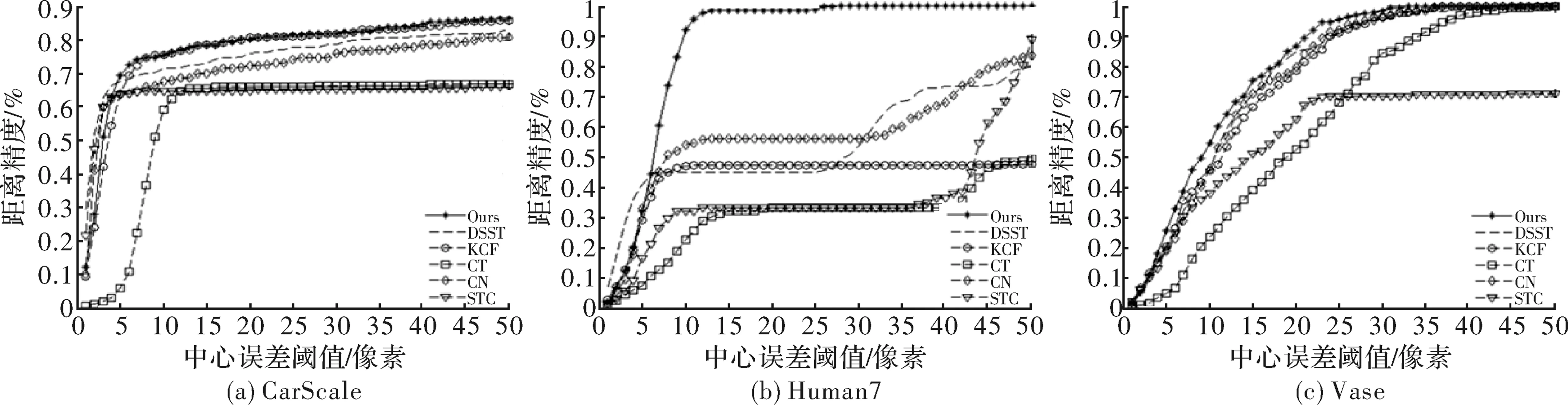
图1 跟踪精度曲线

文中所提算法是在KCF算法基础上加以改进，可以达到目标尺度框自适应变化的效果，解决目标丢失的问题。从跟踪精度曲线可以看出改进算法的跟踪精度总体上优于KCF算法，说明了该算法在保证原算法优点的同时，通过多尺度跟踪进一步提高了跟踪精度。文中给出了与KCF、DSST处理速度对比的结果，如表3所示。虽然新算法与传统KCF相比跟踪速度有所下降，但是并没有影响视频的流畅度，仍然可以保证实时跟踪；而与尺度自适应DSST算法相比，新算法的跟踪速度有较大提升。

表3 平均跟踪速度

图2列出了更为直观的对比，实验选取了4组视频序列的部分帧数，对比了6种算法的跟踪结果。从数据中可以看出，改进算法在尺度变化序列中的整体表现优于其他算法，实现了目标尺度自适应跟踪。

图2 6种算法的跟踪结果

4 结束语

针对传统的核相关滤波器(KCF)跟踪算法没有解决目标尺度变化并导致目标丢失的缺点，提出了一种利用候选目标尺度池与目标匹配的机制，并解决了跟踪算法无法适应目标尺度变化的问题。与KCF等优秀跟踪算法比较实验表明，提出的算法弥补了KCF算法无法改变尺度的缺陷，并有效的解决目标丢失的问题，提升了目标跟踪精度。