基于磁定位的手术异物遗留检测技术研究

郑建立，卢祥林，夏宇彬

(上海理工大学 医疗器械与食品学院，上海 200093)

手术异物遗留(Retained Surgical Items，RSIS)是指任何手术操作后遗留在患者体内的物体，这些遗留异物不仅会对患者健康造成严重的影响，同时也给患者带来额外的经济负担。手术中最常见的遗留物体有：软质物品(如海绵、纱布)、小件物品、针头及其他锐器。在这些遗留物体中，手术纱布是最常见的残留异物，因为它们在浸透血液后很难被发现。文献[1]的数据显示，纱布数量约占总遗留异物数量的69%。一般为防止手术器械和纱布的遗留，外科医生和手术室工作人员主要依靠“清理腹腔”、手工清点器械和纱布等计数，但在排查过程中容易出现人为错误，导致异物遗留的发生。

目前有采用RFID(Radio Frequency IDentification)技术的智能纱布，可以实现精确的计数以及对患者体内有无残留的纱布进行判断。但是这种技术的成本较高，也无法获得纱布的准确位置，并且还需要医生手动植入RFID标签，因此并没有得到很好的推广。

为了能够实现定位，医学上常用的方法有超声波[2]、射频[3]和磁感应定位[4-5]。射频和超声波定位都是通过有源设备向外界发射信号以达到定位目的。但是，这两种方法并不适用于接触血液的纱布。文献[4,6]提出的磁感应定位方法使用的是无源器件永磁体，虽适用于本文的场景，但也只是针对单个目标进行定位。文献[7]提出利用模拟器件采集数据后再A/D转换的方式，这种方法需要自行设计电路，而且会产生较大的噪声干扰。

本文提出了基于全新的数字三轴传感器的定位方法，该方法采用新的非线性最优化方法，提高了定位的精度，降低了算法耗时，并且可实现最多4个目标的定位。

1 磁定位数学模型

当永磁体与传感器之间的距离远大于永磁体的大小时，可以将永磁体视为一个磁偶极子模型。则距离永磁体距离为R处的磁感应强度B可由如下公式计算[8]

(1)

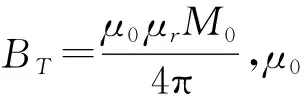
如果令磁矩方向H与z轴正方向的夹角为θ[4]，其在xy平面的投影与x轴正方向的夹角为φ，如图1所示，则H又可以表示为[sinθ·cosφ,sinθ·cosφ,cosθ]T。

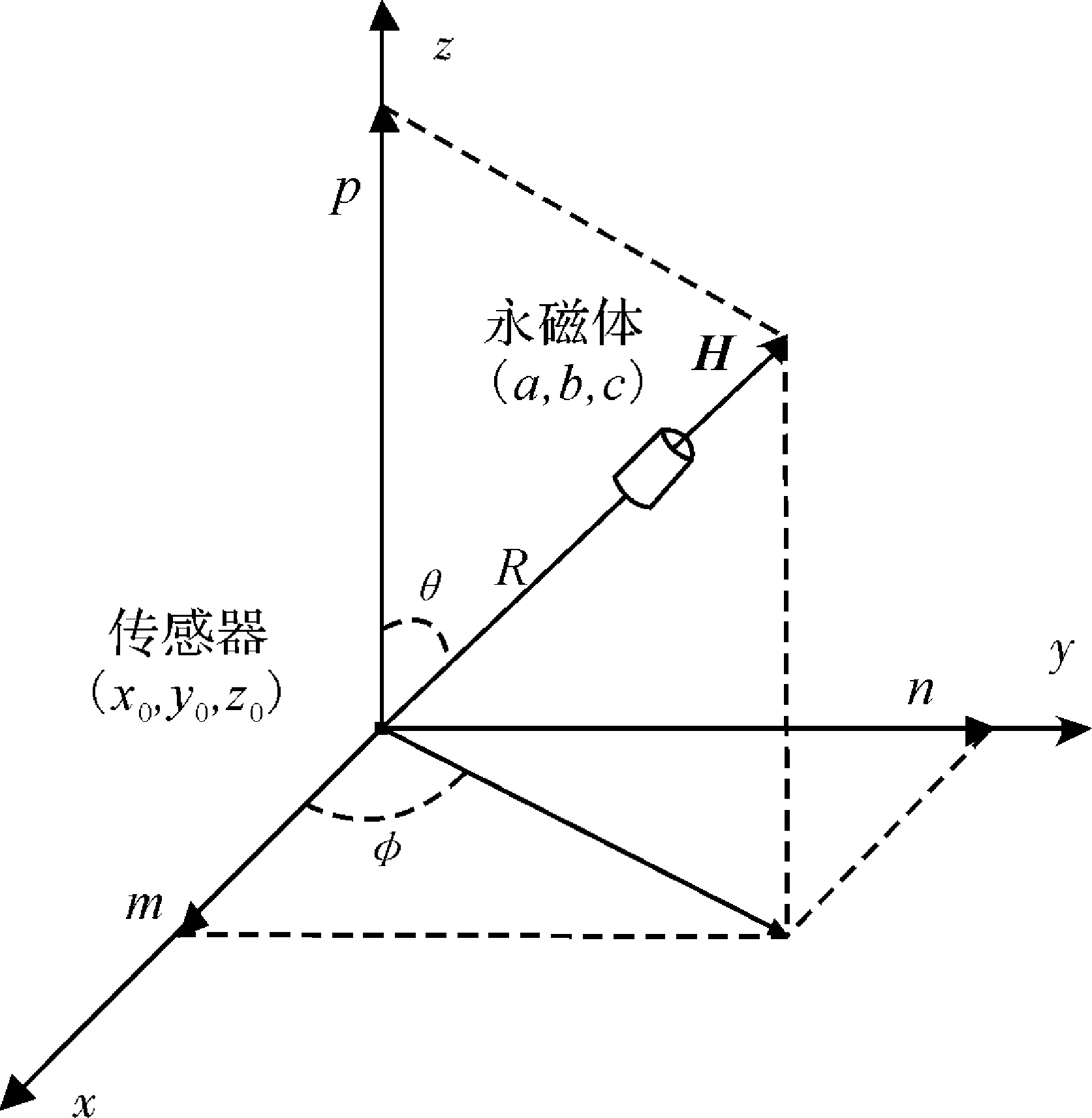
图1 磁偶极子与传感器

通过空间中多个传感器测得的数据，结合式(1)就可以联立方程求解得到永磁体的位置坐标(a,b,c)与角度(θ,φ)，求解算法将在后文中介绍。

2 磁定位硬件设计

磁定位硬件由3个部分组成：传感器阵列、Arduino Mega 2560开发板和上位机，其组成关系如图2所示。Arduino上的程序通过I2C读取传感器数据并由串口发送给上位机，上位机软件根据数据计算并显示永磁体的位置。

图2 磁定位系统

传感器阵列由13个数字式三轴磁传感器组成，具体型号为Memsic 公司的MMC5883MA各向异性磁阻(Anisotropic Magneto Resistive，AMR)传感器，能够实现±8 Gauss量程16 bit工作模式下，±0.2% FSR 线性度，0.2% FSR磁滞，0.2% FSR重复性，以及0.25 mG的分辨率。其出色的性能为软硬件的抗干扰修正提供了更为快速的算法，带来了更为精确及快速的方向定位。如图3和图4所示，传感器阵列的大小为20 cm × 20 cm，传感器之间水平与垂直方向小的间隔为5 cm，大的间隔为10 cm。

图3 MMC5883MA磁传感器模块

图4 传感器阵列布局

Arduino通过2个8通道I2C双向开关(TCA9548A)与传感器阵列相连，如图5所示。因为Mega 2560上只有2个I2C接口，必须要通过类似TCA9548A的设备才能连接13个传感器。Arduino每次读取一个传感器的数据，然后发送给上位机，当其读取完13个传感器之后会从第1个再次读取，如此循环。

图5 Arduino与TCA9548A

3 磁定位求解算法

3.1 单个目标

每一个传感器测得的磁感应强度Bl=[Blx,Bly,Blz]T(l=1,2,…,13)，根据式(1)得出

(2)

式中，等号左边为测量值，等号右边为理论计算值。(xl,yl,zl)代表第l个传感器的位置坐标，为已知的自定义的参数；Rl为永磁体到第l个传感器的距离。在理想情况下，传感器的测量值应与式(1)的计算结果相等。但在实际中两者结果不可能完全相等，只能非常接近，因此，定义如下误差函数[10]

E=Ex+Ey+Ez

(3)

其中，Ex，Ey，Ez分别定义为

(4)

N为传感器的个数，Bmx、Bmy、Bmz分别为x、y、z3个方向的理论计算值，即式(2)等号的右边。

理论上误差函数E应该等于0，但实际中只能找到一个最接近0的最小值。通过求解E的最小值，进而得到永磁体的位置和角度。本文采用的求解方法为LM (Levenberg-Marquardt) 算法[9]。该算法收敛速度快，在MATLAB中平均耗时约为160 ms，而且在单个目标情况下不会陷入局部最优，能够得到正确结果。单目标定位中LM算法所用的初值为(a=0.1 m,b=0.1 m,c=-0.1 m,θ=0 rad,φ=0 rad)，即假设初值在传感器阵列上方0.2 m×0.2 m×0.2 m大小的立方体的中心位置。其中c=-0.1 m是因为传感器z轴的正方向是朝下的，若以传感器所在平面为零点，则其上方的值小于0。

3.2 多个目标

多个目标的求解思路与单目标一致，只不过每一个传感器测得的数据不再是单一磁体的磁感应强度，而是多个磁体的矢量叠加。测量值与理论计算值的对应关系如下[11]

(5)

式中，等式左边为测量值，右边为理论计算值；M代表目标永磁体的个数；(aq,bq,cq)代表第q个永磁体的位置坐标；(mq,nq,pq)代表第q个永磁体的磁矩方向；Rlq代表第q个永磁体与传感器的距离。

误差函数仍然为式(3)和式(4)，只是式(4)中的理论计算值Bmx、Bmy、Bmz不同，需要变为式(5)中等号的右边部分。多目标情况下，若没有一个合理的初值，只使用LM算法求解可能陷入局部最优，无法得到正确的位置坐标。因此，需要使用其他全局最优化方法。本文测试了免疫克隆粒子群算法[12]与人工蜂群算法(Artificial Bee Colony，ABC)[13]。实验发现，在有3～4个目标时，使用免疫克隆粒子群算法有较大可能得不到最优解。本文使用的是基于ABC算法改进的算法，叫做IGAL-ABC[13-15]。该算法能够避免陷入局部最优从而得到正确的位置坐标。但是该算法收敛速度比较慢，需要十几秒的时间。因此，初值的确定由IGAL-ABC算法来确定，之后结果以此初值为基础通过LM算法计算获得。

4 实验结果与分析

实验中使用的永磁体为直径8 mm、高度3 mm的Nd-Fe-B 磁体，定位软件在MATLABR2017a中实现。实验测得其磁矩大小为0.1356 m·A2。总误差Err定义如下

(6)

式中，(a,b,c)代表计算得到的位置坐标，(at,bt,ct)代表永磁体的真实位置坐标。

对于单个目标，本文计算了平面上同一位置不同高度的50次的定位误差，如6图所示。

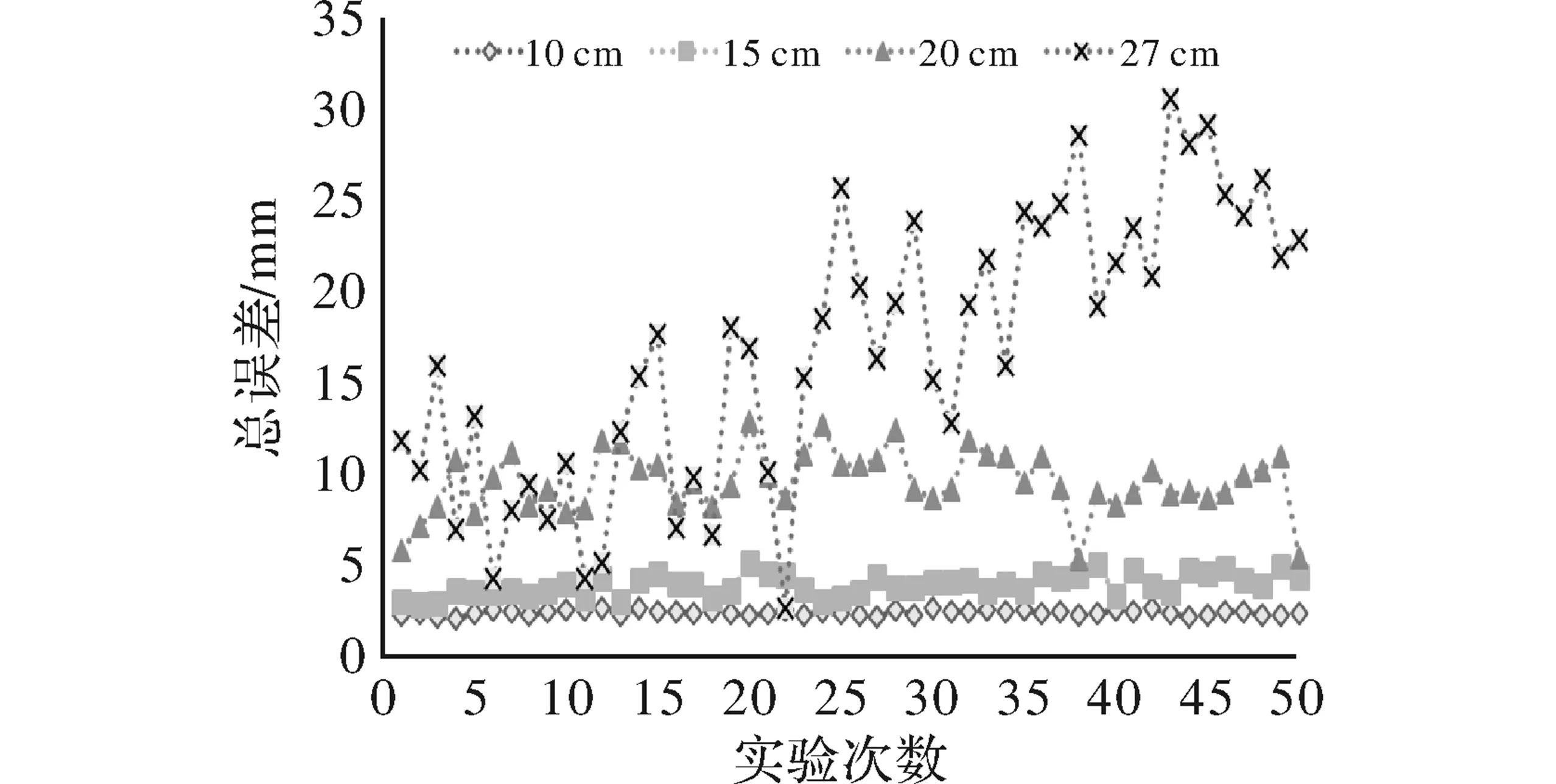
图6 不同高度的定位误差

从图6中可以看出，随着高度的增加，定位的误差和波动性逐渐增大。在10 cm、15 cm、20 cm和27 cm高度时的平均总误差分别为：2.44 mm、3.95 mm、9.52 mm和16.75 mm。究其原因，是因为高度越高，传感器位置的磁感应强度越弱，测得的数据准确度降低，而提高传感器的灵敏度则可以降低定位误差。

如前文所述，LM算法本身具有较快的收敛速度。如果LM算法的初值选取得当，即所选初值与真实值比较接近，则可以更进一步提高计算速度。因此，若将上一次的计算结果作为下一次LM算法的初值，则可以得到磁体的实时运动轨迹。实验中运用这种方式计算耗时在30～100 ms之间，具体数值取决于永磁体的个数。图7展示了两个目标的运动散点轨迹，其中圆的左右部分分别对应着2个磁体的运动轨迹。图8显示的是4个目标连续30次单点定位的结果。

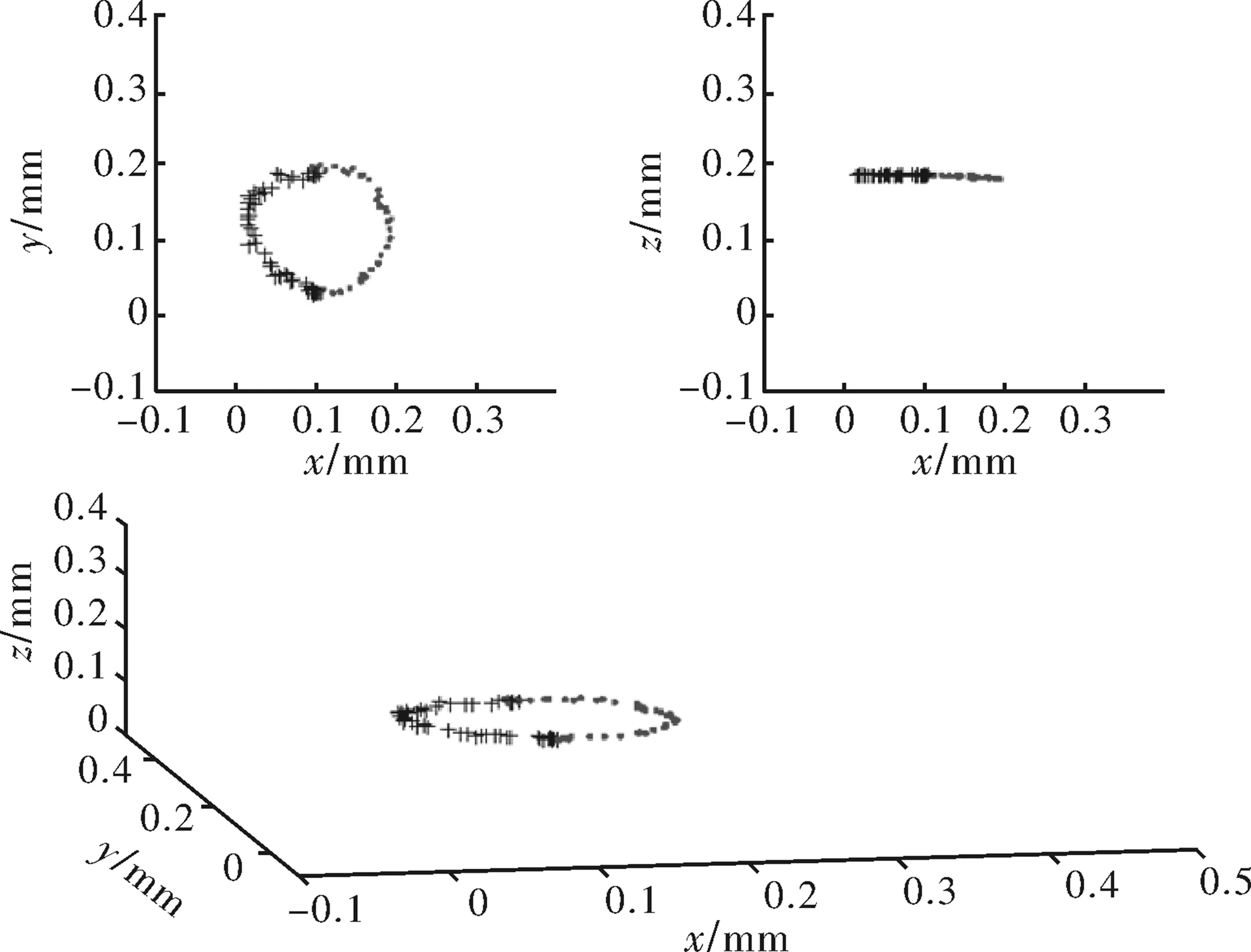
图7 两个目标轨迹

图8 4个目标定位

5 结束语

本文建立了多目标的永磁体实时定位系统，该系统在准备系统定位初值阶段耗时较长，需要约10～15 s时间(与目标数量有关)，其后的定位耗时均在100 ms以内。该系统还能够实现较大高度范围的定位，尽管不同高度定位误差有所差异，平均误差最小约为2.5 mm，最大约为17 mm，但都能满足实际要求。下一步的研究方向将集中在对更多目标的实施定位以及提高定位精度等方面，并计划将这套系统以嵌入式的方式实现，使其更加符合实际使用需求。