BET比表面积法在材料研究中的应用

何云鹏，杨水金

湖北师范大学化学化工学院，湖北黄石 435002

1938年 BRUNAUER等[1]基于Langmuir 单层吸附模型提出一种多分子层吸附理论，并推出相应的吸附等温式—BET方程。BET吸附等温式适用于物理吸附，是测定固体表面积的理论依据。基于BET公式测定吸附量和计算固体化表面积的方法也被称之为BET法。BET理论最大优势考虑到了由样品吸附能力不同带来的吸附层数之间的差异，这是与以往标样对比法最大的区别；但是人们仍对BET理论考虑表面的不均匀性、吸附质分子间的横向相互作用、各层吸附热均有不同、吸附层数有限[2-4]等局限性进行修正。

BET公式是现在行业中应用最广泛，测试结果可靠性最强的方法，几乎所有国内外的相关标准都是依据BET方程建立起来的。

1 BET吸附理论及BET公式

BRUNAUER等把Langmuir吸附等温式推广到多分子层吸附[5]。BET模型保留了Langmuir模型中吸附热与表面覆盖度无关和吸附分子间无相互作用的假设，又补充了：1)吸附可以是多分子层的，且不一定完全铺满单层后再铺其他层；2)第一层吸附是气体分子与固体表面直接作用，其吸附热(E1)与以后各层吸附热不同[6]；而第二层以后各层则是相同气体分子间的相互作用，各层吸附热都相同，为吸附质的液化热(EL)。据此模型，采用与Langmuir类似的动力学推导得到了BET公式[7]：

式中：p为氮气分压，Pa；p0为吸附温度下液氮的饱和蒸气压，Pa；Vm为样品上形成单分子层需要的气体量，mL；V为被吸附气体的总体积，mL；C为与吸附有关的常数。

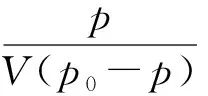
式中，Sg为被测样品的比表面积，m2/g；NA为阿伏伽德罗常数；Am为被吸附气体分子的截面积，nm2；m为被测样品质量，g。

通常BET公式适用的相对压力0.05～0.35之间，C值为3～1 000。一般地，以氮气为吸附质，在金属、聚合物和有机物上，C值在2～50之间；氧化物和二氧化硅上，C值在50～200；在活性炭和分子筛等强吸附剂上，C值大于200。

2 吸附等温线的类型[8]

Ⅰ型等温线如图1所示。

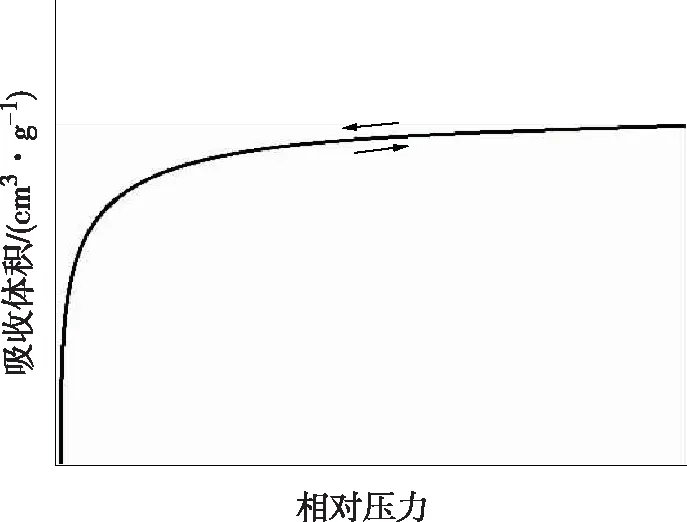
图1 Ⅰ型等温线

如图1所示，在较低的相对压力下吸附量迅速上升，达到一定相对压力后吸附出现饱和值，似于Langmuir型吸附等温线。一般Ⅰ型等温线往往反映的是微孔吸附剂(分子筛、微孔活性炭)上的微孔填充现象，饱和吸附值等于微孔的填充体积。

Ⅱ型等温线(图2)反映非孔性或者大孔吸附剂上典型的物理吸附过程，这是 BET公式最常说明的对象。由于吸附质于表面存在较强的相互作用，在较低的相对压力下吸附量迅速上升，曲线上凸。等温线拐点通常出现于单层吸附附近，随相对压力的继续增加，多层吸附逐步形成，达到饱和蒸气压时，吸附层无穷多，导致试验难以测定准确的极限平衡吸附值。

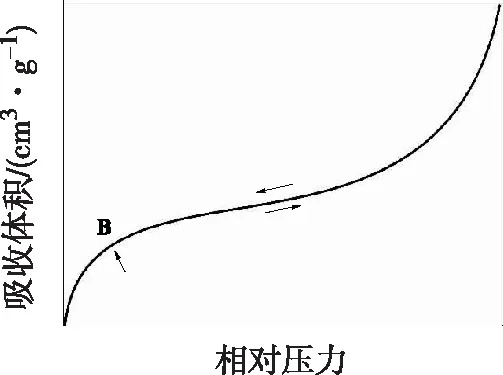
图2 Ⅱ型等温线

Ⅲ型等温线(图3)十分少见。等温线下凹，且没有拐点。吸附气体量随组分分压增加而上升。曲线下凹是因为吸附质分子间的相互作用比吸附质于吸附剂之间的强，第一层的吸附热比吸附质的液化热小，以致吸附初期吸附质较难于吸附，而随吸附过程的进行，吸附出现自加速现象，吸附层数也不受限制。BET公式中C值小于2时，可以描述为Ⅲ型等温线。

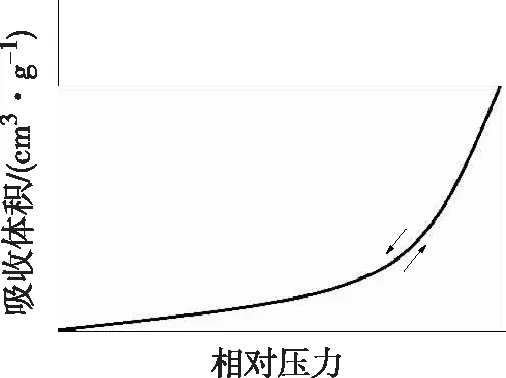
图3 Ⅲ型等温线

Ⅳ型等温线(图4)与Ⅱ型等温线类似，但曲线后一段再次凸起，且中间段可能出现吸附回滞环，其对应的是多孔吸附剂出现毛细凝聚的体系。在中等的相对压力，由于毛细凝聚的发生Ⅳ型等温线较Ⅱ型等温线上升得更快。

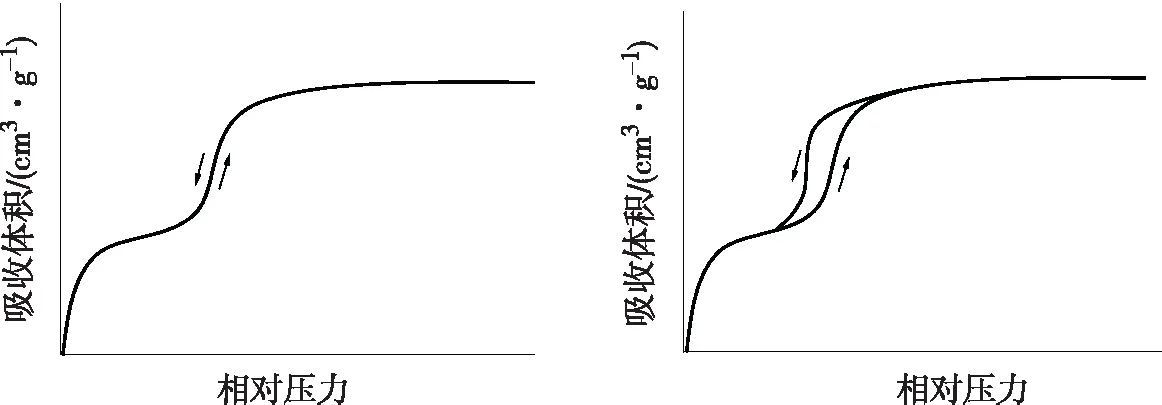
图4 Ⅳ型等温线

Ⅴ型等温线(图5)与Ⅲ型等温线类似，但达到饱和蒸气压时吸附层数有限，吸附量趋于一极限值。同时由于毛细凝聚地发生，在中等的相对压力等温线上升较快，并伴有回滞环。

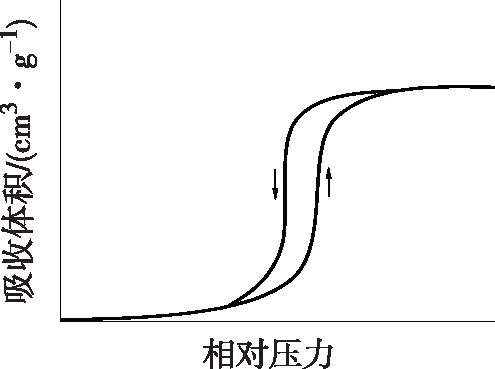
图5 Ⅴ型等温线

Ⅵ型等温线(图6)是一种特殊类型的等温线，反映的是无孔均匀固体表面多层吸附的结果(如洁净的金属或石墨表面)。实际固体表面大都是不均匀的，因此很难遇到这种情况。

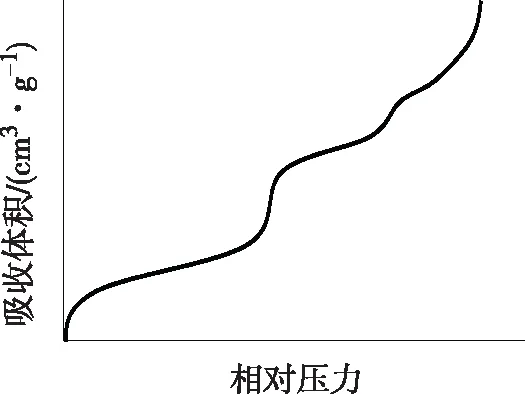
图6 Ⅵ型等温线

综上所述，由吸附等温线的类型反过来也可以定性地了解有关吸附剂表面性质、孔分布及吸附质与表面相互作用的基本信息，见表1。吸附等温线的低相对压力段的形状反映吸附质与于表面相互作用的强弱；中、高相对压力段反映固体表面有孔或无孔，以及孔径分布和孔体积大小等。

表1 吸附等温线反映的吸附质与表面相互作用和孔径分布信息

3 BET数据处理及分析

做完BET表征测试后，找出材料的比表面积、孔容、孔径，做出材料质构性质的表格。其中微孔体积是通过Dubinin-Radushkevich法计算得到，介孔体积是通过BJH法计算而得。

MOF-5和H6P2W18O62/MOF-5的质构性质见表2。平均孔径均约为3 nm，复合物H6P2W18O62/MOF-5的比表面积和孔体积明显比单一MOF-5增加，可推断出H6P2W18O62对MOF-5的结构有很大的影响，提高的金属有机骨架的孔体积和比表面积，以增强其吸附性能[9]。

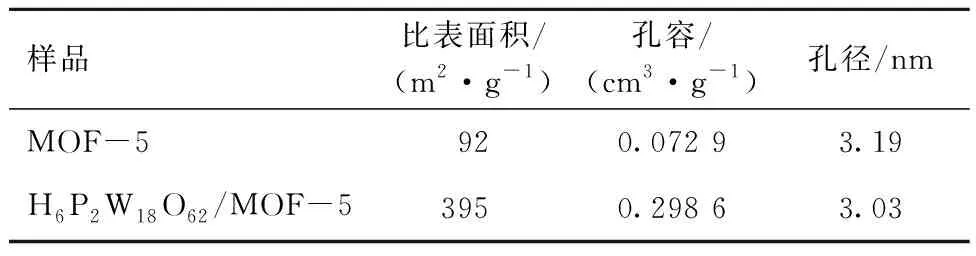
表2 MOF-5和H6P2W18O62/MOF-5的质构性质

H6P2W18O62/Cu3(BTC)2和Cu3(BTC)2的质构性质见表3。复合物H6P2W18O62/Cu3(BTC)2的比表面积和孔体积都增大，但孔径减少，表明H6P2W18O62的引入导致更小笼的形成[10]。

表3 Cu3(BTC)2 和H6P2W18O62/Cu3(BTC)2的质构性质

Zn(BDC)(Bipy)0.5和H6P2Mo18O62/Zn(BDC)(Bipy)0.5的质构性质见表4。它们的孔径分别为1.79 nm和1.92 nm，进一步证明两者均为微孔材料。Zn(BDC)(Bipy)0.5经过H6P2Mo18O62改性后形成的H6P2Mo18O62/Zn(BDC)(Bipy)0.5的比表面积和孔体积相对于纯骨架Zn(BDC)(Bipy)0.5减小了很多，进一步证实了H6P2Mo18O62负载在Zn(BDC)(Bipy)0.5骨架内或分散在Zn(BDC)(Bipy)0.5的孔道中。经H6P2Mo18O62修饰后，Zn(BDC)(Bipy)0.5内部的小孔相互作用，导致孔径增大，孔容减少，比表面积变小，增加了其吸附活性位点和驱动力。结合两者吸附性能的比较，进一步说明该复合物对MB的吸附受化学吸附控制[11]。

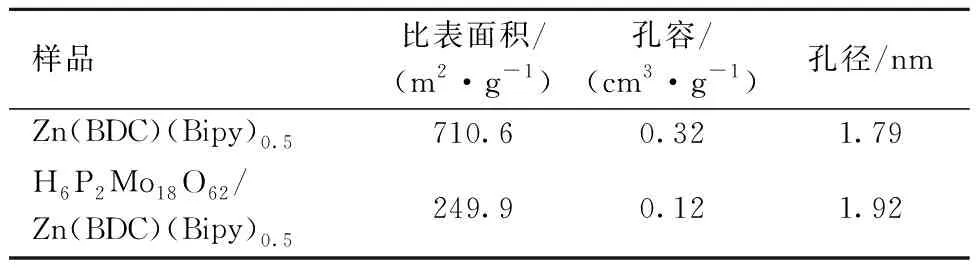
表4 Zn(BDC)(Bipy)0.5 和 H6P2Mo18O62/Zn(BDC)(Bipy)0.5的质构性质

不同H6P2W18O62负载量时H6P2W18O62/Cu3(BTC)2的质构性质见表5。随着H6P2W18O62负载量的增大，微孔体积和比表面积都增大，很可能因为H6P2W18O62与Cu3(BTC)2又构筑新的笼，导致结构变复杂，孔尺寸渐渐变小也说明此点。当H6P2W18O62含量为40%时，比表面积和微孔体积都减小，可能是杂多酸在骨架内部空腔或表面团聚[12]。

表5 不同负载量H6P2W18O62/Cu3(BTC)2的质构性质

Cu3(BTC)2和 H6P2W18O62/Cu3(BTC)2的N2吸附-脱附等温线和孔径尺寸分布分别见图7和图8。

2种材料在相对较低的压力下都有很高的N2吸附容量，且等温吸附线突然增大，均符合典型的Ⅰ型吸附等温线，表明微孔结构的存在，与孔尺寸分布一致，复合物的吸附容量增强，表明复合物有更多的孔，与表3所示比表面积和孔体积结果相符[10]。

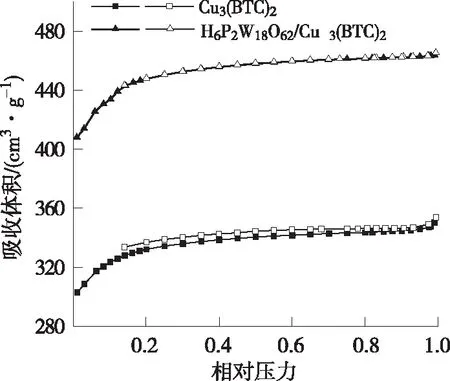
图7 Cu3(BTC)2 和H6P2W18O62/Cu3(BTC)2的N2吸附-脱附等温线

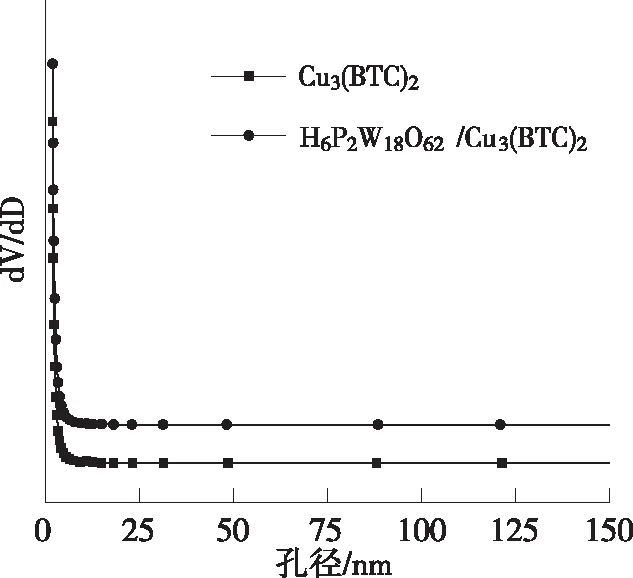
图8 Cu3(BTC)2 和H6P2W18O62/Cu3(BTC)2的孔径尺寸分布

4 BET计算中相对压力对材料比表面积的应用

考察在不同相对压力范围应用BET公式计算中孔材料、含少量微孔材料及纯微孔材料的表面积。

应用BET公式计算微孔材料的表面积时，多数微孔材料相对压力取值在0.05～0.20，计算出的表面积比相对压力取0.01～0.10时小。有少量的分子筛样品经水热老化处理后，其等温线产生低压滞后环,这类微孔材料在相对压力取值为0.05～0.20计算的表面积比相对压力取0.01～0.10时大。催化剂中微孔材料含量越多，两个相对压力范围内计算出的结果差别越大，对于纯分子筛样品二者差值可达15%左右。结果表明，在计算微孔材料表面积时，相对压力取值0.01～0.10，BET线性关系较为合理[11-12]。

中孔材料(氧化铝、氧化硅和氧化锆等[13-15])的测定中，中孔类材料的等温线基本为Ⅱ型或Ⅳ型等温线，其BET直线图中相对压力为0.05～0.20时，在Y轴上产生正截距。

裂化催化剂的等温线一般为Ⅰ型与Ⅱ型混合型等温线[16-18]，裂化催化剂在相对压力0.05～0.20的BET直线于Y轴产生负截距在此范围计算出的C常数没有物理意义。因此将BET线性范围缩小(向前推)，相对压力为0.01～0.10裂化剂的BET图在Y轴的截距基本上能转换为正值，而且直线线性关系好。因此，对于含微孔材料的裂化催化剂应用BET公式计算表面积时，相对压力取值0.01～0.10比0.05～0.20合理。

结果表明，用BET公式计算材料表面积时，微孔材料相对压力取值范围为0.01～0.1；中孔材料相对压力取值范围为0.05～0.2；裂化催化剂在相对压力0.01～0.10范围内计算合理。

5 展望

BET法测定材料的比表面积是一种很好的方法,在很多工业和科学研究行业中应用最广泛，测试结果最具可靠性。但是几十年来，人们对BET理论的修正和对BET公式的改进几乎没有停止过。对BET理论的修正包括：表面的不均匀性、吸附质分子间的横向相互作用、各层吸附热均有不同、吸附层数有限等。