尺寸约束下圆环阵MIMO声呐阵型设计和波束优化

伍镜蓉, 刘雄厚, 樊 宽, 孙 超, 杨益新



尺寸约束下圆环阵MIMO声呐阵型设计和波束优化

伍镜蓉, 刘雄厚, 樊 宽, 孙 超, 杨益新

(西北工业大学 航海学院, 陕西 西安, 710072)

传统主动声呐采用圆环阵接收可获得360° 视角, 但是在尺寸有限时面临着波束主瓣宽度大、旁瓣级高等不足, 针对这些不足, 文中提出了阵列尺寸约束下圆环阵多输入多输出(MIMO)声呐阵型设计和波束优化方法。圆环阵MIMO声呐由发射圆环阵和接收圆环阵组成, 通过优化发射圆环阵和接收圆环阵的半径和相对旋转角, 设计了具有低旁瓣波束的最优阵型。在该阵型的基础上, 通过将圆环阵MIMO声呐的波束优化问题转化为与其等效的虚拟平面阵波束优化问题(建立以旁瓣级最低为目标函数, 主瓣方向无失真响应, 并约束加权向量2-范数保证稳健性), 获得了期望的低旁瓣波束图。数值仿真结果表明, 所提方法可以在不增加阵列尺寸和波束宽度的前提下, 获得比传统圆环阵更低的旁瓣级。

MIMO声呐; 圆环阵; 虚拟平面阵; 阵型设计; 波束优化

0 引言

为了克服传统主动声呐的缺点, 多输入多输出(multiple-input multiple-output, MIMO)系统的工作模式得到广泛重视。不同于传统SIMO声呐, MIMO声呐利用独立发射波形和匹配滤波处理, 可以获得大量虚拟阵元并组成虚拟阵列, 在有限的物理尺寸下获得优于传统SIMO声呐的波束性能[5-6]。MIMO声呐虽然研究历史较短, 但是其研究现状丰富且不断发展, 国内外研究人员均获得了一系列研究成果。Bekkerman等[7]研究了密布式MIMO声呐的虚拟阵列和波束图, 证明其具有更高的角度估计精度和角度分辨率, 同时还推导了MIMO声呐用于目标检测的广义似然比以及用于目标方向估计的最大似然和克拉美罗界。Ma[8]通过使用不同中心频率的窄带信号研究了频率分集增益, 并在此基础上设计了最优接收滤波器。张友文等[9]研究了MIMO声呐自适应波束形成技术, 通过采用空间分集和波形分集的方法提高了MIMO声呐的探测性能。Wang等[10]提出了迭代法MIMO声呐目标检测, 有效提高了系统对弱目标的分辨能力。Liu等[11]讨论了MIMO阵列与其虚拟阵列之间的关系, 给出了虚拟阵元坐标的解析解, 并且提出了几种用于3D成像的MIMO声呐阵型; 同时还研究了单基地MIMO声呐的方位分辨率, 证明了MIMO声呐的有效孔径等于发射与接收联合孔径, 其方位分辨率由发射与接收阵列结构所决定[12]。

鉴于MIMO声呐相对于传统SIMO声呐的优势, 将其用在阵列尺寸受限的主动水声探测系统中具有一定的潜力和较好的应用前景。文中针对传统圆环阵SIMO声呐在尺寸有限时面临着波束主瓣宽度大、旁瓣级高的问题, 提出了尺寸约束下圆环阵MIMO声呐阵型设计和波束优化方法。该方法通过优化圆环阵MIMO声呐的发射与接收阵列, 设计了具有低旁瓣波束的圆环阵MIMO声呐阵型。以该阵型为基础, 将MIMO声呐的波束图优化问题转化为凸优化问题, 在一定的约束条件下利用CVX工具箱求解波束加权系数, 获得低旁瓣波束图, 达到了同时兼顾阵列尺寸、主瓣宽度和旁瓣级的目的[13-14]。

1 圆环阵MIMO声呐基本阵列结构

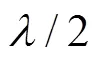
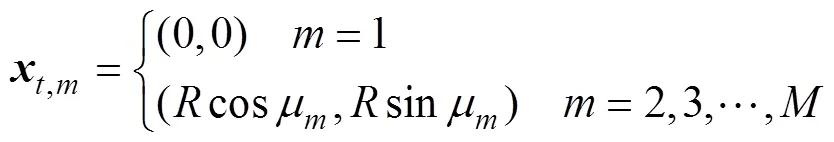
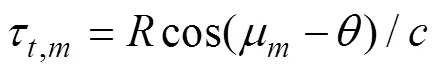
接收阵元的坐标向量

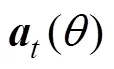
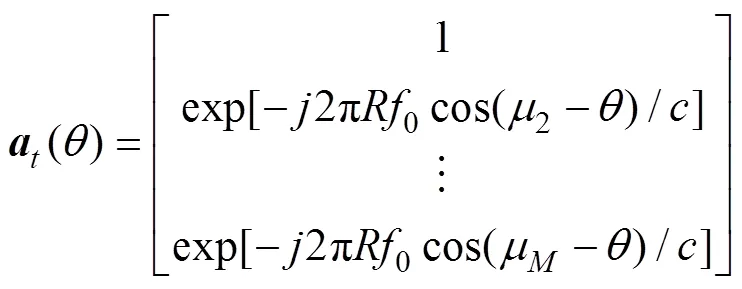
接收阵列流型向量[15]

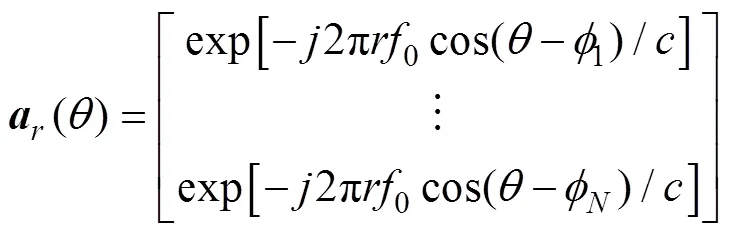
发射/接收联合阵列流型向量[12]

2 圆环阵MIMO声呐阵型设计与等旁 瓣波束优化

2.1 圆环阵MIMO声呐虚拟阵列

假设发收MIMO声呐的发射阵元同时发射相互独立的信号, 则每个接收阵元上的回波都可以看作是个独立波形的时域叠加。用个发射信号的拷贝对个回波信号进行匹配滤波处理, 获得个匹配滤波输出, 对应元虚拟阵元上的输出信号。此时, 该发收MIMO声呐可以等效为1发收SIMO声呐, 称这个1发收SIMO声呐是发收MIMO声呐的虚拟阵列, 其中虚拟阵列的阵元称为虚拟阵元。

远场条件下, 令1发收虚拟SIMO声呐的单个虚拟发射阵元位于坐标原点处, 则虚拟接收阵元的坐标向量等于1对实际的发收MIMO声呐的发射阵元坐标向量与接收阵元坐标向量之和, 即满足[16]

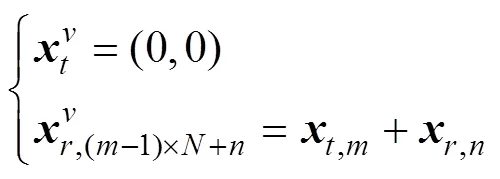
2.2 圆环阵MIMO声呐阵型优化

圆环阵MIMO声呐阵型优化基于常规波束形成(幅度加权为1的延迟求和波束形成), 其思路是: 在基本阵列结构下, 获得不同参数(对应图1中不同发射半径和相对旋转角)下不同主瓣指向的发射/接收联合波束图, 通过筛选最低平均旁瓣级(同一阵型不同主瓣指向下所有波束图旁瓣级的均值)所对应的阵列参数作为最优阵型参数,求解圆环阵MIMO声呐最优阵型。其流程图如图3所示。

2.3 低旁瓣波束优化

3 数值仿真与分析

3.1 最优阵型

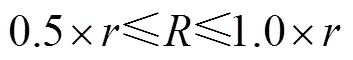
根据图4所筛选出来的最优阵型参数, 获得的5发16收圆环阵MIMO声呐最优阵型及其对应的虚拟阵列二维俯视图如图5所示。

3.2 低旁瓣约束下的波束图

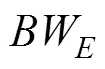
结合图6和表1可知, 当所期望的主瓣宽度为20°时, 5发16收圆环阵MIMO声呐和1发32收圆环阵SIMO声呐的旁瓣级均在-20 dB附近, 具有较强的干扰抑制能力。然而在波束性能相近的情况下, 比较2种圆环阵声呐的阵列尺寸可知, 5发16收圆环阵MIMO声呐的半径为1.09 m, 1发32收圆环阵SIMO声呐的半径为2.18 m, 前者半径为后者半径的一半。进一步比较5发16收圆环阵MIMO声呐和等尺寸1发16收圆环阵SIMO声呐的波束图可知, 5发16收圆环阵MIMO声呐的平均旁瓣级为–18.7 dB, 而1发16收圆环阵SIMO声呐的平均旁瓣级为–7.5dB, MIMO声呐的旁瓣级显著低于传统SIMO声呐的旁瓣级, 从而具有更优的干扰抑制能力。

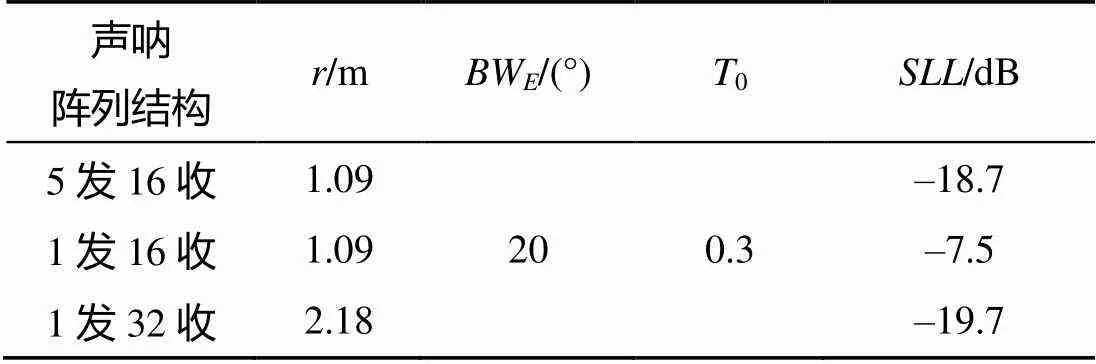
表1 不同阵列结构下的波束图参数

4 结束语

针对传统圆环阵SIMO声呐在尺寸有限时存在的波束主瓣宽度大、旁瓣级高的问题, 文中提出了尺寸约束下圆环阵MIMO声呐的阵型设计和波束优化方法。利用常规波束形成的方法设计了圆环阵MIMO声呐的最优阵型。在该最优阵型的基础上, 使用CVX工具箱对波束图旁瓣进行优化, 可知圆环阵MIMO声呐的波束性能与大尺寸圆环阵SIMO声呐的波束性能相似, 同时对比等尺寸下的圆环阵SIMO声呐的波束图可以发现, 圆环阵MIMO声呐具有更低的旁瓣级。

[1] Van Trees H L. Optimum Array Processing: Part 4 of Detection, Estimation and Modulation Theory[M]. Hoboken: John Wiley & Sons Inc, 2002.

[2] 孙超. 水下多传感器阵列信号处理[M]. 第1版. 西安: 西北工业大学出版社, 2007: 153-161.

[3] Davies D E. Circular Arrays: Handbook of Antenna Design, Vol.2[M]. IET Digital Library, 1983: 298-329.

[4] Ioannides P, Balanis C A. Uniform Circular Arrays for Smart Antennas[J]. Antennas & Propagation Magazine IEEE, 2004, 47(4): 192-206.

[5] Li J, Stoica P, Xu L Z, et al. On Parameter Identifiability of MIMO Radar[J]. IEEE Siganl Process Letters, 2007, 14(12): 968-971.

[6] Li J, Stoica P. MIMO Radar with Colocated Antennas[J]. IEEE Signal Process Magazine, 2007, 24(5): 106-114.

[7] Bekkerman I, Tabrikian J. Target Detection and Localization Using MIMO Radars and Sonars[J]. IEEE Transactions on Signal Processing, 2006, 54(10): 3873-3883.

[8] Ma N. Frequency Diversity for Active Sonar/Radar Application and Optimal Receiver Design[C]//Oceans 2010 MTS/IEEE Seattle. USA: IEEE, 2010.

[9] 张友文, 孙大军. MIMO声呐自适应波束形成技术研究[C]//2009年度全国物理声学会议会议录. 北京: 中国声学学会, 2009.

[10] Wang F P. An Iterative Way of MIMO Sonar Target Detection: A Method that Protrudes the Weak Target[J]. Applied Acoustics, 2010, 29(1):11-16.

[11] Liu X H, Chao S, Jie Z, et al. Devising MIMO Arrays for Underwater 3-D Short-Range Imagine[J]. Oceans, 2012, 11(18): 1-7.

[12] 刘雄厚, 孙超, 杨益新, 等. 单基地多输入多输出声呐的方位分辨力[J]. 声学学报, 2016, 41(2): 163-173. Liu Xiong-hou, Sun Chao, Yang Yi-xin, et aI. On Angle Resolution Mono-Static Multiple-Input Multiple-Output Sonar[J]. Acta Acustica, 2016, 41(2): 163-173.

[13] 鄢社锋, 马远良. 传感器阵列波束优化设计及应用[M].北京: 科学出版社, 2009: 112-118.

[14] 蒋光禹, 孙超, 刘雄厚, 等. MIMO声呐浮标低旁瓣波束优化[C]//2016年全国声学学术会议论文集. 北京: 中国声学学会, 2016.

[15] 杨益新. 声呐波束形成与波束域高分辨方位估计技术研究[D]. 西安: 西北工业大学, 2002: 14-15.

[16] 孙超, 刘雄厚. MIMO声呐概念与技术特点探讨[J]. 声学技术, 2012, 31(2): 117-124. Sun Chao, Liu Xiong-hou. MIMO Sonar: Concept and Technical Characteristic Discuss[J]. Technical Acoustics, 2012, 31(2): 117-124.

[17] 贺青, 罗来源, 姚山峰. 基于凸优化的小孔径圆阵波束形成研究与仿真[J]. 计算机仿真, 2016, 33(4): 15-18. He Qing, Luo Lai-yuan, Yao Shan-feng. Beamforming Design and Simulation for Small Aperture Circular Array Based on Convex Optimization[J]. Computer Simulation, 2016, 33(4): 15-18.

[18] 鄢社锋, 马远良, 孙超. 任意几何形状和阵元指向性的传感器阵列优化波束形成方法[J]. 声学学报, 2005, 30 (3): 264-270.Yan She-feng, Ma Yuan-liang, Sun Chao. Beampattern Optimization for Sonar Arrays of Arbitrary Geometry and Element Directivity[J]. Acta Acustica, 2005, 30(3): 264-270.

Array Layout Design and Beampattern Optimization for Circular-Array MIMO Sonar with Limited Physical Size

WU Jing-rong, LIU Xiong-hou, FAN Kuan, SUN Chao, YANG Yi-xin

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

By usinga receiving circular array, thetraditional active sonar can achieve a 360° view field. However, it suffers from a wide beamwidth and a high sidelobe level under the condition of limited physical size of the circular array. To address this problem, we focus on a circular-array multiple-input multiple-output(MIMO) sonar, and propose the corresponding array layout design and beampattern optimization method. The circular-array MIMO sonar is composed of a circular transmitting array and a circular receiving array. And for the purpose of suppressing the sidelobe level, the radius of the two arrays and the relative rotation angle between them are optimized synchronously. Furthermore, to obtain a low sidelobe beampattern, we calculate the weights on the virtual planar array of the designed circular-array MIMO sonar by solving a convex optimization problem. Specifically, the objective function is established to minimize the sidelobe level and set the mainlobe direction response without distortion, and the Euclid norm constraint on the calculated weights is used to ensure relatively robust beampattern performance. Numerical simulations show that the proposed method can obtain a lower sidelobe level than the traditional active sonar with same physical array size and same mainlobe width.

multiple-input multiple-output(MIMO) sonar; circular array; virtual planar array; array layout design; beampattern optimization

TJ630.34; TN929.3; TB566

A

2096-3920(2018)05-0415-06

10.11993/j.issn.2096-3920.2018.05.006

2018-07-25;

2018-09-18.

国家重点研发计划(2016YFC1400200); 国家自然科学基金(51509204); 西北工业大学中央高校基本科研业务费自由探索类项目(3102017ZY024).

伍镜蓉(1996-), 女, 在读硕士, 助研, 主要研究方向为水声信号处理。

伍镜蓉, 刘雄厚, 樊宽, 等. 尺寸约束下圆环阵MIMO声呐阵型设计和波束优化[J]. 水下无人系统学报, 2018, 26(5): 415-420.

(责任编辑: 陈 曦)