基于粒子群优化算法的目标运动参数估计

官善政, 陈韶华, 陈 川



基于粒子群优化算法的目标运动参数估计

官善政, 陈韶华, 陈 川

(中国船舶重工集团公司 第710研究所, 湖北 宜昌, 443003)

粒子群优化算法具有易于实现、可并行计算、收敛速度快且全局收敛等优点, 文中结合水下目标被动跟踪定位系统对目标运动参数估计的实时性和精确性需求, 提出了一种利用目标方位信息和多普勒频移信息估计目标运动参数的方法。该方法通过测量目标的方位角变化和多普勒频移, 基于最小均方误差(MMSE)准则建立参数估计方程, 并依靠粒子群优化(PSO)算法确定一组可使均方误差函数最小的运动参数, 实现对目标实时位置、航速、正横距离的精确估计。仿真结果表明, 与扩展卡尔曼滤波(EKF)算法对比, 在相同参数估计精度条件下, 粒子群优化算法能更快收敛; 对于小正横、高航速目标, 该算法能够在目标过正横前准确给出目标正横通过距离的预报, 并在目标过正横后提供较高的跟踪精度。文中工作可为水下目标被动跟踪和运动参数精确估计提供参考。

水下目标; 被动定位; 参数估计; 粒子群优化; 扩展卡尔曼滤波

0 引言

水下被动声基阵对目标实时位置的跟踪及相关运动参数的估计是水下目标被动探测的关键技术。目标运动分析(target motion analysis, TMA)法是一种常用的被动跟踪定位方法, 该方法通过测得的目标方位、时延、频率和相位等信息, 建立目标运动及观测模型, 实现对目标运动参数(目标位置、航速等)的估计[1]。

对于目标运动参数的求解, 刘健等[2]提出了一种带约束条件的最小二乘类方法, 解决了以往最小二乘估计算法(least squares estimate, LSE）在观测量和待估计量间呈非线性关系时有偏的问题。刘哲等[3]采用最大似然估计方法, 利用观测方程在当前运动参数估计值附近的泰勒级数展开, 得到该时刻目标运动参数估计值与观测值之间的伪线性关系, 实现了对目标运动状态的实时估计。刘圣松等[4]提出了一种以LSE估计结果作为迭代初值的卡尔曼滤波估计算法, 解决了迭代初值对参数估计性能影响较大的问题。以上方法中, 带约束条件的最小二乘类方法收敛速度较慢, 不能满足实时性需求; 最大似然估计方法对初值敏感, 且算法结构复杂; 卡尔曼滤波类方法计算简单, 通过对观测方程进行线性化能够良好应对弱的非线性问题, 但是无法应对目标状态量和观测量呈现强非线性关系的情形[5-6]。

对于水下目标而言, 目标的方位信息和线谱多普勒频移信息都是相对容易获取的观测量, 其同目标的航速和位置状态呈非线性关系。陈韶华等[7]利用基阵接收到的目标辐射噪声声强谱, 采用线谱的自动检测与提取方法检测线谱并估计线谱频率与方向, 得到目标从基阵附近经过时的观测序列, 并基于最小均方误差(minimum mean sq- uare error, MMSE)准则建立代价函数, 该代价函数的建立不需要观测量与目标状态量之间满足线性关系, 其中代价函数的自变量为目标起始位置和航速。使用粒子群优化算法求解一组可使代价函数最小的自变量, 可实现对目标实时位置、航速和正横距离的估计。

基于此, 文中提出一种利用目标方位信息和多普勒频移信息估计目标运动参数的方法, 并依靠粒子群优化算法求解有关参数, 以满足水下被动声基阵对目标实时位置的跟踪及相关运动参数精确估计的需求。

1 基本原理

1.1 定位原理

假设目标从观测点附近匀速直航通过, 以观测点为中心建立坐标系, 如图1所示。

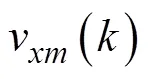
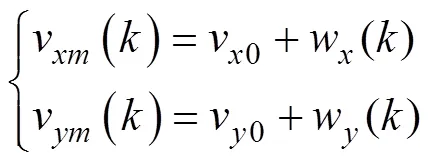
目标的位置

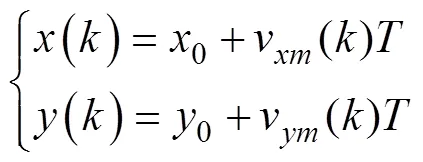
式中: (0,0)对应观测开始时目标所在的位置;为观测间隔。

观测点对目标方位和多普勒频率的测量结果

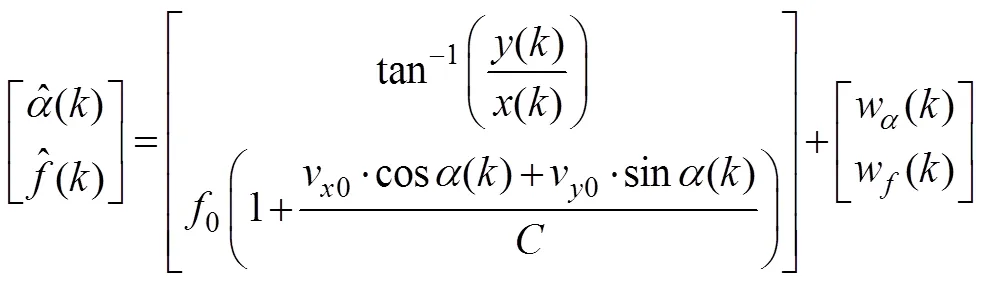
由式(1)~(3)基于MMSE准则构造代价函数(噪声误差函数)

其中

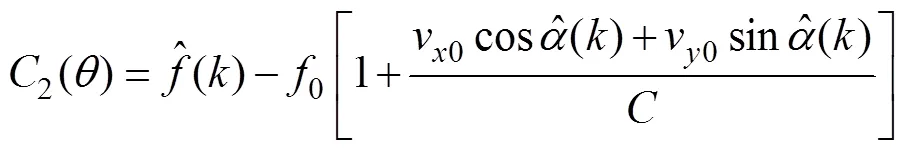
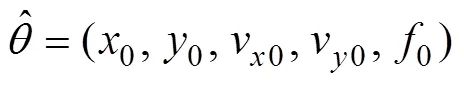
1.2 粒子群优化算法对目标运动参数的估计

对式(4)的求解实质上可以转化为一个最优化的问题, 可采用粒子群优化的方法来求解[8]。

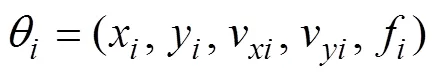
在求解过程中, 各粒子的坐标按照如下模式进行更新[9]

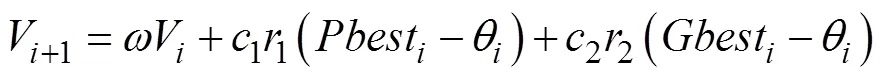
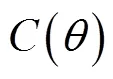
消去部分参数得

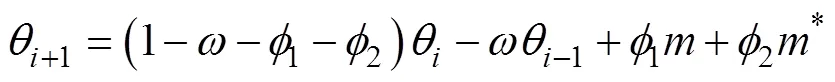
此迭代过程可以用矩阵表示为

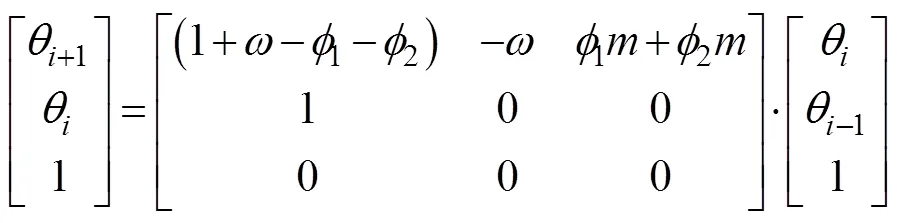
其中, 式(12)中矩阵的特征根容易求得为

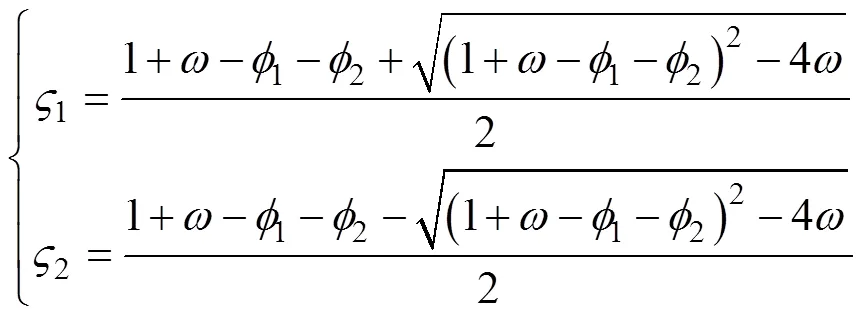
其中

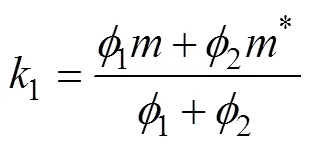
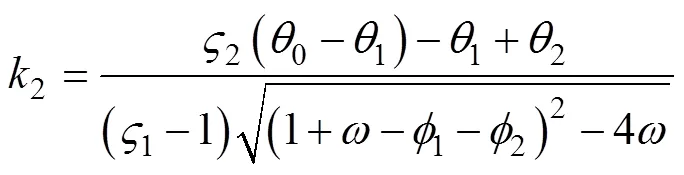
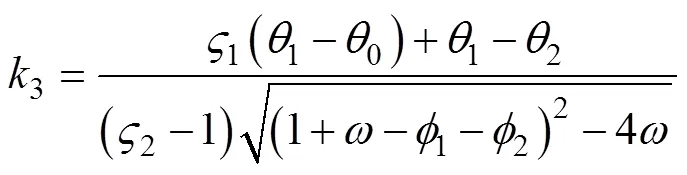
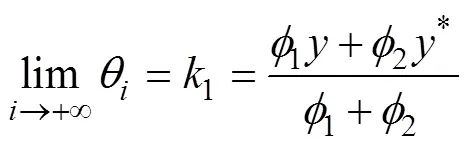
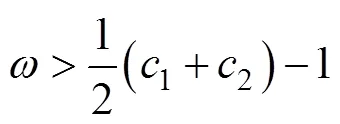
粒子群优化(particle swarm optimization, PSO)算法的求解步骤如下:

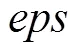
2 仿真分析

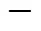
利用观测到的目标多普勒频率信息及方位信息, 使用PSO算法估计目标航迹和航速等参数, 并与利用相同观测量及观测方程的扩展Kalman滤波器所估计得到的参数进行对比。

设置种群规模与加速度常数为典型值, 采用PSO算法估计目标航迹和航速等参数, 并同扩展卡尔曼滤波(extended Kalman filter, EKF)估计的参数结果进行比对,如图6~图9。

从图6所示的PSO算法和EKF算法估计出的目标位置同目标真实位置的关系可看出, 这2种算法均可在一定观测时间后准确跟踪目标。

由图7~图9所示的目标运动速度估计、目标距离估计和目标正横通过距离估计的均方根误差曲线可知: 就航速估计而言, PSO算法在整个时间历程上是优于EKF算法的; 对于目标距离估计误差(跟踪误差), 若以误差稳定小于30 m作为收敛判定标准, 则PSO算法大约在15 s左右收敛, EKF算法则是在观测时间达20 s之后才收敛; 另外, 由图1对应的几何关系可知, 目标通过正横的时刻约为21.5 s, 在目标通过正横时, PSO算法给出的正横距离估计误差在4.21 m左右; 而EKF算法给出的正横距离估计误差在12.62 m左右。

3 结束语

针对常规目标运动参数求解方法存在跟踪精度不高、实时性低等不足, 文中结合目标被动跟踪定位在水下目标上的应用需求, 研究了一种依靠目标方位序列和多普勒频移序列构造代价函数(参数估计方程), 并利用PSO算法对目标运动参数进行解算的方法。数值分析表明, 相比较于EKF算法, 该算法具有较高的估计精度和更快的收敛速度。对于正横距离为30 m, 航速为25 m/s的高速目标, 算法能够在目标过正横前给出正横通过距离预报; 在目标通过正横后, 算法的距离跟踪误差在5 m以内。该方法可以满足水下被动声基阵对目标实时位置的跟踪及相关运动参数精确估计的需求。

在实际工程应用中, 由于部分目标航速较慢, 在远距离、大正横情况下的方位角变化和多普勒频移不明显, 尚需提升观测精度来减小参数估计误差。因此, 下一步研究工作将围绕提升观测量估计精度及优化算法收敛精度展开。

[1] 刘健, 姚海波．基于方位频率TMA的可观测性分析[J]．电光与控制, 2005, 12(6): 29-31.Liu Jian, Yao Hai-bo. Observability of TMA from Be- aring and Frequency Measurements[J]. Electronics Op- tics & Control, 2005, 12(6): 29-31.

[2] 刘健, 刘忠. 纯方位目标运动分析的无偏最小二乘估计算法研究[J]. 武汉理工大学学报(交通科学与工程版), 2010, 34(2): 262-265.Liu Jian, Liu Zhong. Study on Algorithm of Unbiased Least Square Estimator for Bearings-only Target Mot- ion Analysis[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2010, 34(2): 262-265.

[3] 刘哲, 卫军胡, 赵军, 等. 一种基于角度测量估计飞行目标运动参数的新方法[J]. 西安交通大学学报, 2008, 42(8): 986-990.Liu Zhe, Wei Jun-hu, Zhao Jun, et al. New Parameter Estimation Method for Flying Target Based on Bearing Measurements[J]. Journal of Xi’an Jiaotong University, 2008, 42(8): 986-990.

[4] 刘圣松, 陈韶华, 陈川. 一种水下静止平台对目标运动参数的联合估计方法[J]. 兵工学报, 2016, 37(4): 684- 689.Liu Sheng-song, Chen Shao-hua, Chen Chuan. Com- bined Algorithm for Motion Parameter Estimation of Target on Underwater Static Platform[J]. Acta Armamentarii, 2016, 37(4): 684-689.

[5] 陶林伟, 王英民. 基于扩展卡尔曼滤波的DIFAR浮标阵定位算法及分析[J]. 西北工业大学学报, 2011, 29(5): 738-744.Tao Lin-wei, Wang Ying-min. DIFAR(Direction Finding and Ranging) Sonobuoy Array Tracking Algorithm Based on Extended Kalman Filter(EKF)[J]. Journal of Northwestern Polytechnical University, 2011, 29(5): 738-744.

[6] 赵曦晶, 刘光斌, 汪立新, 等. 扩展容积卡尔曼滤波-卡尔曼滤波组合算法[J]. 红外与激光工程, 2014, 43(2): 647-653.Zhao Xi-jing, Liu Guang-bin, Wang Li-xin, et al. Aug- mented Cubature Kalman Filter/Kalman Filter Integr- ated Algorithm[J]. Infrared and Laser Engineering, 2014, 43(2): 647-653.

[7] 陈韶华, 陈川, 赵冬艳. 噪声中线谱的检测及自动提取研究[J]. 应用声学, 2009, 28(3): 220-225.Chen Shao-Hua, Chen Chuan, Zhao Dong-yan. Dete- ction and Automatic Cxtraction of Tonals Buried in Noise[J]. Applied Acoustics, 2009, 28(3): 220-225.

[8] Kennedy J, Eberhart R C. Particle Swarm Optimization [C]//Proceedings of the IEEE Conference on Neural Networks. Perth, Australia: IEEE, 1995: 1942-1948.

[9] 陈长忆, 叶永春. 基于粒子群算法的非线性方程组求解[J]. 计算机应用与软件, 2006, 23(5): 137-139.Chen Chang-yi, Ye Yong-chun. Solving Nonlinear Sys- tems of Equations Based on Particle Swarm Optimization[J]. Computer Applications and Software, 2006, 23(5): 137-139.

[10] 孙明杰, 陈月霞, 胡倩. 求解奇异非线性方程组的粒子群优化算法[J]. 黑龙江科技学院学报, 2006, 16(6): 369-373.Sun Ming-jie, Chen Yue-xia, Hu Qian. Particle Swarm Optimization Algorithm for Solving Singular Nonlinear Equations[J]. Journal of Heilongjiang Institute of Science and Technology, 2006, 16(6): 369-373.

Target Movement Parameter Estimation Based on Particle Swarm Optimization Algorithm

GUAN Shan-zheng, CHEN Shao-hua, CHEN Chuan

( The 710 Research Institute, China Shipbuilding Industry Corporation, Yichang 443003, China)

Considering the demand for real-time property and accuracy of an underwater target passive tracking and location system,a target parameter estimation method is proposed by using the target’s azimuth and Doppler shift information. With the measured target’s azimuth variation and Doppler frequency shift, a parameter estimation equation is established based on the minimum mean square error(MMSE) criterion, and a set of motion parameters is determined by the particle swarm optimization(PSO) algorithm to minimize the mean square error function, thus the accurate estimations of target’s real-time position, velocity, and closest passing distance are achieved. Simulation results show that the PSO algorithm converges more rapidly with equivalent convergence precision compared with the extended Kalman filter algorithm; and for the close-distance and high-speed target, the PSO algorithm can provide accurate prediction of target’s closest passing distance and high tracking precision before and after it passes by, respectively. This research is expected to provide a reference for passive tracking of underwater target and accurate estimation of movement parameters.

underwater target; passive location; parameter estimation; particle swarm optimization(PSO); extended Kalman filter(EKF)

TJ630.34; TN911.7; TB566

A

2096-3920(2018)05-0409-06

10.11993/j.issn.2096-3920.2018.05.005

2018-07-31;

2018-09-06.

国家重点研发计划(2016YFC1400200).

官善政(1993-), 男, 硕士, 研究方向为水下探测与控制技术.

官善政, 陈韶华, 陈川. 基于粒子群优化算法的目标运动参数估计[J]. 水下无人系统学报, 2018, 26(5): 409-414.

(责任编辑: 杨力军)