多假设跟踪中的高效匈牙利算法研究

赵伟康, 韩一娜, 张浩宇, 杨益新, 刘清宇



多假设跟踪中的高效匈牙利算法研究

赵伟康1, 韩一娜1, 张浩宇1, 杨益新1, 刘清宇2

(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 海军研究院, 北京, 100073)

作为多假设跟踪技术中的一项核心算法, 匈牙利算法占用了多假设跟踪中大部分的运算时间。考虑到多假设跟踪中的指派问题具有其特殊性, 即其效率矩阵是稀疏的, 文中提出了一种对效率矩阵进行降维的处理方法, 给出了运算流程, 对比了该方法与传统匈牙利算法在处理较大效率矩阵时的耗时, 结果表明, 在确保与传统匈牙利算法结果一致的前提下, 该方法能够大幅度降低运算量。

多假设跟踪; 匈牙利算法; 指派问题

0 引言

在理想假设条件下, 多假设跟踪(multiple hypothesis tracking, MHT)算法被认为是处理数据关联的最优方法[1]。区别于其他所有数据关联技术, MHT算法对所有可能的关联方案都维持一个假设, 并用一个树状结构来保存和管理这些假设, 该假设树随着扫描周期的推进进行横向和纵向的生长, 总体规模呈指数增长的趋势, 因此原始的MHT算法本质上是一种穷举寻优的方法。庞大的假设树为MHT算法带来了很大的运算量, 作为一种应用于工程实践中的算法, 需要抑制这种极快的问题规模增长, 目前成熟的MHT架构中包含了基于Murty算法[2]的-best策略以及-scan的枝剪策略[3], 前者用于控制假设树横向规模, 后者用来限制假设树深度。其中-best策略用以保留同一个假设下概率最大的个子假设而不是所有的子假设, 因此这就涉及到如何获得关联场景下概率最大分配的问题, 即MHT中的指派问题。匈牙利算法[4]目前在很多问题的求解中被应用[5-10], 也存在一些对匈牙利算法的改进策略。但MHT中的指派问题有其特殊性, 即其效率矩阵是稀疏的, 这提供了改进的空间。针对MHT中指派问题的特殊性, 文中提出了一种先将原效率矩阵降阶并运行匈牙利算法然后再还原成原效率矩阵对应解的方法, 在不破坏MHT架构的基础上可大幅度降低运算量。

1 指派问题与匈牙利算法

匈牙利算法最初由匈牙利数学家Edmonds于1965年提出, 用于解决二分图匹配问题, 后来该方法被推广应用到了带有权值的二分匹配问题, 即指派问题中。指派问题指的是在一个矩阵中寻找若干个不冲突的元素, 使得他们的和最大或最小, 在求最大值的问题中该矩阵称为效率矩阵。指派问题和匈牙利算法是运筹学中的经典案例。

图1表示效率矩阵是方阵以及非方阵时的指派问题, 可以看出, 当问题规模上升后, 指派问题的复杂度增长很快。

匈牙利算法的基本步骤如下[5]。

步骤1:获得指派问题的效率矩阵0(×);

步骤2: 首先从效率矩阵每行减去该行最小的元素, 再从每列减去该列最小的元素, 得到每行每列都至少有1个0元素的矩阵1;

步骤3: 寻找最少的直线覆盖1中的0元素得到2, 如果最少直线数等于, 转入步骤5, 否则转入步骤4;

步骤4:2中未被覆盖的元素减去这些元素中最小的元素, 同时在直线的交点加上该元素, 得到矩阵取代1转入步骤3;

步骤5: 从0元素最少的行或列开始指派, 直到各行各列都存在指派, 得到最优指派方案。

式中:表示效率矩阵;表示指派方案, 是与同阶的逻辑矩阵, 其中逻辑1表示矩阵中对应位置的元素被算法选中, 0表示没有选中;为方案对应的总效率。一般来说, 认为在对效率矩阵没有任何先验认识的条件下, 匈牙利算法是解决指派问题的精确且高效的方法。

2 MHT指派问题

MHT算法一般包含假设生成、假设组合和枝剪、假设管理等过程, 指派问题发生在假设的组合与枝剪过程, 此时MHT需要获取当前测量值所有关联情况的假设, 而将这些假设全部列举出来是不现实的。针对这一点, 指派问题的效率矩阵提供了一种直观表示所有假设的方法, 它依赖于MHT中的几条基本假设: 1) 同一个测量只能关联于当前的1个轨迹, 或成为杂波(虚警), 或成为新轨迹的起点; 2) 每个活动的轨迹在每个周期最多只关联于1个测量, 或被判断为漏报; 3) 所有杂波和新轨迹起点间没有关联性。

以上3个假设保证了MHT数据关联问题为指派问题, MHT中习惯使用后验的概率密度作为指派问题效率矩阵的关联效率, 因此, 一般MHT问题的效率矩阵具有如图2的形式[1]。

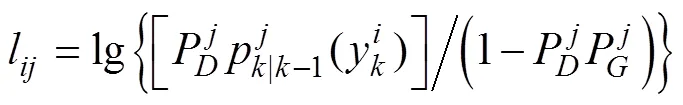
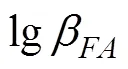
因此可以总结出, MHT的指派问题对应的效率矩阵是由1个完整矩阵和2个对角阵组成。另外考虑到MHT问题中每个周期的测量数量往往远大于活动的轨迹个数, 因此效率矩阵的第1个部分常常是1个行数大于列数的矩阵。

3 MHT指派问题改进方法

3.1 问题的数学化

将效率矩阵从MHT情景中剥离出来, 重新表示成如下更为普遍的形式:

图3中表示的矩阵最终是一个×(+2)的矩阵, 称为原始效率矩阵, 将矩阵划分成×的矩阵,阶对角阵和, 即=[,,]。显然将矩阵直接输入到式(1)表示的标准匈牙利算法可以获得最大效率和对应的指派方案, 但匈牙利算法在该类型的效率矩阵中产生了很多无意义的运算。主要原因是矩阵中大部分的信息集中在矩阵中, 而矩阵的规模常常远大于矩阵, 考虑到匈牙利算法较大的运算复杂度, 直接对矩阵运行匈牙利算法效率很低。

3.2 改进的方法

首先对该效率矩阵定义一个数列

因此该方法包含了如下的步骤:

步骤1: 获得原始效率矩阵;

步骤2: 将拆分成,,3个矩阵;

步骤3: 按照式(3)的规则获得矩阵;

4 性能分析与比较

4.1 理论分析

4.2 仿真与结果

表示一次扫描获得的量测数,表示huod2的轨迹数, 在最理想的跟踪环境下效率矩阵的每一列会存在一个值远大于其他值, 而且这些值不会出现在同一行, 此时匈牙利算法的意义并不明显。仿真时考虑最不理想的情况, 即量测中没有十分明显与轨迹关联的值, 矩阵,,中的元素为均匀分布的随机数, 由此组成的原始效率矩阵是对2个方法最不友好的。

为了更加直观地表示2种方法的运算量, 采用控制变量的思想, 在同一台计算机上用同样的编程语言使用2种方法解决同一个指派问题, 对比两者的运算时间。

由表1可见, 在和比较接近时, 改进方法效率提升了近1倍, 在明显小于时, 改进方法的优势更加明显, 能大幅下降输入匈牙利算法的矩阵规模, 效率上升了数十倍。

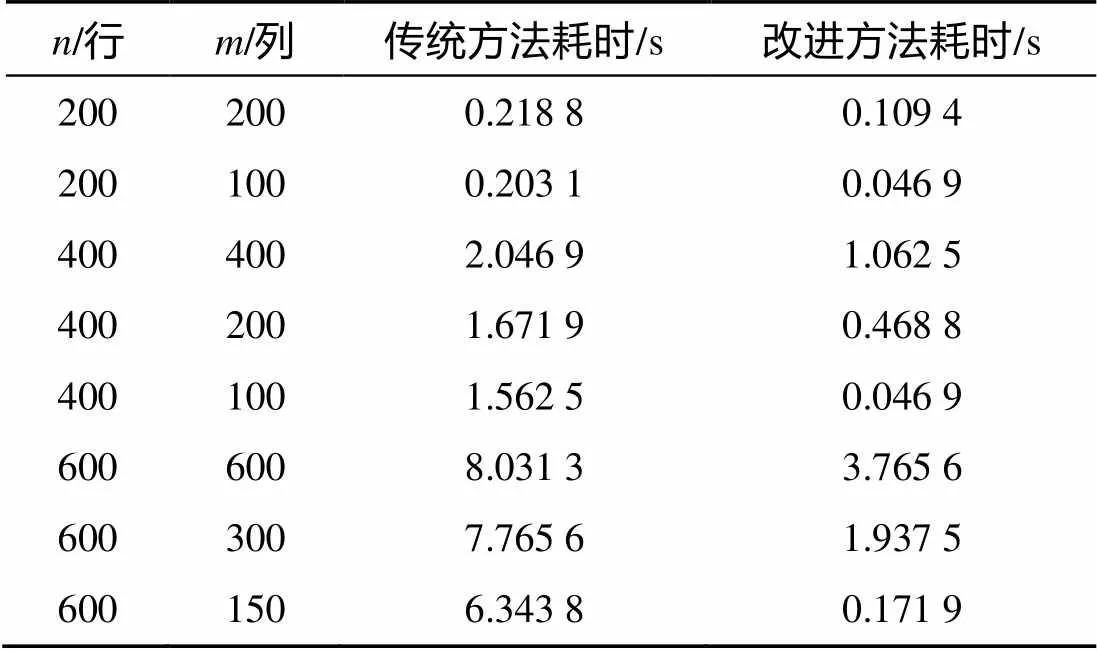
表1 不同规模问题的计算时间对比

5 结束语

文中提出了一种适合在MHT中使用的改进的匈牙利算法, 特点是运用在MHT中能保证获得与匈牙利算法完全一致的指派结果, 而运算复杂度较后者有很大的降低。该方法嵌入到MHT算法中表现稳定。

[1] 翟海涛. 多假设跟踪算法研究及其应用[J]. 信息化研究. 2010, 36(8): 25-27.Zhai Hai-tao. Reseach on Multiple Hypothesis Tracking Algorithm and Its Application[J]. Informatization Research, 2010, 36(8): 25-27.

[2] Murty K G. An Algorithm for Ranking All the Assignments in Order of Increasing of Cost[J]. Operations Research, 1968, 16: 682-687.

[3] Miller M L, Stone H S, Cox I J. Optimi­z­i­n­g Murty’s Ranked Assignment Method[J]. NEC Research Institute, Technical Report, 1997, 33(3): 851-862.

[4] 钱颂迪. 运筹学[M]. 北京: 清华大学出版社, 1998.

[5] Chin-Jung Huang. Integrate the Hungarian Method and Genetic Algorithm to Solve the Shortest Distance Problem[C]//2012 Third International Conference on Digital Manufacturi­ng & Automation. Guilin, China: IEEE, 2012: 496-499.

[6] Patel R R, Desai T T, Patel S J. Scheduling of Jobs based on Hungarian Method in Cloud Computing[C]//2017 International Conference on Inventive Communication and Computational Technologies(ICI­C­C­T). Coimbatore, India: IEEE, 2017: 6-9.

[7] Yan Chao-bo, Zhao Qian-chuan. Advances in Assignment Problem and Comparison of Algorithns[C]//27th Chinese Control Conference. Kunming, China: IEEE, 2008: 607-611.

[8] 张新辉. 任务多于人数的指派问题[J]. 运筹与管理. 1997, 6(3): 20-25.Zhang Xin-hui. Assignment Problem with Tasks More than the Number of Persons[J]. Operations Research and Manage- ment Science, 1997, 6(3): 20-25.

[9] 李延鹏, 钱彦岭, 李岳. 基于改进匈牙利算法的多技能人员调度方案[J]. 国防科技大学学报, 2016, 38(2): 144-149.Li Yan-peng, Qian Yan-ling, Li Yue. Multi-skilled Labor Allocating Method Based on Improved Hungary Algorithm[J]. Journal of National University of Defense Technology, 2016, 38(2): 144-149.

[10] 马晓娜.“人少任务多”型指派问题的一种新算法[J]. 重庆工商大学学报(自然科学版), 2014, 31(12): 68-75.Ma Xiao-na. A New Algorithm for Assignment Problems with “Tasks More Than the Number of Persons”[J]. Journal of Chongqing Technology and Business University: Natural Science Edition, 2014, 31(12): 68-75.

An Improved Hungarian Algorithm for Multiple Hypothesis Tracking

ZHAO Wei-kang1, HAN Yi-na1, ZHANG Hao-yu1, YANG Yi-xin1, LIU Qing-yu2

(1. School of Marine and Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2. Naval Research Academy, Beijing 100073, China)

Hungarian algorithm is a core algorithm in multiple hypothesis tracking technology, and it takes up most of the computation time in multiple hypothesis tracking(MHT). Considering that the assignment problem in the MHT has particularity, i.e., the efficiency matrix is sparse, this paper proposes a method for reducing the dimension of the efficiency matrix, and the computation flow is given. Comparison of the time consumption between the proposed method and traditional Hungarian algorithm in dealing with larger efficiency matrix shows that the proposed method greatly reduces the amount of computation while ensuring consistency with the results of the Hungarian algorithm.

multiple hypothesis tracking(MHT); Hungarian algorithm; assignment problem

TJ67; O224

A

2096-3920(2018)05-0444-05

10.11993/j.issn.2096-3920.2018.05.011

2016-11-19;

2016-12-18.

国家重点研发计划(2016YFC1400200); 国家自然科学基金面上项目(61671388).

赵伟康(1995-), 男, 在读硕士, 主要研究融合跟踪算法。

赵伟康, 韩一娜, 张浩宇, 等. 多假设跟踪中的高效匈牙利算法研究[J]. 水下无人系统学报, 2018, 26(5): 444-448.

(责任编辑: 陈 曦)