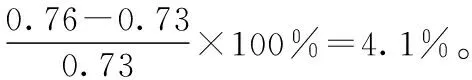车辆前照灯垂直自适应随动算法研究

黄新，丁志中

(1.芜湖技师学院，安徽芜湖 241000；2.合肥工业大学计算机与信息学院,安徽合肥 230009)

0 引言

文献[1]中指出，夜间发生交通事故的概率是白天的1.5倍，其中82%的事故都是源于缺乏充足的照明，所以自适应前照灯系统的研究对于提高交通安全有着重要的意义。相对于传统的前照灯，自适应前照灯系统能根据行驶路况和状态，由电子控制单元对车速、方向盘转角和前后轴高度信号进行分析处理，进而驱动步进电机不断对两侧大灯进行垂直和水平随动，以提供更合适的照明范围，确保驾驶员在任何时刻都拥有最佳的可见度。

目前自适应前照灯系统的研究在某些国家已经相对成熟，例如欧洲和日本已经实现了批量生产，并且针对自适应前照灯系统制定了相对完善的ECE R123[2]法规。而国内起步相对较晚，仍然处于自适应前照灯系统的探究与研发阶段。关于自适应前照灯系统的水平弯道算法，已见较多文献报道。然而对于自适应前照灯系统的垂直随动问题，研究报道并不多见。文献[3]中在研究车辆俯仰角的基础上,提出了建立垂直随动下的自适应最小均方滤波制动调光控制方法；文献[4]中对前照灯水平和垂直方向的偏转角度进行了简单的运动学建模；文献[5]中分析了自适应前照灯系统的垂直随动对改善高速路况照明的意义；文献[6]中分析了包括垂直随动的自适应前照灯系统的功能。然而这些文献没有涉及到自适应前照灯系统垂直随动的算法问题，而角度算法作为自适应前照灯系统的核心技术，对其研究关系着我国能否研发出具有自主知识产权的自适应前照灯系统。

文中通过建立车身姿态发生改变时对应的前照灯垂直随动的几何模型，结合四自由度半车振动模型和路面输入模型，提出了自适应前照灯系统垂直随动方面的角度算法，给出了角度算法对应的角度调整公式的详细推导，并对角度算法进行数值仿真实验分析其可行性，最后通过搭建简单的自适应前照灯系统的样机平台进一步验证了算法的有效性。

1 前照灯垂直随动的几何模型

路面状况或者车辆负载的改变，都会导致车身重心移动或者车身俯仰等状况的出现。这些状况会导致前照灯光束照射过远或者过近，从而影响照明效果[7]。

为了提高驾驶的安全性，需要在车身姿态发生改变的时候根据质心位移和车身俯仰角的变化对前照灯照射距离进行调整，从而使前照灯发出的光型既能够充分地照亮车辆前方的道路,又不会给对面来车驾驶员造成眩光,提高驾驶的安全性。

假设俯仰中心与车辆重心、车辆质心位于同一点，前照灯旋转轴线高度与车辆重心、车辆质心同高，同时考虑到车身发生俯仰运动及跳动时，前照灯照射距离必须满足车身姿态未改变时的照射距离，故车身发生前仰后俯时，对前照灯垂直随动的几何建模如图1所示；当车身发生前俯后仰时，对前照灯垂直随动的几何建模如图2所示。

图1 车身前仰时垂直随动的几何模型

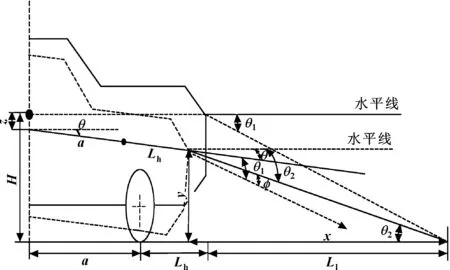
图2 车身前俯时垂直随动的几何模型

由图1中的三角函数关系可得：

(1)

其中：y=H+z+(a+Lh)sinθ；x=Ll+[(a+Lh)-(a+Lh)cosθ]。

分析图1中的几何关系有：

φ=θ-(θ1-θ2)

(2)

根据公式(1)和(2)可得到：

(3)

式中：a为质心到前轴的距离；H为车灯安装高；Lh为前轴到前照灯的水平距离；θ1为正常情况下前照灯的初始照射角度；Ll为车身姿态未改变时的前照灯初始照射距离；θ2为车灯修正后与水平方向所成的角度；φ为车灯调整的角度；θ为车身俯仰角；z为车身质心垂直位移。

与图1分析类似，由图2有：

(4)

φ=θ+(θ1-θ2)

(5)

式(4)与式(1)不同的是，其中：y=H-z-(a+Lh)sinθ，x=Ll+[(a+Lh)-(a+Lh)cosθ]。

结合式(4)和式(5)，当运动中车身发生前俯后仰时，对前照灯的调整角度如下：

(6)

其中：ECE R123中规定车灯安装高度H为0.68 m；另外式(3)和式(6)中车灯的初始照射角度为θ1，由文献[8]可知为0.6°，同时为了满足车辆行驶安全性，初始照射距离至少应该达到安全制动距离，即Ll=s(v)，其中安全制动距离s(v)与车速v的关系如下：

s(v)=0.009 4v2+0.605 7v+3.173 0[9]

(7)

2 车身俯仰角与质心位移的计算模型

通过对前照灯系统垂直随动几何模型的分析，可知前照灯的调整角度与车身俯仰角、质心位移有关。考虑到全车模型结构过于复杂，不易实现，四分之一车辆模型过于简单，不能表征车身俯仰角和质心位移，下面基于四自由度的半车振动模型建立车身俯仰角与质心位移的计算模型[10]。

如图3所示，这4个自由度分别是质心垂直位移z、俯仰角θ、前轴垂直位移z1和后轴垂直位移z3。图中mhb是半车质量，mf、mr分别是前、后轮的质量，Ff、Fr分别是前、后悬架力，a、b分别是质心到前、后轴的距离，z2、z4分别是以点1、2为原点的位移，z0是地面的垂直位移，由车辆前、后轴高度传感器分别得到H1(t)=z2(t)-z1(t)，H2(t)=z4(t)-z3(t)。

图3 四自由度半车振动模型

由牛顿第二定律和转动定律建立动力学方程，求解质心位移和车身俯仰角如下：

(8)

(9)

其中俯仰角较小时，以点1、2为原点的位移z2、z4与质心位移z有如下近似关系[11]：

另外：

(10)

(11)

式中：ksf、ksr分别是前、后悬架的弹性系数；csf、csr分别是前、后悬架的阻尼系数；ktf、ktr分别是前、后轮的弹性系数。

粗糙度不同的路面，地面垂向位移也不同，z0(t)可用时域路面输入模型来描述，为了更真实地反映路面谱在低频范围内近似为水平的实际情况，在路面谱模型中引入一个下截止频率f0[12]。

(12)

式中：G0为路面不平度系数；w(t)为均值是零的高斯白噪声。

车辆以不同的速度行驶在粗糙度不同的路面上，车身质心位移和车身俯仰角度也会相应发生变化。利用路面输入模型模拟真实的路面，然后基于四自由度半车振动模型求解车身质心位移和车身俯仰角，进而可以利用相应的几何模型得到车灯的调整角度。

3 仿真结果分析

颠簸路面以及车辆负载导致车身姿态发生改变时，由车速传感器和前后轴高度传感器得到车速和前后轴高度信号。首先根据前后轴高度信号判断车身的俯仰情况，若车身发生前仰后俯时由公式(3)计算出前照灯在垂直方向对应的调整角度，若车身发生前俯后仰时由公式(6)计算出前照灯在垂直方向的调整角度，最后通过反向调整前照灯的照射角度以达到最佳照明。

下面对自适应前照灯系统的垂直调光算法进行仿真实验，首先用滤波白噪声积分法生成随机路面，然后用Simulink对公式(8)—(12)进行建模求解，得到车身俯仰角和质心位移，再分别根据公式(3)和(6)对调整角度进行仿真实验，求解过程中涉及到的参数见表1[3]。

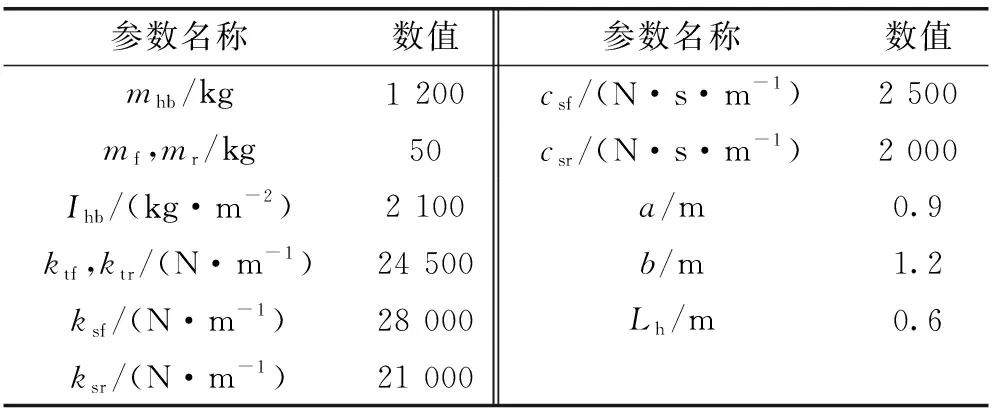
表1 半车模型参数

为了保证时域路面输入位移与实际谱一致，下截止频率f0取0.062 8 Hz。另外在路面等级中C级表示路面基本没有坑洞，D级以下代表的是粗糙的路面，由于车身姿态改变引起的垂直随动主要是针对崎岖路面，故G0分别取C、D、E级路面振动对应的功率谱密度256×10-6、1 024×10-6、4 096×10-6m-1进行仿真。

路面级数不同，车身前后轴高度传感器采集的数值就不同，此时设车辆行驶速度v=20 km/h，图4、图5分别是在C、D、E级路面下仿真出的前照灯垂直向下和向上的调整角度。

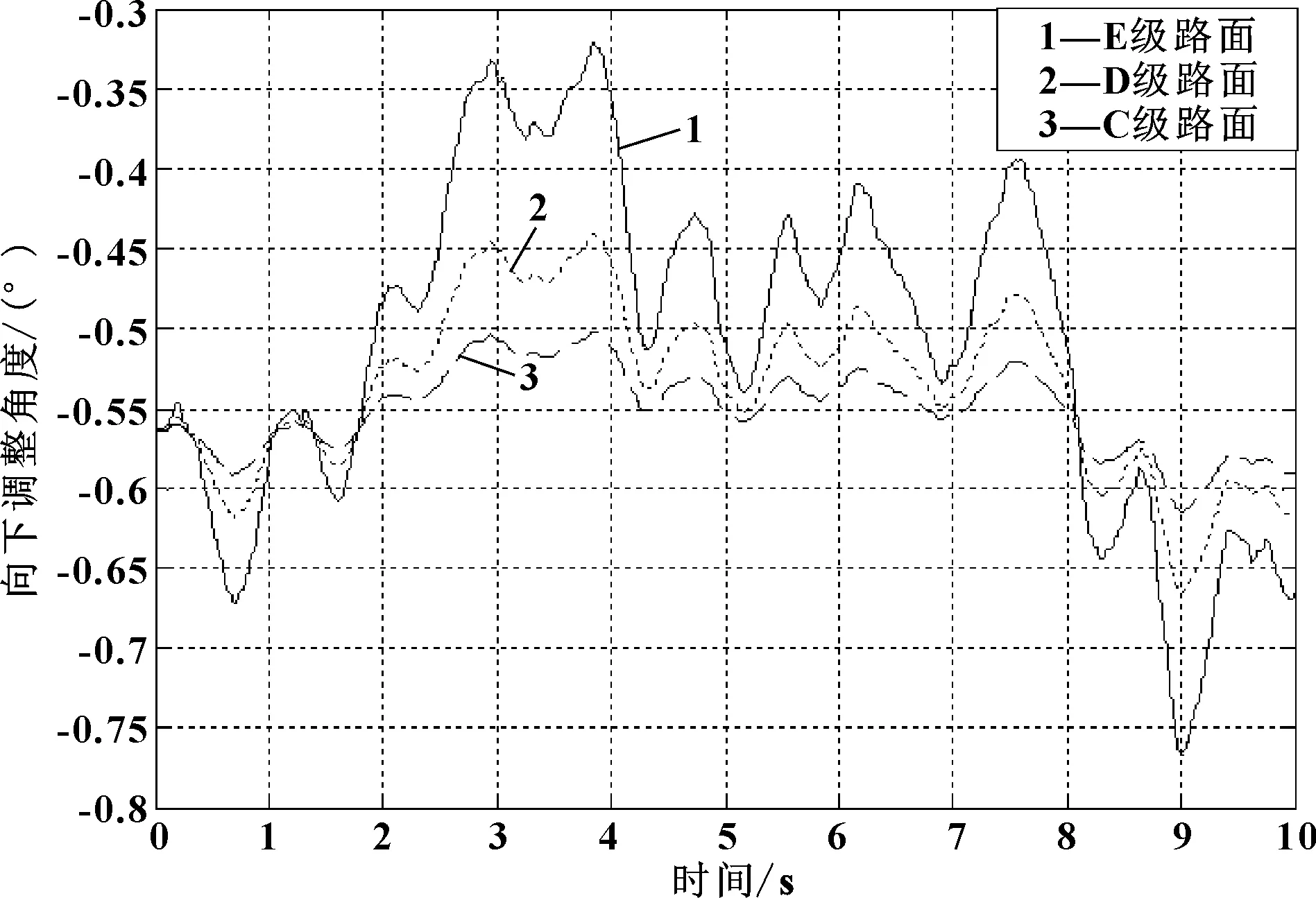
图4 不同路面对应的向下调整角度

图5 不同路面对应的向上调整角度

图4是车辆在行驶过程中当车身发生前仰后俯时，根据公式(3)计算出来的前照灯调整角度的仿真曲线，可以看出调整角度为负数，即需要向下调整对应的角度，且路面级数越高调整幅度越大，对于相对平坦的C级路面，调整角度在0.55°左右小幅波动，对于比较粗糙的E级路面，对应的调整角度在0.32°～0.76°之间有相对较大幅度的波动；图5则是当车身发生前俯后仰时，根据公式(6)计算出来的前照灯调整角度的仿真曲线，同样路面级数越高所需调整幅度越大，对于E级路面前照灯最大调整角度为0.73°。

前照灯垂直调整角度与前后轴高度、车速有关。前后轴高度可以通过设置不同的路面级数反映出来，以上分析了在不同路面级数以同一车速运动时前照灯的垂直调整角度。现在G0取E级路面振动的功率谱密度4 096×10-6m-1，分析车辆分别以速度v=20、40、60 km/h行驶时，对应的前照灯垂直向下和向上的调整角度分别如图6和图7所示。

图6 不同车速对应的向下调整角度

图7 不同车速对应的向上调整角度

图6是车辆以不同速度行驶时，根据公式(3)计算出来的前照灯调整角度的仿真曲线。图7是根据公式(6)计算出来的前照灯调整角度的仿真曲线。其中调整角度为负时，代表前照灯需要向下调整对应的角度。车速越大时，调整角度对前照灯照明的影响越大，故车速较大时调整幅度不易过大。由图6和图7可以看出，车速越大时，前照灯调整幅度相应变小，符合驾驶安全性的规律。同时前照灯向下调整的角度最大为0.76°，向上调整的角度最大为0.73°。

以上基于MATLAB/Simulink的仿真实验证明了垂直调光算法的合理性，进一步在实验室搭建一个简单的AFS系统样机实验平台，在样机平台上对自适应前照灯系统的垂直调光算法进行验证，实验平台如图8所示。

图8 自适应前照灯系统样机平台

该系统的前照灯采用的是上海大众斯柯达昊锐SK-98760型前照灯，核心控制部分采用台湾民生单片机CS8959芯片，前后轴高度传感器信号和车速信号分别采用电位器和波形发生器进行模拟，通过设置不同的前后轴高度值和车速值查看车灯的调整角度。车灯调整角度主要通过覆盖在车灯上的量角器测得，经测试角度旋转范围为-1°～1°，跟仿真角度基本吻合。

4 结束语