序列相关性在资产组合绩效改善中的作用
李 斌,张 迪,冯佳捷
武汉大学 经济与管理学院,武汉 430072
引言
随着中国社会财富的持续积累,理财观念日益深入人心,如何科学地管理资产成为一个亟待解决的现实问题。许多研究围绕该问题展开,如尹力博等[1]、徐佳等[2]、吴卫星等[3]和陈永伟等[4]的研究。均值-方差理论[5]首次将数量方法引入资产组合中,奠定了现代金融研究的基础。然而均值-方差(mean-variance,MV)最优风险组合的样本外绩效表现不及预期,甚至不如简单的等权重(equal weighted, EW)组合,即简单分散化组合[6]。这是因为最优风险组合依赖于资产的期望收益和真实方差,而提前获得这些信息是困难的[7],实践中往往采用历史样本的样本均值和方差测量期望收益和真实方差。真实值与估计值之间的估计误差是造成最优风险组合样本外绩效较差的主要原因,因此减少估计误差是改善资产组合绩效的重要研究方向。估计误差主要来源于期望收益和协方差矩阵的估计过程[8]。中国股票市场的证据表明[9],等权重组合在中国A股市场上获得了较好的收益,超过了均值-方差组合及其拓展组合等其他组合。可能的原因是样本均值的估计误差较大,从而造成均值-方差组合的表现不佳。资产收益的序列相关性在证券市场中广泛存在,投资者往往可以从资产价格的序列相关性中获得对未来收益的更好预测,从而获得超额收益,如动量效应[10]、反转效应[11]和趋势策略[12]。因此,本研究利用资产收益的序列相关性改进对期望收益的估计,并结合收缩估计方法提高资产组合的样本外绩效。
1相关研究评述
已有研究中改进组合样本外绩效的思路包括贝叶斯方法[13]、稳健贝叶斯方法[14]、利用稳健投资者[15]和稳健估计值[16]的非贝叶斯方法以及利用包括特定资产特征[17]、股票横截面特征[18]和期权特征[19]等边际信息的方法。其中,利用边际信息的方法通过利用历史收益信息以外的其他信息来增加组合收益[20],而贝叶斯方法和非贝叶斯方法根据历史收益信息提出期望收益和风险的更优估计值,减少估计误差。已有的改进方法按照改进对象分为3类,第1类方法改善期望收益的估计误差,第2类方法改善协方差矩阵的估计误差,第3类方法直接改善组合权重误差。PSTOR et al.[21]发现在较长的估计窗口下,贝叶斯方法提高绩效的效果并不明显;DEMIGUEL et al.[22]利用期权市场数据和无模型隐含波动率方法提取期权信息,发现期权隐含波动率的风险溢价和偏度有助于提高组合的样本外夏普比率;DEMIGUEL et al.[16]将稳健估计的思想应用到组合选择领域,改进了稳健M估计值和稳健S估计值。
忽略期望收益的估计只考虑协方差矩阵也是一种可行的办法。最小方差组合不依赖于资产的期望收益,可以减少估计误差,因此受到学者的广泛关注[23]。对于协方差矩阵的估计误差,LEDOIT et al.[24]提出一种收缩估计方法,在结构化矩阵和历史数据估计矩阵中取得一种良好的权衡取舍。收缩估计思想也被用于改进协方差矩阵,收缩对象可以是协方差矩阵[25]及其逆矩阵[26],估计方法包括主成分分析方法和谱估计方法等[27]。另外,范数约束还将贝叶斯方法和矩估计方法考虑到组合的优化过程中。基于期权信息[19,22]、因子模型[28]、稳健估计[16]和换用高频数据[29]都可以对协方差矩阵估计进行改进。
为了降低参数不确定性带来的影响,收缩估计方法被应用于资产组合权重的直接优化过程。JORION[30]提出Beyasian-Stein规则,对参数不确定性做了初步探索,并提出一种基于组合联合思想的新框架。随后的研究者在此基础上,通过变换收缩的对象和目标函数,提出一系列的新组合。KAN et al.[31]利用收缩估计的思想,通过最大化效用函数,提出在最小方差组合、简单分散化组合和无风险资产之间配置资产的三基金模型;DEMIGUEL et al.[32]通过施加范数约束,提出一个新的投资组合选择模型。本质上,施加范数约束属于广义的收缩估计。TU et al.[33]将等权重组合和其他改进策略进行联合,投资组合的绩效得到改善。另外,卖空约束在理论和实践中都被证明有助于减少估计误差。
本研究与资产收益序列相关性也有一定的联系。关于股票收益序列相关的研究可以追溯到LO et al.[11]的研究,他们发现反转策略在美国股票市场上可以获得超额收益;JEGADEESH et al.[10]提出动量策略收益来源分解范式,认为资产收益相关性是动量策略收益的来源;DEMIGUEL et al.[34]从股票收益的序列相关性出发,利用向量自回归(vector auto-regression,VAR)模型改善投资组合的样本外绩效。虽然向量自回归模型能够减少期望收益的估计误差,但是换手率较高,在个股组合上的表现也不尽理想。
中国学者在资产配置方面也进行了一系列的研究。李爱忠等[35]通过集成预测方法改善均值-方差组合的绩效,说明采用更加精确的预测方法能够改善均值-方差组合的绩效;黄琼等[8]检验基于均值-方差理论的各种改进组合在中国市场上是否适用,结果发现等权重组合比最小方差组合、均值-方差组合及各种拓展组合的样本外绩效更好;韩其恒等[9]用中国资本市场数据和仿真数据对资产配置模型的适用性进行全面检验,并给出切实可靠的政策建议。这些研究结果肯定了估计误差在资产组合配置过程中的重要影响。姜富伟等[36]通过对A股股票分组,发现简单的移动平均策略也能够获得显著超额收益。这说明A股市场存在显著的序列相关性,也提供了序列相关性适用于资产配置领域的证据。尹力博等[37]将宏观经济因素纳入VAR模型,从定性的角度提出跨资产类的配置建议,肯定了VAR模型在指导资产组合配置领域的价值。
中国学者对股票市场序列相关性进行了详细的研究,但是将序列相关性用于改进资产组合绩效的相关研究并不多[38]。对均值-方差理论有效性的研究更倾向于对比不同的成熟策略,验证这些策略在中国市场上的有效性、改进投资组合绩效的相关实证研究还比较缺乏。针对以上问题,本研究将序列相关性纳入对期望收益的估计,用VAR模型预测值代替样本均值测量期望收益,并利用施加约束和收缩技术等各种改进措施提高组合的绩效,选取中国A股市场数据进行实证分析,通过对比14种资产组合的样本外绩效和最优收缩强度的分布,找到支持均值-方差理论有效性的证据。
2理论模型和组合构建
2.1问题设定
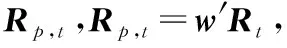
实践中,真实的μ和Σ未知,估计误差的存在导致估计的w*有偏。因此,许多研究提出了改进w*估计的方法,包括只估计协方差矩阵的最小方差组合、空头约束、范数约束和勒杜瓦-沃尔夫(Ledoit-Wolf, LW)收缩协方差矩阵[24]等。
2.2利用序列相关性改善期望收益估计值
期望收益和风险的估计值决定了最优风险组合。在滚动估计窗口下,均值-方差模型输入值的频繁变动会引起组合权重的较大波动,因此样本外绩效较差。由于协方差矩阵有相对精确的测量,只关注风险的最小方差组合不受期望收益估计误差的影响,因此得到更多的关注[39]。李金鑫等[40]的实证结果表明,只考虑协方差矩阵的最小方差组合能够改善均值-方差组合的样本外绩效。这与BEHR et al.[41]的结论一致。DEMIGUEL et al.[16]的研究证明,估计期望收益过程中产生的误差约是估计协方差矩阵过程中的9倍。因此,与协方差矩阵相比,改善期望收益的估计误差理论上能够更大程度地改善投资组合绩效。
改善期望收益的估计误差有3种思路。①估计值的一致性表明增加估计区间长度可以改善期望收益的估计误差。DEMIGUEL et al.[6]的研究表明,在25种资产情形下,如果使新估计区间下最优风险组合的夏普比率超过等权重组合,至少需要3 000期的估计窗口长度;在50种资产的情形下,则需要6 000期的估计窗口长度。因此这种方法不具有实用性。②贝叶斯方法通过调整期望收益估计值与真实值间的差异来减少估计误差。但是这类方法证明难度较大,依赖于对收益分布的假设,因此效果并不明显[21]。③资产收益的序列相关性也是一种可能的研究方向。股票收益之间存在序列相关性,包括代表自相关性的动量效应和反转效应,以及横截面相关性的市值效应和账面市值比效应。这些股票市场异象能够带给投资者显著的收益,表明历史收益对未来收益具有一定的预测能力[42],因此本研究将序列相关性应用于改善期望收益的估计。
考虑到非线性关系的复杂性,本研究考虑线性相关关系,VAR模型和自回归滑动平均模型(autoregressive moving average model, ARMA)是常见的时间序列线性模型,ARMA模型只考虑收益序列的自相关关系,而VAR模型同时刻画自相关关系和横截面相关关系。因此,本研究将VAR模型引入期望收益的估计中,以VAR模型的预测值代替样本均值作为期望收益的估计值。需要说明的是,预测股票收益是很难的,几乎没有一个好的模型能预测股票收益。虽然VAR模型可能并不是一个好的股票收益预测模型,但是如果VAR模型预测值是一个比样本均值更好的期望收益估计值,那么均值-方差最优风险组合的绩效就能够得到改善。因此,本研究的第1个研究目的是对比不同约束条件下均值-方差组合与VAR模型下的均值改善组合,验证序列相关性是否能够改善投资组合的样本外绩效。
在建立VAR模型的过程中,滞后阶数p根据信息准则确定,N个变量(即N种风险资产)的VAR模型待估参数为(N2p+N)。而股票的收益序列长度与采用的数据频率有关,因此需要在模型预测精度与现实样本长度之间进行权衡取舍。由于本研究采用月度数据进行实证,样本长度较为有限,因此使用待估参数最少的一阶VAR模型来描述股票收益的序列相关性,即
Rt+1=α+βRt+εt+1
(1)
其中,Rt为第t期的超额收益向量,Rt∈N,N为N维实数向量;α为对应的截距项,α∈N;β为斜率矩阵,β∈N×N,N×N为N×N维实数向量矩阵;εt+1为误差项,服从正态分布的独立同分布变量,假定其协方差矩阵为正定矩阵。VAR模型假定(t+1)期每只股票收益线性依赖于t期股票收益。β刻画了这种线性关系,其元素βi,j为i股票第t期收益对于j股票第(t+1)期收益的边际影响,i和j分别表示两种不同的资产。因此,VAR模型可以刻画资产间的线性关系,包括自相关关系和横截面相关关系。为了减弱多重共线性问题,(1)式采用岭回归逐一对模型参数进行估计。
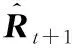
2.3收缩估计组合
首先,使用VAR模型预测值代替样本均值对最优风险组合有双重影响。①与样本均值相比,VAR模型的预测值更加准确,组合权重更接近于真实最优组合,能够改善组合的样本外绩效;②VAR模型预测值的波动性可能比均值的波动性更大,组合权重的波动也更大,从而可能产生较高的交易成本。因此,VAR模型预测值对投资组合绩效的影响并不明确。其次,虽然施加范数约束能够在一定程度上减弱预测值波动带来的影响,但是对美国日度股票收益的实证结果表明,VAR模型对应的改善组合换手率较高[34]。具体表现为,在5~10个基点的交易成本下,VAR模型对最优风险组合样本外夏普比率的改善能力消失[34]。这说明,只有在低于5个基点的交易成本下该方法才有效。针对均值改善组合换手率高的特点,本研究利用收缩估计技术将均值改善组合与等权重组合联合起来,并从理论和实证上说明收缩估计组合在绩效表现上是否更加稳健,这是本研究的第2个研究目的和创新之处。
收缩估计的基本思想是利用已知估计值作为起点,根据目标函数优化得到最优收缩强度,对当前估计值进行改进。已有研究结果表明,直接对组合权重进行收缩估计能够改善组合的样本外绩效。TU et al.[33]以等权重组合作为收缩估计起点,以基于样本矩的均值-方差组合作为优化目标;DEMIGUEL et al.[26]以最小方差组合作为收缩估计起点,以基于样本矩的均值-方差组合作为优化目标。这两种收缩估计做法均能改善均值-方差组合的样本外绩效,因此本研究采用收缩估计方法构建投资组合,并给出最优收缩强度的估计值。
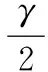
L(w*,wS)=U(w*)-E[U(wS)]

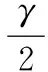
(2)
以最小化损失函数L(w*,wS)为目标,优化得到收缩密度δ。在损失函数左右两边同时对δ求导,根据一阶条件,得到最优收缩密度δ*为
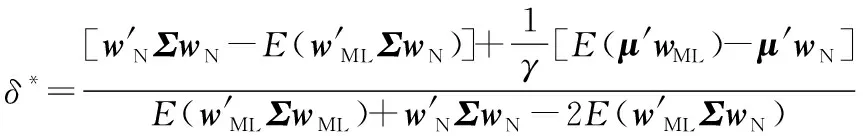
(3)

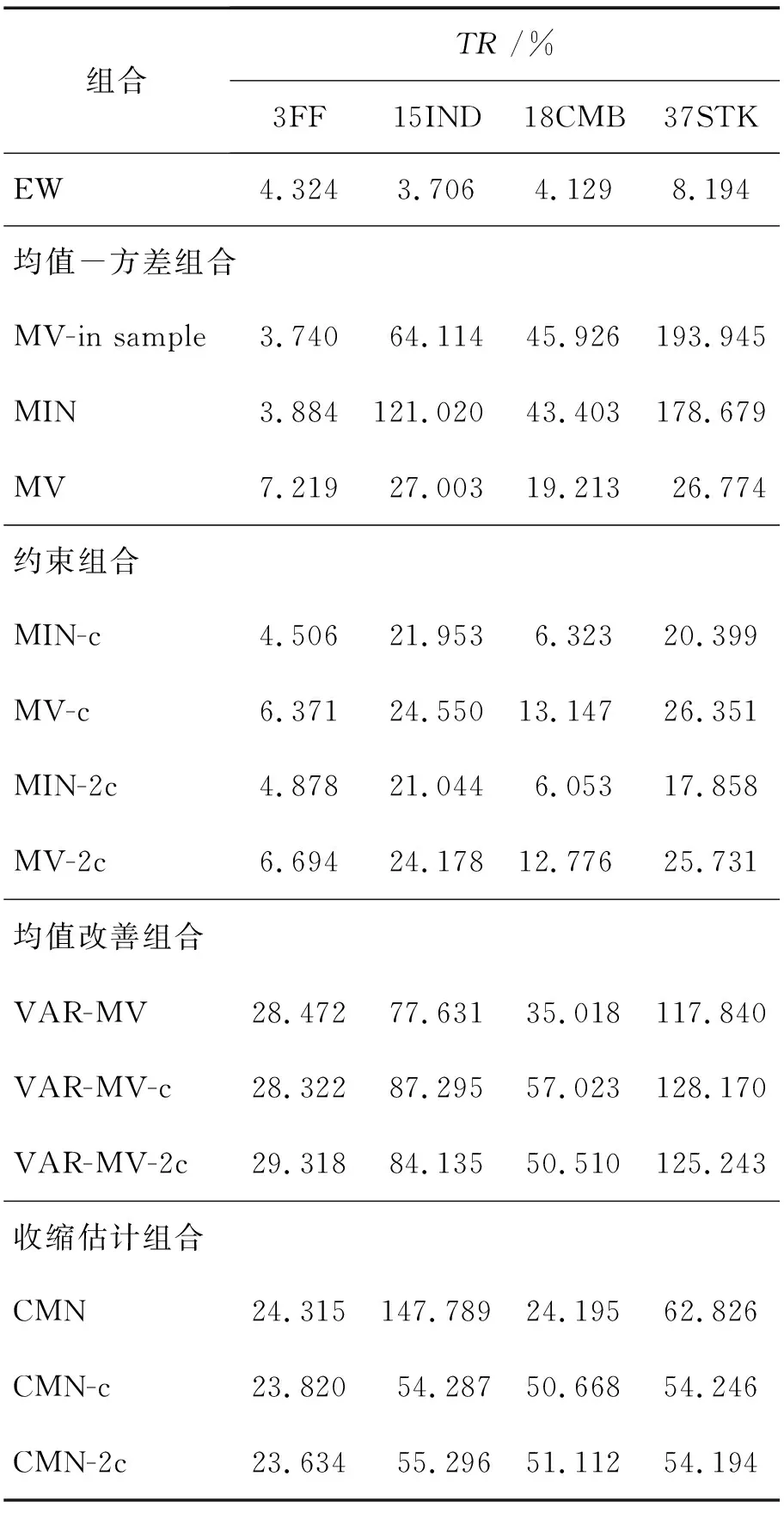
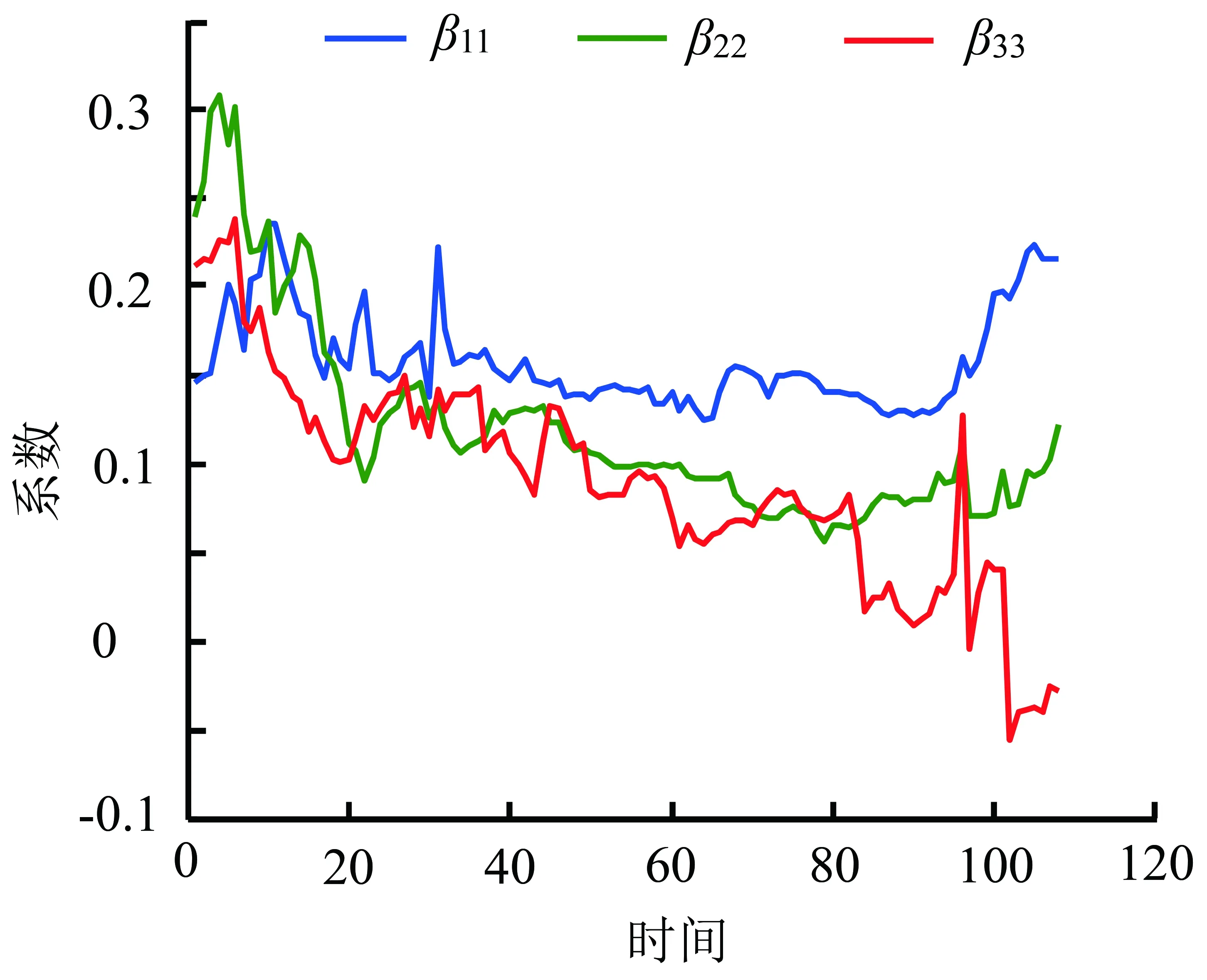
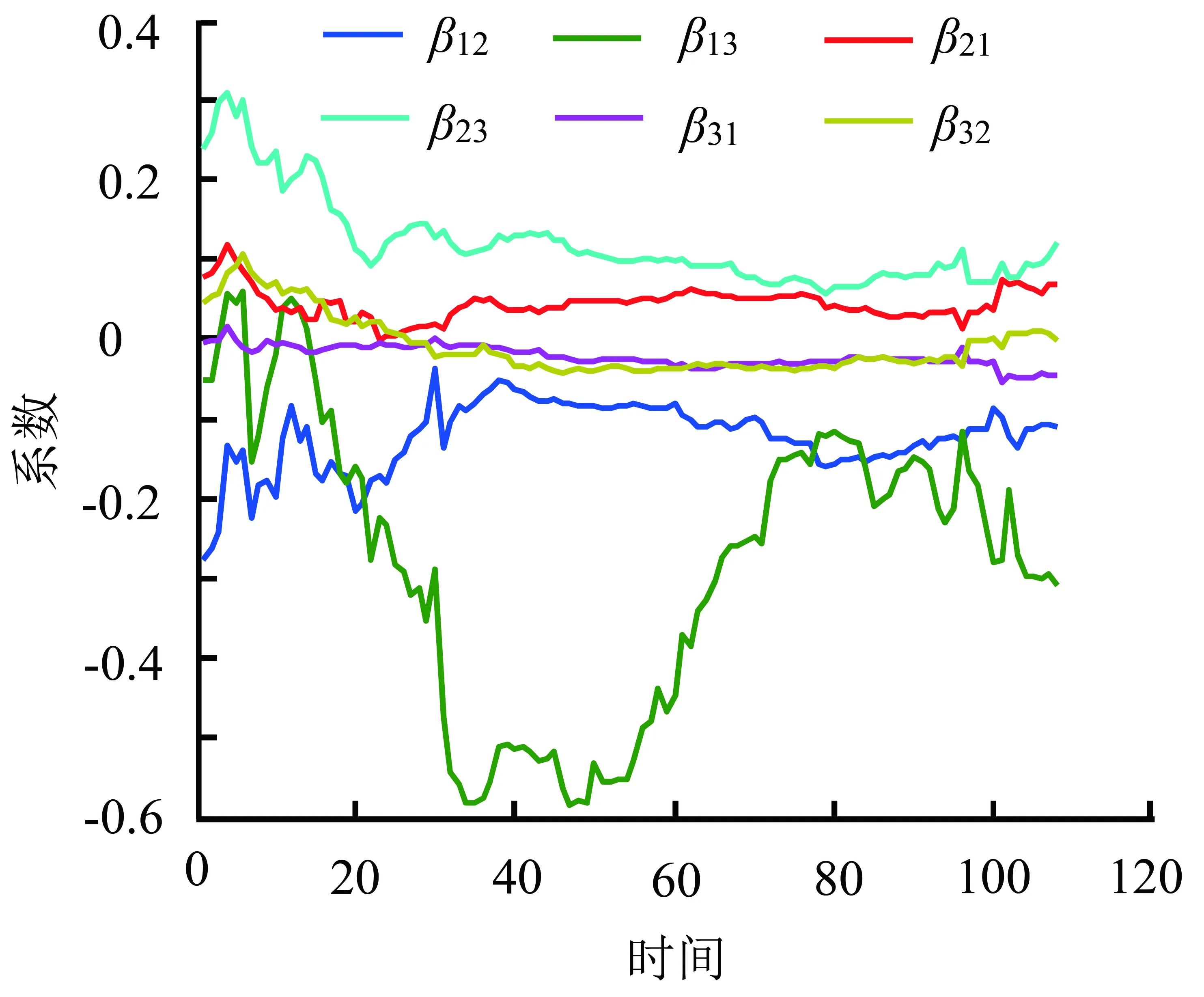
引理1函数f(x)在区间[a,b]上有定义,f(x)′和f(x)″存在,那么对于任意x1∈(a,b),如果f(x1)′=0,f(x)″>0,则有f(x1) 证明:先证明δ*∈(0,1)。 (4) 因此,δ*<1。 (5) 根据引理1,得证。 定理1表明wML和wN在满足特定的条件时,基于两者的收缩估计组合wS损失函数值最小,即理论上wS能够取得好于wML和wN的绩效。由于wN权重稳定,换手率较小,因此以该组合为收缩起点,能够有效降低组合的换手率,从而降低交易成本。进一步地,为了减少估计误差,得到绩效更加稳健的组合,考虑wML为VAR模型改善组合wV的情形,wV可分别代表VAR-MV组合、VAR-MV-c组合和VAR-MV-2c组合。根据定理1,可以得到当最优收缩强度δ*∈(0,1)时,收缩组合的期望损失更优。将wML=wV代入(3)式,得到最优收缩估计强度为 (6) (7) (8) 由于wV不存在解析解,δ*∈(0,1)需要满足的条件很难给出简洁形式,本研究只给出一种δ*不存在的特例。 证明:根据(6)式,当wN=w*时,(wN-w*)′Σ(wN-w*)-(wN-w*)′ΣE(wV-w*)=0,因此,δ*=0成立。得证。 定理2表明,如果等权重组合不等于真实最优组合,收缩组合能够降低组合后悔度,提高收缩组合的绩效。现实中定理2的条件很容易满足,因为等权重组合等于最优组合的概率并不是1。很多时候,样本内的均值-方差组合可以取得高于等权重组合的绩效[6]。 本研究从理论上说明收缩估计方法能够改进资产组合构建过程中的估计误差,从而提高对应组合的样本外绩效。实证上,本研究将通过对比投资组合的样本外绩效,检验VAR模型预测值是否是一个更好的期望收益估计值,以说明序列相关性对资产组合样本外绩效的改善。据此,本研究给出3个实证中的预期结果:①由于估计误差的存在,均值-方差模型在样本外绩效较差;②由于VAR模型预测值利用了序列相关性,是一个更好的期望收益估计值,因此期望收益估计改进模型的样本外绩效显著好于相同约束下基于历史均值的资产组合;③收缩估计改进的模型以等权重组合为收缩估计起点,因此收缩估计改进的模型能够大幅度降低期望收益估计改进模型的换手率,并且最优收缩估计值总处于[0,1]区间内,这是2.3部分证明的结果。 为了与已有研究的实证结果对比,本研究选择表1中的14种投资组合进行实证分析。由于1996年以前中国的上市股票数目较少,市场机制不完全,因此选取数据区间为1997年1月至2015年12月,共计228个月,这是目前相关研究中选用时间跨度最长的数据集。本研究选用月度超额收益进行投资组合绩效评估,数据来源于国泰安数据库。本研究选取4组中国A股市场数据集,第1个数据集是中国三因子数据,依据上市公司流通市值编制;第2个数据集是中国15个行业月度收益数据,依据中国证监会2012年行业分类标准进行行业分类,按照上市公司流通市值加权,月度数据缺失的公司在计算当月行业收益时予以剔除;第3个数据集是前两个数据集的组合;第4个数据集是中国A股市场37家上市公司月度收益数据,选取标准是2000年至2015年间月度数据没有缺失的37家非制造业上市企业,同期制造业上市公司数为51家,考虑到估计窗口为60个月,因此将制造业企业去掉,以减轻估计误差的影响。个股数据区间从2000年开始,这与黄琼等[8]在个股上的研究一致。以上4组数据集列示在表2中。 表1各种估计误差改进模型Table 1Various Estimation-error Improving Models 表2中国A股市场数据集Table 2Datasets on Chinese A Share Stocks CEQ定义为 (9) 其中,μk为k资产组合的超额收益均值,σk为k组合的标准差。wk的CEQ越高,其与U(w*)的差值就越小,则wk更优。本研究采用滚动窗口估计方法对选取的投资组合进行估计,滚动窗口长度分别选取60个月和120个月,范数约束的阈值为0.150,并取风险厌恶系数γ为2。 引入收缩估计组合的另一个目的是降低收缩估计组合的换手率,换手率越低,资产受到交易成本的影响越小。因此,在具有相同CEQ表现下,换手率更低的资产组合更优。定义k资产组合的换手率为 (10) 对于动态投资的实证,影响绩效最关键的因素之一是交易成本,交易成本的测量方法主要有买卖报价和比例交易成本[34]。考虑到数据可得性,本研究采用比例交易成本的方法。考虑交易成本后的k资产组合收益为 (11) 其中,κ为比例交易成本。实证中设定κ为0.050%。此外,本研究将κ取值为0和0.100%的情形作为稳健性检验。 3.2.1投资组合的样本外绩效 表3给出窗口期为60个月的各投资组合的样本外绩效。除样本内均值-方差组合外,CEQ最高的前两个组合用黑色字体标出。 首先,相对于均值-方差组合,EW组合在所有数据集上都有较好的样本外绩效。①对比EW组合与MV-in sample组合,在没有估计误差的情况下,样本内均值-方差组合绩效基本好于EW组合。②EW组合CEQ高于MIN组合和MV组合,说明估计误差严重影响了均值-方差理论在资产配置中的效果。综合上述两条发现,肯定了2.3部分的第1条预期结果。③卖空约束能够改善最小方差组合的样本外绩效。 MIN-c组合和MIN-2c组合绩效在多数情况下略好于MIN组合。这些结论与先前研究[6,8]的结论一致。 表3各组合样本外CEQ(Ⅰ)Table 3Out-of-sample CEQ of Various Portfolios(Ⅰ) 注:交易成本为0.050%,范数约束阈值为0.150,窗口期为60。 其次,施加范数约束和LW方差估计在A股市场作用比较有限。对比MIN-c组合与MV-c组合,除了37STK数据集,MV-c组合CEQ都高于MIN-c组合。MIN-2c组合与MV-2c组合也呈现出类似的现象,说明在范数约束下,将均值纳入目标函数有助于提高投资组合绩效。个股估计误差大于组合估计误差,这一点可能有助于解释37STK上较低的CEQ值。对比MIN-c组合与MIN-2c组合,发现样本方差与LW方差的绩效相当,说明LW方差的作用相对有限。这两点进一步肯定了EW组合是资本市场中一个良好的投资组合。 再次,相对于样本均值,VAR模型的预测值是期望收益更好的估计值。对比MV-c组合与VAR-MV-c组合,VAR-MV-c组合在所有数据集上都取得了高于MV-c组合的CEQ值。对比MV-2c组合与VAR-MV-2c组合,VAR-MV-2c组合的CEQ值均高于MV-2c组合。说明序列相关性有助于改善投资组合的样本外绩效,肯定了2.3部分的第2条预期结果。 最后,收缩估计组合比均值改善组合更加稳健。①没有施加约束的CMN组合的CEQ值最低,施加空头约束后,组合绩效得到了提高。②对比收缩估计组合与EW组合,CMN-c组合和CMN-2c组合均取得了高于EW组合的样本外绩效,CMN组合也取得了与EW组合接近的CEQ值。③分别对比均值改善组合与收缩估计组合,在3FF和15IND数据集,除CMN组合外,收缩估计组合的CEQ低于均值改善组合,但在18CMB和37STK数据集上,收缩估计组合的CEQ高于均值改善组合。特别地,CMN-c组合和CMN-2c组合在18CMB和37STK数据集上取得了高于EW组合和对应均值改善组合的CEQ值,这肯定了收缩估计方法在提高资产组合绩效方面的有效性。TU et al.[33]认为,如果δ有显式解,收缩估计方法对资产组合绩效的改善效果会更好。显式解的缺失可能是收缩估计组合在3FF和15IND数据集上表现较弱的原因之一。 3.2.2稳健性检验 表4给出窗口期为120个月的各组合的样本外绩效表现。表4的结果表明,估计窗口长度的增加有助于降低估计误差。①在3FF、15IND和18CMB数据集上,各投资组合的CEQ值均有增加,这与已有研究一致。②在37STK数据集上,各投资组合的CEQ有升有降,这可能与样本区间股票表现有关。因为窗口期为60时,样本外区间为2002年至2015年间的168个月,窗口期为120时,样本外区间为2007年至2015年间的108个月。两个区间内个股走势可能会有很大不同。③在多数数据集上,EW组合的CEQ值依然比均值-方差组合和约束组合更好。④关于均值改善组合和收缩估计组合的结论在窗口期为120个月的条件下仍然成立。在所有数据集上,VAR-MV-c组合的CEQ值大于MV-c组合,VAR-MV-2c组合的CEQ值大于MV-2c组合,说明引入VAR模型有助于降低来自均值的估计误差。特别是在3FF、15IND和18CMB数据集上,VAR-MV-c组合和VAR-MV-2c组合CEQ值好于EW组合。 另外,收缩估计组合表现十分稳健。不管在窗口期为60还是在120的情形中,收缩估计组合总是可以取得不弱于EW组合的CEQ值,特别是CMN-c和CMN-2c组合几乎在所有数据集上都取得了高于EW组合的CEQ值。 表5给出窗口期为60的情形下各组合的换手率。 ①对比同一组合在不同数据集上的换手率,同一组合在37STK数据集上的换手率比其他数据集上的更高。以EW组合为例,3FF数据集上的换手率为4.324%,而37STK数据集上换手率为8.194%,说明个股数据集上组合权重的波动性更大。而MV组合和均值改善组合在37STK数据集上的绩效都不理想,即不论是样本均值,还是VAR模型预测值,当波动性很大时,来自期望收益的估计误差都很大。对于VAR模型而言,可能的原因是波动性降低了期望收益估计的准确度。 表4各组合样本外CEQ(Ⅱ)Table 4Out-of-sample CEQ of Various Portfolios(Ⅱ) 注:交易成本为0.050%,范数约束阈值为0.150,窗口期为120。 ②约束组合的换手率相对较低。对比MIN组合和MV组合与约束组合,发现施加约束后,投资组合的换手率倾向于降低。 ③均值改善组合对期望收益估计误差的改善带来了换手率的大幅提高。对比约束组合与均值改善组合,均值改善组合的换手率最少提高了15.805%。 表5各组合的换手率Table 5Turnover for Various Portfolios 注:窗口期为60。 ④收缩估计组合能够降低均值改善组合的换手率。与均值改善组合相比,收缩估计组合几乎都低于均值改善组合。而表3和表4表明,相对于EW组合,受约束的收缩估计组合能够取得更高的CEQ值。 此外,本研究还进行了稳健性检验。①将风险厌恶系数γ分别调整为1、3、4和5,也可以得到类似的结论。②将范数约束的阈值调整为10%,对于结果的影响并不大。③在比例交易成本下,10基点以下的交易成本对于收缩估计组合CEQ值的影响并不大。这是因为本研究再平衡周期为1个月,而DEMIGUEL et al.[34]的研究中再平衡周期为交易日,从而本研究受交易成本影响更小。限于篇幅,不再报告这些结果,有兴趣的读者可以向作者索取。 为了进一步说明VAR模型对序列相关性的刻画,以3FF数据集为例,说明VAR模型的估计结果及其显著性。3FF数据集中包括MKT因子、SMB因子和HML因子。图1和图2给出VAR模型((1)式)估计系数中刻画自相关关系和横截面相关关系的估计结果,窗口期为120。 图2VAR模型中横截面相关回归系数Figure 2Regression Cross-sectional Correlation Coefficients of VAR Model 从自相关关系看,系数β11和β22均为正值,说明MKT因子和SMB因子均表现出正的自相关关系,而HML因子则表现出负的自相关关系。系数β33小于β11和β22,说明HML因子的自相关关系弱于MKT因子和SMB因子。从横截面相关关系看,表征横截面相关关系的回归系数波动性比表征自相关关系的回归系数波动性更大。系数β12和β13基本为负值,说明SMB因子和HML因子对未来1期MKT因子具有反向的相关关系;系数β21和β23均为正值,说明MKT因子和HML因子对未来1期SMB因子具有正向的相关关系;系数β31和β32绝对值较小,在0值左右,说明MKT因子和SMB因子对未来1期HML因子的预测能力不强。因此,同时考虑自相关关系和横截面相关关系的VAR模型更适合刻画收益率的序列相关性。 为了判断VAR模型是否能够有效刻画收益率的相关性,除了考虑回归系数的大小和变化情况以外,还需要考虑回归系数的显著性。系数显著性检验结果表明,VAR模型在大多数情况下也是显著的。在15IND、18CMB和37STK数据集上,所有的情形中VAR模型非截距项回归系数均至少有一个系数显著,逐一回归的F值至少有一个显著。结合VAR模型的回归系数和显著性,本研究认为VAR模型能够较好地刻画股票收益的序列相关性。而3FF数据集上VAR模型的显著性水平较差,可能的原因是数据集和估计区间长度不同。首先,本研究选用Fama-French三因素作为输入变量,而DEMIGUEL et al.[34]采用Fama-French 2×3分组资产组合数据集,三因素之间的相关性较分组资产组合更低,输入变量更少;其次,本研究采用月度收益,估计区间长度为120个月,而DEMIGUEL et al.[34]采用2 000个交易日作为估计区间,更长的估计区间长度可以得到更加稳定的估计系数。 在3.2部分的实证结果中,均值改善组合在个股组合上的改善效果并不理想,可能的原因是期望收益的估计误差在个股数据集上更大。本节通过预测误差讨论估计区间长度对均值预测的影响效果,需要强调的是,预测误差并不等同于期望收益的估计误差,因为在非仿真条件下,确定真实期望收益是困难的,预测误差在一定程度上可以反映来自期望收益的估计误差情况。表6给出不同估计窗口下VAR模型的预测误差,结果表明,①在个股数据集上,随着估计窗口长度的增加,VAR模型的预测误差呈现下降趋势,说明估计窗口的增加有助于改善均值的估计误差;②个股数据集上的预测误差均大于组合数据集上的预测误差,这与3.2部分均值改善模型在个股数据集上表现不好的现象一致。 可能的原因有两个,①个股收益的序列相关性较弱,使VAR模型的预测并不准确;②个股波动性更大,增加了期望收益估计的难度。这是因为VAR模型利用收益序列的相关性改善期望收益的估计,特别是收益序列的一阶自相关关系。相关性越强,对均值估计改善的效果就越好。首先,3.2节换手率分析的结果表明,37STK数据集上的换手率高于其他数据集上的换手率。而37STK数据集上平均年化波动率约为47.740%,其他数据集上平均年化波动率为31.741%,这肯定了37STK数据集上波动性更高。其次,根据ACF检验的结果,18CMB数据集包含的3因子和证监会15个行业收益序列均存在10%水平上显著的一阶自相关关系,而37STK数据集包含的37只个股只有2只存在10%水平上显著的一阶自相关关系,7只存在15%水平上显著的一阶自相关关系。因此,高波动性和弱相关关系可能都减弱了VAR模型对于期望收益估计误差的改善效果。 表6VAR模型预测误差与估计窗口长度Table 6Prediction Error in VAR Model and Length of Estimation Window 表7最优收缩强度分布统计Table 7Distribution Statistics of Optimal Shrinkage Tension 注:窗口期为60。 本研究从资产收益序列的相关性出发,将VAR模型应用到均值-方差模型的期望收益估计中,利用收缩组合方法克服均值改善组合绩效不稳定和较高换手率的缺点,给出最优收缩强度的估计值,从理论和实证两个方面分析收缩估计组合在提高投资组合绩效方面的作用,得到如下研究结论。 (1)序列相关性有助于提高证券投资组合的样本外绩效。与样本均值相比,考虑收益序列相关性的VAR模型预测值可以减少期望收益的估计误差,均值改善组合可以取得高于相应条件下的均值-方差组合。在一些数据集上,均值改善组合还能够获得优于等权重组合的绩效。 (2)收缩估计方法能够减弱均值估计改善带来的更高换手率和不稳定的绩效表现。收缩估计方法能够降低均值改善组合的换手率,在样本外绩效和换手率之间取得较好的平衡。对最优收缩强度的分析结果表明,在81.250%以上的情形下,VaR-MV-2c组合的最优收缩强度的估计值处于(0,1)内,说明收缩估计方法在大部分情形中可以改进组合的估计误差。 综上,本研究结果对缓解参数不确定性的影响、减少资产组合构建过程中估计误差、提高投资者的效用具有一定的参考意义。本研究没有对序列相关性的形式进行假定,优化问题的复杂性使均值改善模型缺乏显式解,因此最优收缩强度没有给出显式解,是本研究的一个不足。除了一阶矩以外,考虑高阶矩[43],对序列相关性进行更精细的模型假定,得到均值改善模型的显式解,将更多误差减少方法和其他市场异象引入均值-方差理论的参数估计改善中,是未来可能的研究方向,如证券订单簿信息[44]和投资者情绪指数情况[45]等量化指标。
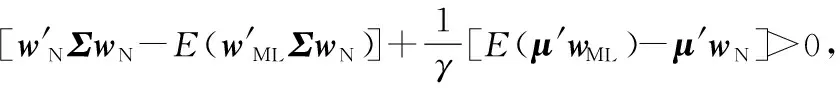
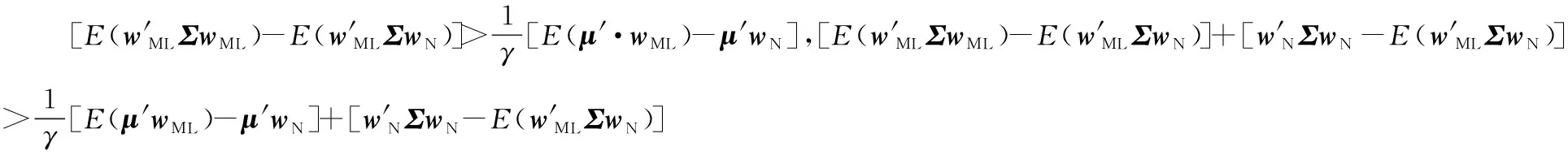


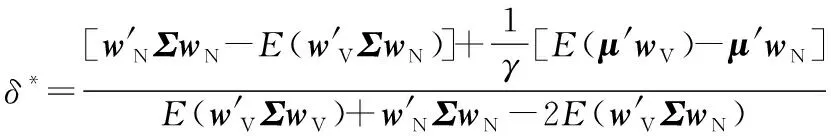


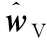


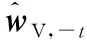

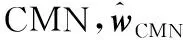


3中国资本市场实证结果
3.1实证数据和方法

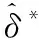

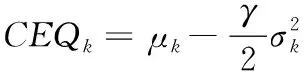
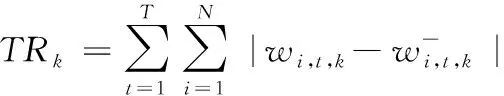
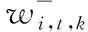

3.2实证结果分析


4进一步分析
4.1VAR模型回归结果
4.2均值改善组合绩效的影响因素分析

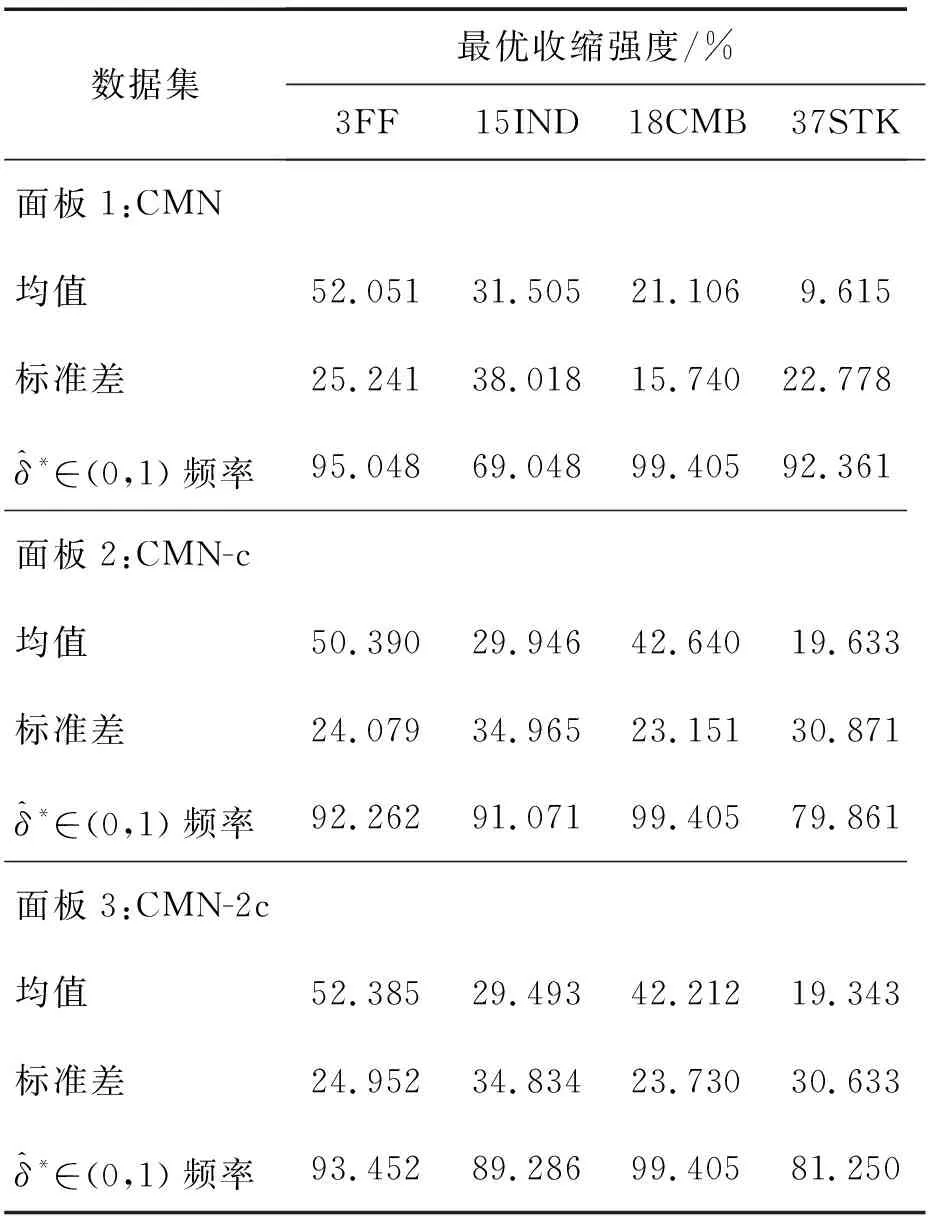
4.3收缩估计组合的最优收缩强度分析

5结论

