斜拉桥力学综合测试实验开发与实践

王斐斐, 周 博, 薛世峰

(中国石油大学(华东) 储运与建筑工程学院, 山东 青岛 266580)

新工科的建设的关键任务之一就是强化实践能力和创新创业能力的培养,要求延展实践育人平台,强化教学实验、科学实践、实习实训[1]。为适应“新工科”建设要求,有必要对现有传统实验教学体系和方法进行改革。

打破传统的教师按照固定的模式向学生传授实验知识和方法的力学实验教学方式[2-5],基于不同学科工程背景,结合材料力学理论知识和现有力学实验测试技术,开发学科交叉、创新型、综合型力学教学实验项目,在强化学生工程意识、培养学生工程创新能力方面有很好的促进作用,非常适合“新工科”理念下创新能力和跨界整合能力人才的培养。

斜拉桥的力学分析属于典型工程实际问题[6-9],因此该实验依据相似原理和量纲分析法获得模型与原型相似常数,经选材、加工建成斜拉桥模型,开发了斜拉桥力学综合测试实验。该实验涵盖了工程中力学问题分析的重要环节:工程问题-力学建模-理论计算-力学测试-结构优化,是力学理论知识与工程问题的有效结合,适应了“新工科”创新型卓越工程人才培养的需求,获得了良好的教学实践效果。

1 斜拉桥的力学建模及加工

选取河南省王楼(省界)至兰考高速公路第二合同段的斜拉桥为斜拉桥原型,桥净宽7 m,桥梁全长110 m,上部结构采用20 m+32 m+32 m+20 m预应力钢筋混凝土斜拉桥-连续梁组合体系,塔墩梁固结。主梁采用单箱双室截面,梁高1.0 m,边腹板厚80 cm,翼缘板悬臂长为35 cm,顶板厚20 cm,底板厚20 cm。端横梁宽1.0 m,墩顶中横梁宽1.2 m,塔墩中横梁宽2.0 m。桥塔采用H型塔,矩形实心截面,上部宽1.3 m,根部宽1.7 m。桥面以上上塔柱高18 m,下塔柱高8.5 m,全高26.5 m,并设置上、下横梁各一道,上横梁高1.2 m，下横梁高1.5 m,与主梁一同浇筑。斜拉索采用OVM200级钢绞线拉索,钢绞线标准强度为1 860 MPa。梁上标准索距4 m,塔上标准索距1.6 m,单塔双索面扇形布置,全桥共计24根OVM15-7规格的拉索。

1.1 基于相似理论的斜拉桥力学建模

相似理论的主要内容是确定结构模型的相似条件和相似结构。依据力学理论,引起原型或模型力学行为的物理力学因素之间存在着内在的联系,即各物理量因素要受力学基本方程的约束。在模型设计和加工过程中,需要简化或者忽略部分次要参数,且模型实验有多种分类,该实验主要考虑动、静荷载下的模型实验,相似关系应满足静力相似和动力相似关系,主要涉及尺寸相似、刚度相似、容重相似,同时还需满足弹性模量、位移、力、应力截面及截面惯性矩等的相似。

1.1.1 静力相似关系

斜拉桥是超静定无限自由度的复杂结构,其确切的理论分析非常复杂,实际工程中对其做简化,其整体分析一般采用平面杆系有限元法。对单元刚度矩阵方程做量纲分析,结合材料力学的本构方程,能得出模型所需的静力相似关系[9]。选取缩尺比S和弹性模量相似比SE作为基本量,其他物理量的相似关系用这2个比值来表示。根据杆系有限单元法,由梁杆的单元刚度方程可得式(1),由材料力学公式(2)、(3)和式(4)可得式(5)—式(6):

(1)

(2)

σ=Eε

(3)

γAL=P

(4)

(5)

(6)

式中：P、M分别为集中力和弯矩；γ、E分别为材料容重与弹性模量；σ、ε、δ、ψ分别为应力、应变、线应变和角位移；L、A、W、I分别为单元几何尺寸、截面积、抗扭截面系数、截面极惯性矩。

通过梁杆的单元刚度方程以及材料力学公式得到的相似准数,可推导出静力模型相似关系如下:

SEA=SES2,SEI=SES4,SM=SEW=SES3

(7)

(8)

1.1.2 动力相似关系

除应满足静力相似的条件外,还需满足与动力问题相关的物理参量的相似条件[10]。斜拉桥属于多次超静定复杂结构,难以明确给出其运动方程,考虑影响其结构动力响应的物理量,故采用π定理分析动力相关系。采用量纲分析的方法,建立各物理量的关系(见式(9)),而后通过量纲矩阵和π矩阵得到7个相似判据(式(见10)—(11)):

f(H,δ,ρ,ω,μ,a,l,F,υ,E)=0

(9)

(10)

(11)

式中：H为位移传递系数；δ为位移；ω为圆频率；ρ为质量密度；υ为泊松比；a为加速度；l为线性尺寸；F为外力；v为速度；E为弹性模量。

(12)

Sσ=SE,Sε=Sa=Sμ=1

(13)

(14)

综合考虑材料、实验室空间以及测试设备等因素,确定几何缩尺比采用1∶50进行设计加工。模型材料的确定应尽量接近或同实际斜拉桥有一定程度的相似,性能稳定,强度高而弹性模量低,且易于加工。鉴于此,该桥的桥梁和桥塔选用的是铝合金,铝合金和混凝土的弹性模量之比为2∶1。继而得到几何相似常数Sa=1/50,SE=2。主要物理量相似常数见表1。

表1 斜拉桥模型主要参数的相似比

1.2 斜拉桥模型设计与加工

一种单塔双面斜拉桥试验模型,主要包括主塔、主梁、斜拉索、桥墩、桥面、斜拉索锚固螺帽、索力调整装置(见图1),其中索力调整装置还包括螺母、套筒及锚固等细部构件。主梁采用4根截面为10 mm×10 mm×1 028 mm的实心铝方柱。为增强桥梁的整体性,防止主梁在加载过程中失稳,桥梁之间用8根截面为10 mm×10 mm的实心铝方柱拼装而成。主塔及桥墩采用25 mm×25 mm实心铝方柱,主塔的结构形式为由两根塔柱组成的门式框架。塔墩、塔梁固结,成为具有多弹性支撑的四跨连续梁。

图1 斜拉桥模型的立体结构CAD图

索力调整装置见图2,在两边螺杆正中心位置钻2 mm孔,穿过钢丝并锚固,套筒中部位置可以通过贴应变片应用电测法间接测得索力。斜拉索采用直径为1.2 mm高强钢丝绳,为方便配重及模型美观,桥面采用4 mm厚有机玻璃。为保证桥面水平,桥墩及桥塔底部承接在一块长2 m的实木板上。为使模型实际制作方便,将原型的箱型主梁简化为2个等截面的小箱型梁,并通过横隔梁连接,横隔梁的截面形式与尺寸同主梁,主塔与梁等所采用的材料均是市场上现有规格的方柱铝材。模型材料及加工工艺见表2。建成的斜拉桥模型见图3。

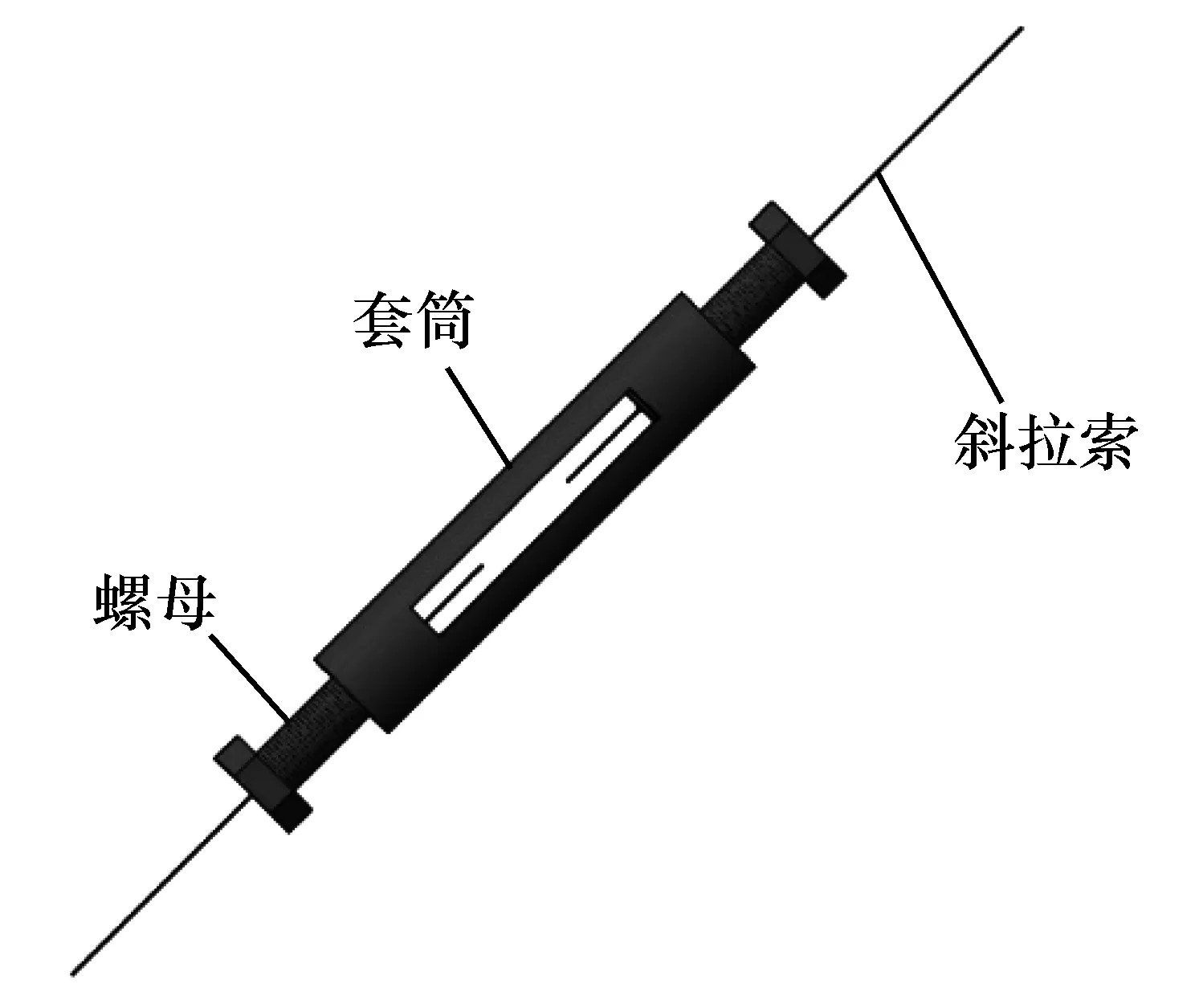
图2 斜拉桥模型的索力调整装置

表2 模型材料及加工工艺

图3 加工建成的斜拉桥模型

2 斜拉桥模型用于实验教学的可行性测试

2.1 用于静力测试的模型配重设计

原型与模型的容重相似比为λγ,通常λγ为一个较大的常数,在实际中很难找到容重如此大的材料,因此,就需要通过配重的方式来增大模型结构的换算容重,使其满足容重相似比的要求。根据相似原理,模型每延米需要配重W′。

W′=(λγλp-λm)Am

(15)

式中，λp为原结构构件的换算容重,λm、Am分别为模型相应构件的容重和截面积。

图4是在配重基础上进行某工况实验的现场图片。配重共5个定位点,沿桥身均匀布置,1、2、4、5号点各配重5 kg砝码,考虑主塔影响以及砝码数量限制,3号位置即主梁与主塔连接部位,两侧对称布置2×2.86 kg的岩心。其他工况均在配重基础上分级加载,卸载时不卸载配重。

2.2 斜拉桥模型静力电测实验

图4 斜拉桥模型配重与测试现场图

运用电测实验方法,在桥身关键位置布置了19个观测点(见图5)。测点沿主梁、各横梁、主塔及桥墩布置,以观测在自重及局部荷载作用下的应力、应变分布规律,同时在主跨跨中设置千分表以观测挠度的变化。

图5 斜拉桥模型测点布置图

静载实验根据测点布置选取7个加载工况分级(见表3)加载。工况1:配重荷载均匀对称加载；工况2:边跨跨中集中力两边对称加载；工况3:边跨跨中集中力一边加载；工况4:主跨跨中集中力两边对称加载；工况5:主跨跨中集中力一边加载；工况6:边跨+主跨跨中集中力对称加载；工况7:边跨+主跨跨中集中力一边加载。

表3 不同工况与分级加载

实验测试最终得到了18个测点的有效数据。由于数据量大,本文取工况2和工况7的测试结果绘制了不同测点处应力的分布规律曲线,见图6和图7。“工况2-1”代表工况2情况下施加第一级荷载,“工况2-2”代表工况2在第一级载荷作用下继续施加第二级荷载,“工况2-3”代表工况2在第一、二级载荷作用下继续施加第三级荷载。

图6 工况2分级加载下的应变分布规律

由图6可见,工况2在边跨跨中集中荷载对称布置情况下,桥梁跨中位置均出现峰值,且峰值接近,沿主梁方向应变响应基本呈现对称分布的规律。

由图7可见,工况7为边跨+主跨跨中集中力一边加载,结构在加载位置应变最大,在远端最小,且在主跨跨中从左向右出现2个递减的峰值,符合结构力学原理。工况7-3,在主跨跨度远大于边跨跨度的情况下,相同荷载下边跨跨中的应变大于主跨跨中的应变,说明斜拉索参与受力,且随着荷载的增大斜拉索的作用越来越明显,改善了结构受力。同样,在连接主梁的横梁跨中也很好地表现出同样的规律。

图7 工况7分级加载下的应变分布规律

通过对模型的静力加载测试,进行了单塔双面斜拉桥在自重及不利荷载作用下结构力学反应的模拟。结果显示,在外力增大的情况下,斜拉索参与受力的程度越来越高,起到了优化结构受力的作用,与真实斜拉桥结构的受力状况规律基本相符。

3 斜拉桥力学综合测试实验的教学应用

斜拉桥力学综合测试实验提供了一种将具体的工程实际问题转化为相应力学问题进行分析的思路和方法,并且该模型实验能够帮助学生综合运用材料力学的重要理论及实验测试方法。根据实验教学要求和学时的不同,我们将该实验部分或整体引入到现有实验教学中(图8为学生采用静态电阻应变仪进行线路连接与测点布置的现场),在中国石油大学(华东)力学实验教学中取得了良好的效果。

图8 学生采用电测法进行斜拉桥测试实验

可进行的具体实验如下：

(1) 斜拉桥模型设计与制备的实验。在其CAD图纸以及相关数据基础上,依据相似原理进行模型相似和动力相似的推导获得模型参数相似比,绘制模型CAD图,而后选择合适的材料进行设计加工,建立可以进行不同力学工况下物理实验与测试的斜拉桥模型,是一个相对完整的力学建模过程。该实验有助于学生更加深入理解典型工程问题与材料力学理论知识的有效密切结合,亦能掌握力学问题分析的方法和步骤。该实验项目需8～10学时。

(2) 运用理论计算方法与电测法进行斜拉桥力学测试实验。学生可以在已有模型的基础上,进行加载工况设计,计算和测试不同工况下的应力和变形情况。通过这一实验,有助于学生熟悉课堂理论知识在具体力学问题中的应用,也有助于学生更加熟练使用电测法进行力学测试。该实验项目需3～4学时。

(3) 斜拉桥模型的强度与结构优化实验。斜拉桥是一种桥面体系以加劲梁受压弯为主,支撑体系以斜拉索受拉及桥塔受压为主的桥梁,是一种高次超静定结构,其自重引起的内力和变形可以通过调整斜拉索的张拉力而人为地进行调整。综合(1)与(2)两个实验项目,可以开展包括模型设计、加工、计算、测试于一体的综合性实验,有助于学生实践一个“工程问题—力学建模—理论计算—力学测试-结构优化”的完整过程,该实验项目需11～14学时。

4 结语

斜拉桥力学综合测试实验来源于典型的斜拉桥工程实际问题,其设计和分析过程包含了力学问题分析的重要环节“工程问题-力学建模-理论计算-力学测试-结构优化”,属于学科交叉、创新型、综合型教学实验。通过这一实验项目,学生综合运用了材料力学的超静定、组合变形、强度理论、应力状态等理论方法,熟练掌握了电测法测试技术,了解了复杂工程结构问题进行强度优化的基本方法。该实验锻炼了学生运用理论与实验方法结合实际问题的综合能力,实现了综合性、设计性、探索性相结合的实验教学要求,非常适合“新工科”以继承与创新、交叉与融合、创新型卓越工程人才培养的新要求。

该实验还可以跟数值模拟技术相结合,实现实验测试与数值模拟结果的相互验证与对照[11-12],可以面向已经学习过ANSYS、ABAQUS等数值模拟软件的高年级本科生开设这一实验项目,或者面向研究生开设该实验项目。

该斜拉桥力学综合测试实验还有进一步的发展空间。斜拉桥原型到模型的转换过程做了一些简化,如果对桥梁特定细节进行分析时,需根据不同需求进行细节的处理。模型的力学测试部分,只进行了特定载荷下的静力测试实验,该部分展示了一种测试思路和方法,如有动力测试或者其他测试需求,或者有其他测试技术手段,均可以在此方法上进行拓展。