带矩约束的二阶段分布式鲁棒优化
张 轩,韩有攀
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
近来,分布式鲁棒优化成为解决不确定问题的一个研究热点.该优化问题为:在不能准确得到随机变量概率分布的情况下,将概率分布限定在由分布的一些特征所构造的不确定集合(一阶矩、二阶矩信息、边际分布或者支撑集合的信息等)中,从而在该不确定集合下求最优.其关键是不确定集的构造,其构造遵循(1)包含真实数据,具有高置信度的分布.(2)应该在排除病态分布的情况下集合足够小.(3)易于参数化数据.理想情况下,应该易于转化为一个可求解的数学模型,可以用现成的优化软件求解.
分布式鲁棒优化首次应用是在1958年,Scarf[1]用于研究单个项目报童的分布问题,其中模糊集合由具有相同均值和方差的概率分布族组成.随后,该模型被Breton[2]推广到动态极大极小随机规划问题中.在文献[3-4]中,不确定集包含某些给定约束条件的单峰分布,且在一定条件下最坏分布为均匀分布.文献[5]推广了以前无分布假设的报童问题,假设分布是关于均值和标准差的概率分布函数,给出了一个优化程序计算任意订货量下的最优订单.文献[6]提出优化问题中不确定集的分布形式可以由离散分布(高斯分布、指数分布等)和矩信息(均值和协方差)两种变量假设,并将该优化问题通过对偶原理等转化为可求解模型.文献[7-8]研究了带矩约束的二阶段分布式鲁棒优化模型,分别在有线性决策规则和无线性决策规则下,运用对偶原理将带矩约束的二阶段分布式鲁棒优化转化为可求解模型.Gao等[9]在前人研究的基础上引入高阶矩约束,用半无限规划方法求解带高阶矩约束的二阶段分布式鲁棒优化问题.
本文研究二阶段分布式鲁棒优化问题,在不确定集合由二阶矩构成且随机变量的样本空间由线性不等式构成情况下的可求解模型.分别对决策变量在线性决策规则和无线性决策规则两种不同情形下,通过对偶理论,给出相应的可求解等价模型.
1 二阶段分布式鲁棒优化
考虑模型
(1)
其中:式(1)中′为转置,第一阶段初始决策x=(x1,x2,…,xn),X={x:Bx=b,x≥0}⊆Rn,B∈Rq×n,b=(b1,b2,…,bq)∈Rq,Γ为不确定集.
第二阶段优化问题为
Q(x,z)= mind′y
s.t.A(z)x+D(z)y=b(z)
y≥0
(2)
其中:d=(d1,d2,…,dk)∈Rk,D(z)∈Rl×k为补偿矩阵,A(z)为技术矩阵,b(z)为右端项.
其不确定集由一阶矩和二阶矩约束确定
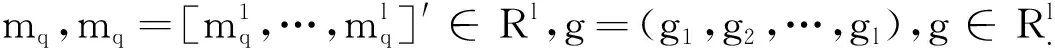
2 线性决策下的等价模型
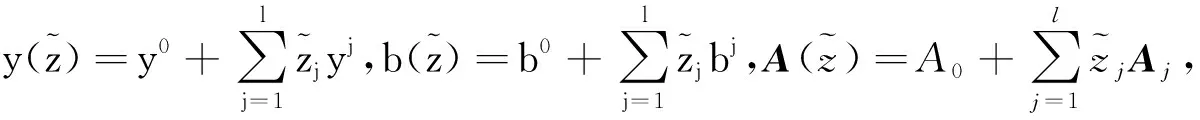
在上述条件假设下,考虑其中Q(x,z)为式(3)优化问题的最优值,即
Q(x,z)= mind′y
s.t.A(z)x+Dy=b(z)
y≥0
(3)
D∈Rl×k为固定的补偿矩阵.利用凸性、对偶理论、极大极小原理将优化问题式(1),(3)等价转化为可求解模型,其结果如下:
定理1 在线性决策下二阶段分布式鲁棒优化问题式(1),(3)等价于
证明利用线性对偶
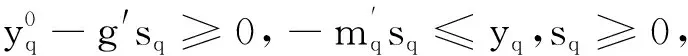
其中,s=(s1,s2,…,sk).则式(1),(3)变型为
将矩约束代入则为
根据文献[10]中无穷维线性规划对偶理论知,其对偶规划为
(4)
其中:v0∈R,v=(v1,v2,…,vl)∈Rl,V=(V1,V2,…,Vl)∈Rl,μ=(μ1,μ2,…,μl),η=(η1,η2,…,ηl).
由于Ω是一个凸的多面体集合,并且第二阶段优化问题是线性优化,其解集是凸集,参考文献[8],则式(4)中第一个约束条件∀z∈Ω.
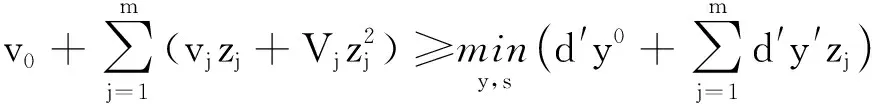
即
(5)
利用文献[11]中凸二次规划的Wolfe对偶性和变量的可分离性,式(5)等价于
整理为
(6)
其中,λj为新引入的对偶变量.
如果Vj>0,由2Vjzj+(vj-d′yj+Mjλj)=0得zj=-(vj-d′yj+Mjλj)/2Vj,
将其带入式(6)即
引入辅助变量rj,令rj=(vj-d′yj+Mjλj)2/4Vj,上式等价于
(7)
如果Vj=0,从式(6)直接推出式(7).
因此,式(1),(3)转化为
易得定理1.
定理1推广了带矩约束的二阶段分布式鲁棒优化,给出在更为复杂的情形下的可求解模型.不仅丰富了相应的理论成果,还为进一步解决复杂的实际问题提供了可行方法.
3 无线性决策下的等价模型
Q(x,z)考虑仅仅右端项随机的二阶段分布式鲁棒优化模型:
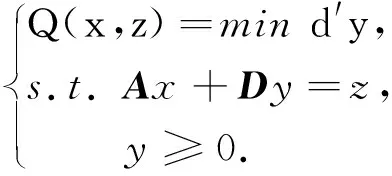
(8)
为了将优化问题式(1),(8)转化为易求解模型,需要假设以下3个条件:
条件2
条件3
条件1是对单纯形顶点的假设.条件2是极大极小值原理,若X是紧集时成立,详见文献[12].条件3是期望的最小值等于最小值的期望,若第二阶段函数有最优值且其解的集合为严格封闭的凸可测集时其成立,详见文献[13]的定理14.60.
引理1 在假设条件1-3成立情况下,下列等式成立
(9)
证明由条件2,3,优化问题式(1),(8)可进行变形:
结合条件1知上式等价于
(10)
由Γ表达形式可得
根据文献[10]中无穷维线性规划对偶理论,其对偶形式为
minv0,v,Vv0+μ′v+η′V,
s.t.v0+z′v+(z2)′V≥max1≤i≤m(z′ωi+b′ui),
v,V≥0,
z∈Ω.
(11)
其中,v0∈R,v=(v1,v2,…,vl)∈Rl,V=(V1,V2,…,Vl)∈Rl,μ=(μ1,μ2,…,μl),η=(η1,η2,…,ηl).
由于z是一个凸的多面体集合,并且其第二阶段优化问题的解集是凸集,式(11)等价于
min{v0+μ′v+η′V:v0+z′v+(z2)′V≥z′wi+b′ui,1≤i≤m,z∈Ω}.
证毕.
利用引理1将仅仅右端项随机的二阶段分布式鲁棒优化模型转化后,可以看出其类似于定理1中的式(5).通过凸二次规划的Wolfe对偶性和变量的可分离性,将其转化为可求解模型.
定理2 假设条件1~3成立,二阶段分布式鲁棒优化没有线性决策条件的优化式(1),(8)等价于一个二阶锥规划问题,即
证明由引理1知,式(11)约束条件为
v0+z′v+(z2)′V≥z′wi+b′ui,1≤i≤m,v≥0,V≥0,z∈Ω
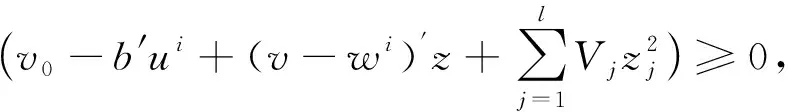
对于固定的i,由Ω={z∈Rl:Mz≤g}得
(12)
与定理1证明类似,上式等价于
即定理2得证.
4 结束语
在样本空间为多面体集合时,探讨决策变量服从线性决策规则和第二阶段问题中仅仅右端项为随机变量的情形,并给出了在这两种情形下二阶段分布式鲁棒优化问题等价于相应的二阶锥优化问题.为求解相应的带矩约束的二阶段分布式鲁棒优化问题提供了方法,而且为其应用到实际问题中奠定了基础.

