纯棉机织物透气性预测
孙浪涛
(泉州师范学院 纺织与服装学院,福建 泉州 362000)
0 引 言
织物透气性是指织物两侧存在压差时,空气从织物孔隙透过的能力,通常采用透气率来表示.透气率是在规定的试样面积、压降和时间条件下,气流垂直通过试样的速率[1].通过织物透气性预测,可以根据产品透气性需求设定织物规格,对纺织品的生产及使用具有指导意义.
织物透气性预测的方法主要有神经网络预测法[2-6]和公式计算法[7-9]两种.神经网络预测法是通过人工网络模型对所选取的影响因子进行拟合训练,采用神经网络算法可进行特定织物透气性预测.公式计算法是假定织物内纱线交织形成矩形孔隙,将织物这种多孔介质材料看成平行管束模型,采用流体力学理论中的Hagen-Poiseuille定律进行织物理论透气性计算,结合织物结构参数拟合得出预测公式,求得透气性预测值.两类方法在特定样本下得到的织物透气性预测值都能达到一定的预测精度,但公式计算法相较于神经网络预测法适用范围更广,且简单方便[9].根据流体力学理论中矩形风管当量直径换算办法,可以将矩形通道换算成等速当量直径和流量当量直径两种圆形通道,其中等速当量直径适用于层流及紊流过渡区,流量当量直径适用于紊流过渡区[10].文中采用公式计算法对纯棉机织物透气性能进行预测,对比分析两种织物孔径计算方法得到的透气率预测值与实测值之间的相关性,从而得到预测精度较高的一种织物透气率预测公式.
1 织物透气性分析与计算
空气透过织物的主要途径有织物内纱线间孔隙及纱线内纤维间孔隙两种,一般以前者为主[11-13].织物内纱线间的孔隙大多是相互贯通的,从织物一侧到另一侧,孔隙先减小后增大,呈现类似于方形截面但有瘦尖角,带螺旋的头对头的喇叭形状,使得气体流经织物常产生涡流,形成紊流运动[14].当气体透过织物时,其过程与流体流过多孔介质的过程类似,因此可以将其看成平行管束模型,采用流体力学理论中的Hagen-Poiseuille定律来进行织物透气性计算[15].假设织物内纱线交织产生的孔隙为矩形,且分布均匀、大小相同,根据流体力学理论,可以将纱线间的孔径转换为等速当量直径(dh)和流量当量直径(dl)两种,便于采用Hagen-Poiseuille定律计算.
1.1 等速当量直径
若a,b为矩形风管的边长,根据流体力学理论,等速当量直径[10]dh(mm)为

(1)
若Pj,Pw为织物经、纬密度(根/10 cm);dj,dw为织物经、纬纱线直径(mm).根据式(1)则有
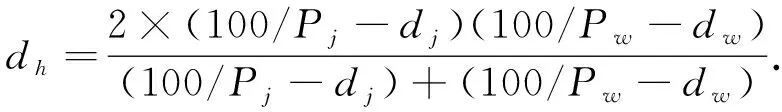
(2)
1.2 流量当量直径
根据流体力学理论,流量当量直径[10]dl(mm)为

(3)
根据式(3)则有
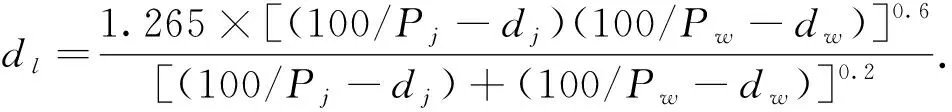
(4)
1.3 织物透气率计算
根据流体力学理论,空气流经单一圆管时,可采用Hagen-Poiseuille定律[7]来计算透气量

(5)
其中:q为透气量(m3·s-1);Δp为管两端的压差(Pa);l为圆管的长度(m);d为圆管的直径(m);μ为空气的动力黏度(Pa·s).
织物内单位面积的孔隙个数[7]为
n=(10Pj-1)(10Pw-1).
(6)
织物的透气率[7]为
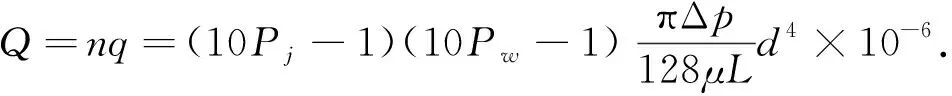
(7)
其中:n为孔隙个数(个·m-2);L为织物厚度(mm);Q为透气率(mm·s1).将等速当量直径dh及流量当量直径dl分别带入公式(7),便可得到织物的理论透气率Qh及理论透气率Ql.
2 实 验
2.1 材料与仪器
(1) 材料 平纹织物32种,测得织物参数见表1.

表 1 试样结构参数
(2) 仪器 YG461E型数字式织物透气量仪(泉州市美邦仪器有限公司),YG002型纤维细度综合分析仪(泉州市美邦仪器有限公司),YG141D型数字式织物厚度仪(泉州市美邦仪器有限公司),Y511B型织物密度镜.
2.2 测试方法
2.2.1 织物透气率 按照GB/T5453—1997《纺织品织物透气性的测试》,采用YG461E型数字式织物透气量仪测试织物透气率,试样面积为20 cm2,压降100 Pa,同一样品测试10次,取平均值,记为Qs.
2.2.2 织物厚度 按照GB/T3820—1997《纺织品和纺织制品厚度的测定》,采用YG141D型数字式织物厚度仪测量织物厚度,压脚面积2 000 mm2,压力100 cN,加压时间30 s,同一样品测试5次,取平均值.
2.2.3 纱线表观直径 采用YG002型纤维细度综合分析仪拍摄织物表面结构图片,测量织物中纱线的表观直径,同一样品测试20次,取平均值.
2.2.4 织物密度 采用Y511B型织物密度镜测量织物经纬密度.
2.2.5 织物面密度 按照GB/T4669—2008《纺织品机织物单位长度质量和单位面积质量的测定》进行测试.
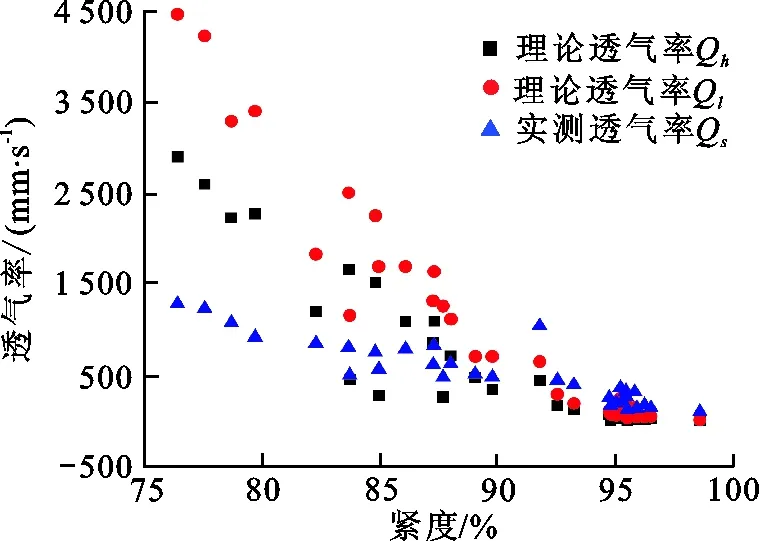
图 1 透气率与紧度之间的关系Fig.1 The relationship between air permeability and compactness
3 织物透气率预测方程构建
3.1 织物紧度与透气率相关性分析
织物紧度反映了织物的紧密程度,与织物密度及纱线直径有关.织物紧度与透气率之间的散点图如图1所示.织物紧度与透气量呈负相关,表明织物紧度越大,气体透过织物时的孔径越小,越不易透过.
将图1中的实验数据按织物紧度分为E<90%和E≥90%两部分,并对紧度与透气率进行线性拟合,如图2所示.
由图2可知,当紧度E<90%时,紧度E与理论透气率Qh、理论透气率Ql及实测透气率Qs的相关系数分别为0.773 0,0.876 8,0.762 2,对应的回归方程分别为Qh=16 602.59-182.39E,Ql=24 337.29-264.40E,Qs=5 308.48-53.87E,理论透气率Qh相较于理论透气率Ql更接近于实际透气率Qs.当紧度E≥90%时,紧度E与理论透气率Qh、理论透气率Ql及实测透气率Qs的相关系数分别为0.509 3,0.573 1,0.582 4,对应的回归方程分别为Qh=488 9.57-50.40E,Ql=7 375.33-75.87E,Qs=10 757.14-109.94E,理论透气率Ql相较于理论透气率Qh更接近于实际透气率Qs.

(a) 紧度<90% (b) 紧度≥90%图 2 透气率与紧度之间的相关性Fig.2 The correlation between air permeability and compactness
3.2 理论透气率与实测透气率相关性分析
当紧度E<90%时,对理论透气率Qh,Ql与实测透气率Qs进行线性拟合,如图3所示.由图3可知,理论透气率Qh与实测透气率Qs的相关系数为0.915 8,误差范围为7.72%~146.06%,平均误差为62.54%;理论透气率Ql与实测透气率Qs的相关系数为0.877 5,误差范围为37.81%~268.33%,平均误差为153.54%.表明实测透气率Qs与理论透气率Qh之间的线性相关程度更加密切.

(a) Qs与Qh的相关性 (b) Qs与Ql的相关性图 3 E<90%时,实测透气率与理论透气率的相关性Fig.3 The correlation between measured and theoretical air permeability (E<90%)
当紧度E≥90%时,对理论透气率Qh,Ql与实测透气率Qs进行线性拟合,如图4所示.由图4可知,理论透气率Qh与实测透气率Qs的相关系数为0.973 5,误差范围为54.77%~93.97%,平均误差为75.20%;理论透气率Ql与实测透气率Qs的相关系数为0.974 2,误差范围为32.98%~87.07%,平均误差为54.48%.表明实测透气率Qs与理论透气率Ql之间的线性相关程度更加密切.
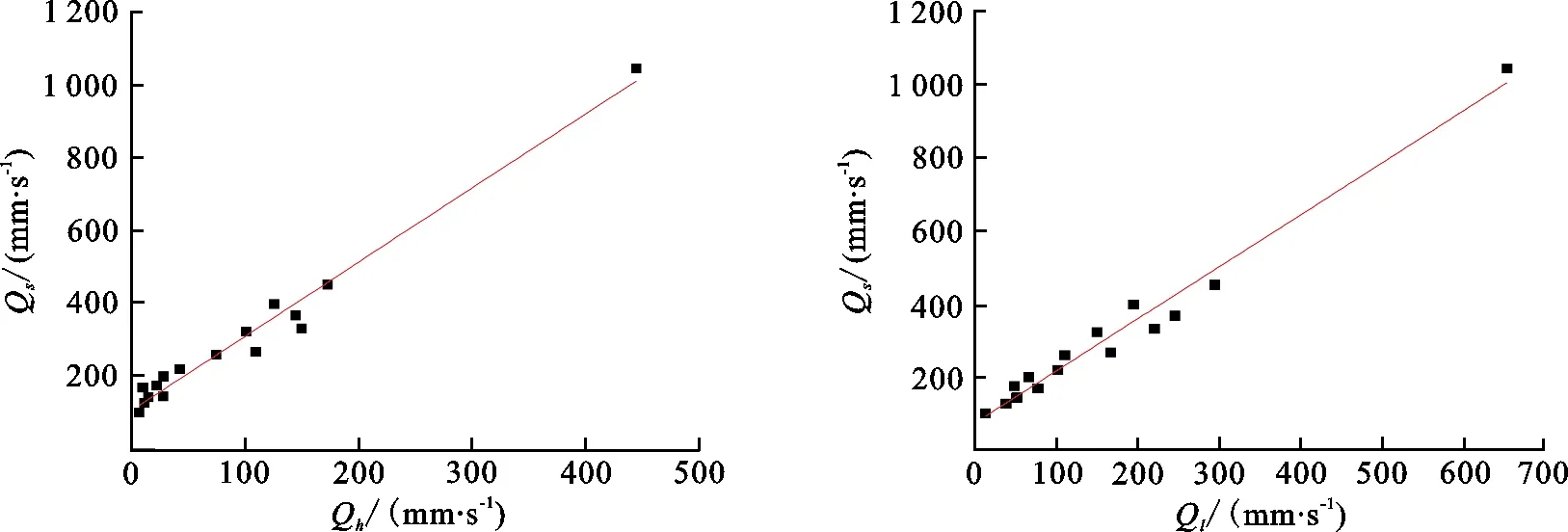
(a) Qs与Qh的相关性 (b) Qs与Ql的相关性图 4 E≥90%时,实测透气率与理论透气率的相关性Fig.4 The correlation between measured and theoretical air permeability (E≥90%)
3.3 织物透气率预测方程
在紧度E<90%,将实测透气率Qs作为目标函数,织物紧度E及理论透气率Qh作为自变量,进行回归分析,得到回归方程
Q=1 189.96-8.627E+0.248Qh.
(8)
相关系数R2=0.920 3,P=2.721×10-9<0.05.因此,可以认为该透气率回归方程在0.05水平下相关性显著.
在紧度E≥90%,将实测透气率Qs作为目标函数,织物紧度E及理论透气率Ql作为自变量,进行回归分析,得到回归方程
Q=584.43-5.289E+1.379Ql.
(9)
相关系数R2=0.974 8,P=8.473×10-13<0.05.因此,可以认为该透气率回归方程在0.05水平下相关性显著.
这是由于当织物紧度E<90%时,织物内孔隙尺寸相对较大,当气体透过织物时,在织物孔隙中部区域易于形成层流运动,因此,等速当量直径适用于低紧度下织物透气率的预测;当织物紧度E≥90%时,织物内孔隙尺寸相对较小,气体流经织物时受孔隙结构、纱线毛羽、几何结构相等因素影响,使得气体流经织物时产生涡流,形成紊流运动,因此,流量当量直径适用于高紧度下织物透气率的预测.
4 织物透气率预测方程验证
为了验证公式(8)及公式(9)的正确性,重新采集7种纯棉平纹织物试样进行验证,其结构参数及计算值如表2所示.对预测透气率Q与实测透气率Qs进行线性拟合,结果如图5.

表 2 验证样参数
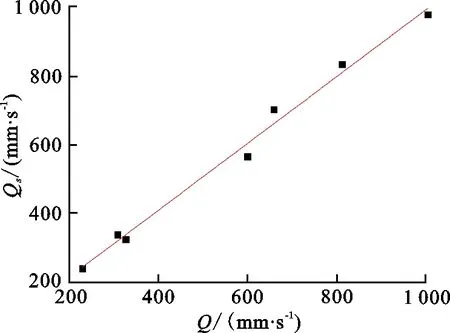
图 5 实测透气率与预测透气率的相关性Fig.5 The correlation between measured and predictive air permeability
由图5可看出,利用预测方程对纯棉平纹织物透气性有较好的预测精度,预测值与实测值之间的相关系数为0.988 4,误差范围为2.04%~7.73%,平均误差为4.29%.表明回归方程公式(8)及公式(9)对纯棉平纹织物基本适用,即织物的透气率可以由理论透气率与织物紧度进行预测.
5 结 论
(1) 织物紧度E<90%时,采用等速当量直径dh计算得到的理论透气率Qh与实测透气率Qs的线性相关程度较高.当紧度E≥90%时,采用流量当量直径dl计算得到的理论透气率Ql与实测透气率Qs的线性相关程度较高.
(2) 以织物紧度分段,所得透气率与理论透气率及紧度的回归方程,并重新采集试样验证该公式,其计算值与实测值之间相关系数达到0.988 4,表明该回归方程可用于预测纯棉平纹织物的透气率.

