基于自学习Pauta和Smooth的地下水位异常值检测和平滑处理方法
李丽敏,温宗周,王 真,董勋凯
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
近年来,地下水超采导致水位持续下降,且恢复缓慢,所以精确有效的智能水位监测不仅可以提高传统人工水位监测的准确性,还可以有序地保存历史数据,以便分析水位变化规律和未来趋势[1-3].
目前有诸多水位监测设备可用,其中比较常用的有压力式和浮球式,但一般都存在各自的问题,即在数据采集过程中,因各种因素导致采集的数据集中含有大量的异常值和冗余值,其中为异常值与正常数据相比偏大或偏小,与实际情况不符,异常原因可以归结为随机扰动和采集装置受环境影响较大[4].
北方工业大学的游加基于普通监测井监测出现的数据冗余问题,提出一种有效去除冗余数据的算法,该算法综合了有效带宽法、算术平均法、时间序列分析法、权重分配等方法的优点[5];周川辰等从水位监测装置本身出发,开展地下水位监测仪器质量检测技术研究与应用,对地下水位监测仪器进行实验室检测和模拟野外比测的测试与分析,达到掌握国内外地下水位监测仪器产品的水位测量准确度、稳定性、环境适应性、固态存储、数据传输和其他性能指标,以及野外实际应用条件下稳定性、可靠性的目的[6];潘博等针对目前地下水位监测方法中利用普通监测井监测带来的数据冗余问题,提出了一种新的水位监测算法.该算法综合了有效带宽法、算术平均法、时间序列分析法、权重分配等方法的优点,采用有效带宽法和算术平均法获得有效水位点和计算基准点,运用时间序列分析法建立了小时间段数据预测模型,并在此基础上修正预测模型,使用权重分配法获得了近似水位点[7].
综上,目前研究人员和设计人员使用的方法多为利用一段时间累积的数据的平均值来描述异常值,这些方法在一定程度上可以剔除异常值或冗余值,平滑水位曲线,但鲁棒性不高,原因在于一段时间内的数据与其他数据之间的差距较大.除此之外,上述算法都比较复杂,会增加时间复杂性,不利于实时平滑处理.因此,本文提出基于自学Pauta准则的异常值检测方法,同时采用平滑处理[8-16]方法对异常值进行校正.
1 自学习Pauta准则和平滑处理原理
为了能够将地下水位数据中的异常值进行处理,首先需要对所有数据进行奇异值检测,符合剔除条件的进行平滑处理,不符合的保留原值.
1.1 自学习Pauta准则
Pauta准则是为了检验样本数据的异常值而被提出的,用于判断粗差的Pauta准则,以标准值的99.7%的置信概率给出,以列极限的标准偏差的三倍为基础,任何超过该基础的误差,判断其不属于随机误差的范畴,并认为其属于严重错误的范畴,在这种情况下,产生该误差对应的采样值是不可取的,应该将其从测量数据中删除.假设一段时间内的样本数据集Xi,利用Pauta准则检测异常值的过程如下:

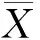

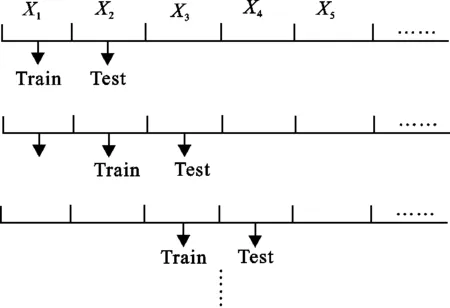
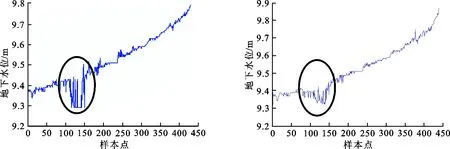
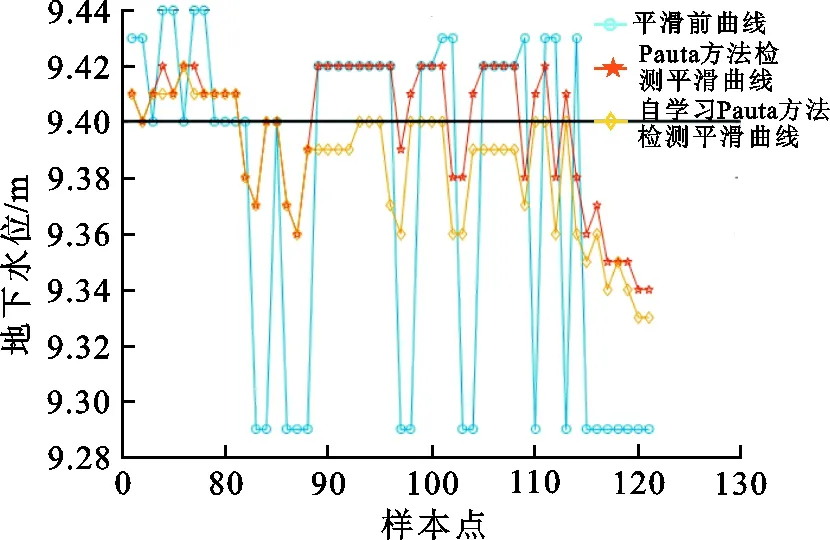
(4) 如果i 图 1 自学习Pauta准则奇异值检测过程Fig.1 Self-learning Pauta criterion value detection process 如图1所示,Train变量指向需进行均值和标准差计算的样本,在其之前的所有样本被用于计算均值和标准差,Test指向需被检测的样本,每检测到一个样本点,Train和Test整体向后移动1次,使得拉依达准则具有自学习功能,时刻将最新情况计算入均值和标准差,使检测结果更准确.具体算法过程如下: (4) 令Xi=Xi+1,如果i 在一般Pauta算法的基础上,增加了自学习环节,相当于每次对一个数据检测完之后,训练数据自动向后移动一位,提高了算法的可靠性. 当采用自学习Pauta准则算法检测出异常值时,通过平滑处理算法对其进行校正.假设xi(i=1,2,…,n1)是集合X中的元素,当xi+1被检测为奇异值时,用式(1)进行平滑处理. 表 1 Smooth函数的调用方法Table 1 Calling method of Smooth function序号调用格式备注 1Z=Smooth(Y,SPAN)指定窗宽值法 2Z=Smooth(Y)5点滑移平均法 3Z=Smooth(Y,SPAN,METHOD)指定平滑方法 注:Z为平滑处理后的测试数据;Y为测试样本;SPAN为窗宽值;METHOD为平滑方法xi+1=xi-5+xi-3+xi-1+xi+24. (1) 当xi+1被检测为正常值时,用式(2)来表示. xi+1=xi+1. (2) 式(1)采用四点平滑方法处理异常值,为了方便改变平滑曲线的点数,也可以通过MATLAB函数库中的Smooth函数来实现[18],利用该函数可以方便的实现点数的设置,从而同时调试该函数实现不同的平滑效果.如表1所示为Smooth函数的调用方法. 图 2 内蒙古某地采集的地下水位数据Fig.2 Groundwater level data in a certain area of Inner Mongolia 为验证自学习拉依达准则在奇异值检测中的作用,对其进行了仿真验证.利用地下水位监测装置对内蒙古某地的地下水位进行连续监测,从2015年10月10日到2015年12月22日每4 h采集一次,水位随时间变化如图2所示. 在本文中,将Pauta准则与自学习算法和平滑处理相结合用于地下水位异常值监测.为了展示这种算法的出色性能,测试了两种算法在准确性方面的性能.测试结果如图3和图4所示. 从图2可以看出,地下水的趋势随时间逐渐上升,在整个时间序列中,有很多异常样本数据,例如样本点70~300的样本数据,需要将这些异常样本数据进行平滑. 图3为采用一般Pauta算法和平滑算法进行奇异值检测和处理的结果,对比于图1未处理的原始数据,可以看出其中有很多奇异值已经被平滑处理掉了,效果较好.但仍然存在部分奇异值,如图3中被圈出部分.图4所示为其于自学习Pauta准则和平滑算法的奇异值剔除效果. 图4的曲线比图3更平滑,对用一般Pauta准则没有检测到的奇异值也进行了修正,说明使用自学习Pauta准则进行奇异值检测的算法是有效的. 对70~120采样点平滑前后数据进行对比,结果如图5所示.从数据分布来看,第82,83个和第85,86,87个数据点采样数据为均9.29,其明显偏离数据的变化趋势曲线,其数据应该在9.40左右变化.由此说明这些数据为异常值.为了将其有效平滑,首先采用一般Pauta准则对其进行检测并用平滑算法进行数据处理,为了提升效果,应用自学习Pauta算法进行数据处理. 图 3 基于Pauta准则的奇异值 图 4 基于自学习Pauta准则和平滑算法 剔除效果 的奇异值剔除效果 Fig.3 Singular value culling effect based Fig.4 Singular value culling effect based on self- on Pauta criterion learning Pauta crrterion and Smooth algorithin 图 5 70~120点数据经过一般Pauta算法和 自学习Pauta算法进行检测效果比较Fig.5 Comparison of detection effect of 70~120 point data by general Pauta algorithm and self-learning Pauta algorithm 从图5可以看出,采用自学习Pauta方法比一般Pauta方法更有效剔除奇异值.同年同时期该地区的地下水位的平均值为9.4 m,所以测试时以9.4 m为目标值,以平滑前、Pauta方法检测平滑和自学习Pauta方法检测平滑后的数据为验证数据,利用式(3)计算其方差 (3) 平滑前,采用Pauta方法检测平滑后以及采用自学习Pauta方法检测平滑后的方差计算结果分别为0.004 6,7.745 1×10-4,6.254 9×10-4.可以看出,自学习方法与其他方法比较,方差最小,性能更优,有效解决了地下水位异常值的问题. 提出基于自学习Pauta准则和平滑处理算法的地下水位异常值检测和校正方法,从工程实践中收集源数据,即以内蒙古某地监测的水位数据作为本文的测试数据来源,对本文算法进行了性能测试,测试结果表明该算法是有效的,解决了一般Pauta算法检测效果偏差的问题,对提升地下水水位监测水平提供了算法的依据.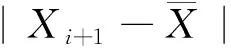

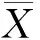

1.2 平滑处理算法


2 仿真验证
3 结束语

