正弦定理(第二课时)西蒙数学认知工作单设计

广东省华南师范大学数学科学学院(510631) 曾庆煜

基于西蒙数学教学理论,考虑到学生在正弦定理的第一课时中已经经历了以“直角三角形——锐角三角形——钝角三角形”的探索过程和用作高法证明正弦定理,即在一个三角形中,各边和它所对角的正弦的比相等的过程,本认知工作单基于学生的认知基础精心设计认知起点,采用小步教学,编排题组,突出小结等方式来展开“升级版”正弦定理,即三角形的各边和它所对角的正弦的比值相等,并且该比值等于该三角形外接圆的直径的探索、证明与应用,便于学生自我学习.

一、学习目标

1.探索与证明三角形的各边和它所对角的正弦的比值的几何意义——该三角形外接圆的直径;

2.理解“升级版”正弦定理的结构不变性和表达这一定理所用字母的可变性;

3.会用“升级版”正弦定理达到化边为角,化角为边的目的;

4.经历探索和证明“升级版”正弦定理的过程,领悟分类讨论思想和化归思想,学习由特殊到一般,由一般到特殊的思维方法,培养逻辑推理素养;

5.欣赏“升级版”正弦定理的对称美、概括性,领悟其中所蕴含的变与不变的辩证关系,为数学所震撼,增强学好数学的信心.

(注:本认知工作单所用名词“升级版”正弦定理并非规范数学用语,但它容易让学生区分第一课时所学的正弦定理,使语言表达更为简洁.为了引起学生的注意,本认知工作单在提出“升级版”正弦定理时给予相关说明.)

二、知识建构

试一试探索三角形的各边和它所对角的正弦的比值的几何意义

图1

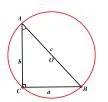
图2

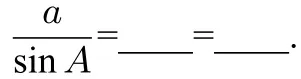
(2)(看一看)借助几何画板软件来构造许多锐角三角形和钝角三角形,请观察在这些三角形中边a和它所对角的正弦的比与对应三角形外接圆的直径的关系(如图3所示).

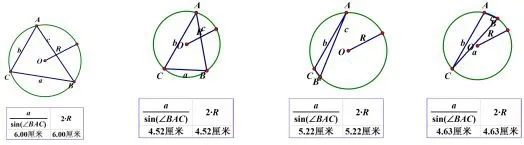
图3

小结:1.各边,它所对角的正弦,直径;

试一试命题证明

1.分析

此证明题的题设是___,结论是___.结论与我们所学的关于三角形边角关系的____定理的结论相似,以此来简化结论.题设有___三角形、__三角形两类.于是考虑对简化后的命题分成____种情况讨论.结合所得到的直角三角形已有的结论,能否考虑引入辅助元素将___三角形、___三角形的问题转化为直角三角形的问题呢?

2.证明过程

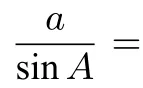
图4

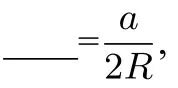
(2)在钝角△ABC中.

(提示:①构造一条直角边为a,其对角的正弦与角A的正弦相等,斜边为外接圆的直径的直角三角形;②若A,B∈(0,π),sinA=sinB⇔A=B或A+B=π.)

综上所述,原命题得证.

2. 正弦;(1)BO(或OB),D,CD(或DC),BD(或DB),∠BCD(B与D可以交顺序),△BCD(字母顺序可不同),sinD,D,sinD;

图5

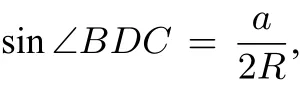
三、学习迁移

做一做题组一:“升级版”正弦定理的内涵

1.在△DEF中,三边为m,p,q,它们的对角分别为D,F,E,△DEF的外接圆半径为r,且p=3,E=45°,F=30°,则r=____.

2.已知AB是⊙O的直径,C是⊙O上一点,CM切⊙O于点C,弦CD交AB于E,过点E作CM的垂线,垂足为F,求证:AB·EF=CE·CD.

3.在⊙O中,弦AB,CD相交于M,且AB⊥CD,求证:AM2+BM2+CM2+DM2等于定值.

答案:1.6;

2.提示:连接AC,AD,运用弦切角定理、正弦的定义、正弦定理获得等量关系,进而求证.

3.提示:连接AC,AD,BD,在△ABD和△ACD中分别运用正弦定理用R表示BD,AC,再运用两次勾股定理可证.

小结:“升级版”正弦,边角三角形外接圆的直径,三角形.

做一做题组二:边角互化

2.若b=asinC,c=acosB,判断△ABC的形状.

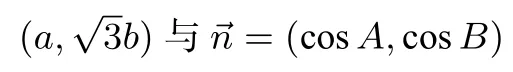
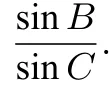
答案:1.等边;

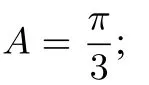
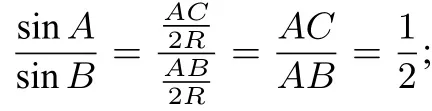
四、能力拓展

2.已知⊙O1与⊙O2相交于A,B,⊙O1与⊙O2的半径分别为r1,r2(定值),过A点如何引割线CAD,方可使S△BCD最大?

3.在△ABC中,若 (a2+b2)sin(A-B)=(a2-b2)sin(A+B),判断△ABC的形状.

(1)求sinBsinC;

(2)若 6cosBcosC=1,a=3,求bc.

五、总结与反思

1.本堂课要掌握哪些基本知识与基本技能?

2.本堂课学会了哪些数学思想与数学方法?