推广的常息力延迟索赔风险模型的破产概率
金燕生, 侯文婷
(燕山大学 理学院 河北 秦皇岛 066004)
0 引言
重大疾病或重大交通事故的发生常常伴随着巨大的财产损失. 基于此,保险公司设计了重疾险和第三方保险,承诺在首次出险后一段时间内再次出险仍将进行二次赔付. 风险模型中,首次赔付和二次赔付分别称为主索赔和延迟索赔,通常认为其分布是重尾的[1-2]. 重尾分布下带常数利息力的风险模型不仅刻画了造成保险公司破产的大额索赔,而且还反映了盈余资本在常数利息下的累积[3-4]. 针对此模型,文献[5]研究了索赔额属于L∩D族且负相依下的有限时破产概率. 文献[6]在索赔额属于C族且上尾渐近独立情形下得到了破产概率渐近表达式. 文献[7]给出了索赔到达间隔由独立变为WLOD(宽下象限相依)情形下的有限时和终极破产概率. 文献[8-10]则将保费推广为随机过程,给出了相应的有限时破产概率. 文献[11]又将延迟索赔增加到模型中,但保费仍为常数,在索赔到达为Poisson过程条件下,得到了新的破产概率等价式. 文献[12]将文献[11]中索赔额由独立变为负相依,索赔到达推广为更新过程,但索赔额分布缩小到L∩D族.本文继续考虑带有延迟索赔的风险模型,将索赔额扩展到广义负相依,又将保费总收入推广为非负非降的随机过程,在索赔到达为更新过程的情形下,得到了有限时破产概率的渐近等价式. 文中所建模型包含了保费收入为线性过程且索赔额负相依这一特殊情形,同时也更符合实际.
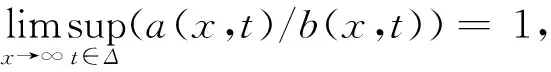
1 模型和引理
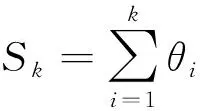
(1)
其中:{C(t),t≥0}表示到时刻t为止的保费总收入,满足C(0)=0,C(t)<∞;Xi和Yi分别表示第i次主索赔和延迟索赔;Wi表示相应的延迟时间间隔;IA表示集合A的示性函数.
通常定义有限时破产概率为
(2)
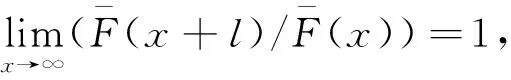
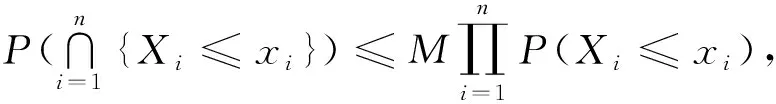
广义负相依不仅包含了负相依,而且还包含了某些正相依序列,具有更广泛的研究价值[14].
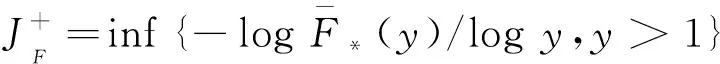
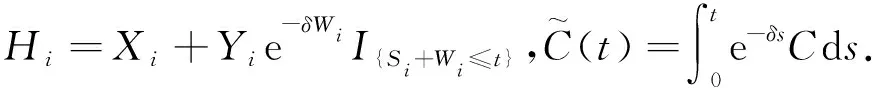
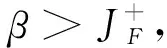
引理2[15]若{Xi,i≥1}是END,{gk,k≥1}均是非增或均是非降的,则{gk(xk),k≥1}仍是END.
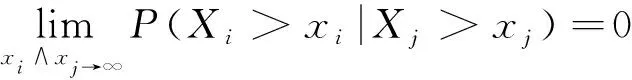
引理4在假设(A2),(A3)下,若F,G∈L∩D,则{Hi,i≥1}是END,且对∀i≥1有Hi∈L∩D.
证明因为{Xi,i≥1}和{Yi,i≥1}均为END,故由文献[17]的引理5可知,{Xi+YiI{Si+Wi≤t},i≥1}是END. 又对∀i≥1,P(0 引理5设任意非负随机变量Z与{Xi,i≥1},{Yi,i≥1},{Wi,i≥1},{N(t),t≥0}两两相互独立,在引理4条件下,对任意的T及正整数m0,有 (3) 证明对k=1,2,…,m0,由已知独立性条件有 P(Z∈dz)P(S1∈ds1,…,Sk+1∈dsk+1). (4) 取1≤i≠j≤k,由引理4知∃M>0,有P(Hie-δsi>x+z,Hje-δsj>x+z)≤MP(Hie-δsi>x+z)P(Hje-δsj>x+z)=o(P(H1e-δs1>x)).则 (5) (5)式中最后一步等价式可由L族定义得到.又对∀L>0,有 (6) 对于Δ1,再次利用L族性质有 (7) 对于Δ2,由D族定义,存在x0>0及常数c0,当x>x0时 (8) 定理1对于模型(1),在假设条件(A1)~(A3)下,若F,G∈L∩D,则有限时破产概率满足 (9) (10) 对I1,由引理5知,在Z≡0时,有 (11) 又由文献[14]知,对∀t∈[0,T],当m0→∞时,有(E((N(T))p+1)I{N(T)>m0})/λt→0.可得 (12) 从而由式(10)~(12)知ψ(x,T)P(H1e-δs>x)dλs.另一方面,对上述m0, (13) 类似I2证明方法,有J2≤P(H1>x)EN(T)I{N(T)>m0}.从而 (14) 上式第2个等价关系可由引理3得到. 从而定理得证. 与以往模型相比,本文考虑了延迟索赔的影响,并在保费随机,索赔额相依情形下得到了破产概率渐近等价式,该结果对保险公司在新的承保模式下进行风险管控具有一定的指导意义.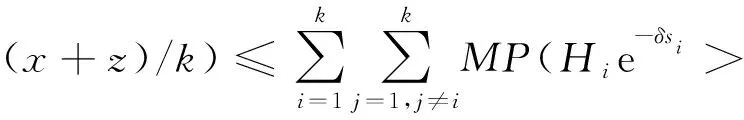
2 主要结果
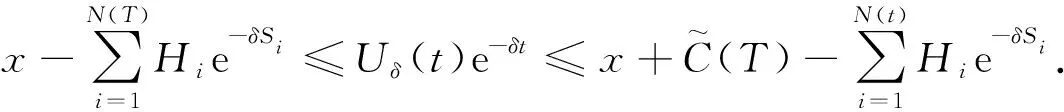
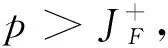

3 结论

