关于N(2,2,0)代数的广义交换性
邓方安
(陕西理工大学 数学与计算机科学学院, 陕西 汉中 723000)
许多学者使用代数工具对模糊逻辑进行了研究,给出模糊逻辑的代数抽象(如偏序集上的蕴涵代数),研究偏序集上蕴涵代数与其他代数结构(如MV-代数、Heyting代数)之间的关系,以及偏序集上蕴涵代数的滤子与其结构等。1996年,笔者在研究模糊蕴涵代数时,提出了一个与著名的Hilbert第十问题H10有关的、比DA重写系统更广泛的代数系统,称为N(2,2,0)代数[1]。并证明了:在一个N(2,2,0)代数(S,*,Δ,0)中,若*运算幂等,则(S,*,Δ,0)就是DA重写系统,此时N(2,2,0)代数的合一问题是不可判定的;若N(2,2,0)代数(S,*,Δ,0)关于Δ运算幂零,则(S,Δ,0)是一个结合的BCI-代数。后来,有学者相继研究了N(2,2,0)代数的中间幂等元[2]、中间单位[3]、理想与关联理想[4]、正则半群[5]、RC-半群[6]以及E-反演半群[7]等问题。本文主要讨论N(2,2,0)代数的交换性、广义交换性。
1 预备知识
定义1.1[1]设S是含常元0的集合。在S中定义两个二元运算*和Δ,若满足以下公理:∀x,y,z∈S,
(F1)x*(yΔz)=z*(x*y);
(F2) (xΔy)*z=y*(x*z);
(F3) 0*x=x;
则称(S,*,Δ,0)是一个N(2,2,0)代数。
定理1.1[1]在N(2,2,0)代数(S,*,Δ,0)中,∀x,y,z∈S,恒有下列等式成立:
(F4)x*y=yΔx;
(F5) (x*y)*z=x*(y*z), (xΔy)Δz=xΔ(yΔz);
(F6)x*(y*z)=y*(x*z), (xΔy)Δz=(xΔz)Δy。
推论1.2[1]若(S,*,Δ,0)是一个N(2,2,0)代数,则(S,*,0)和(S,Δ,0)都是半群。
2 主要结果
定义2.1[8]设S是一个半群,∀(a,b)∈S×S,如果存在一个元素u∈S,使得ab=bau,则称S是一个R-交换半群。
定义2.2[8]一个半群S,∀(a,b)∈S,如果有ab=ba成立,则必有
axb=bxa, ∀x∈S
成立,则称S为条件交换半群。
定义2.3[9]如果一个半群S既是R-交换半群,又是条件交换半群,则称S是RC-交换半群。
定义2.4[9]设S是一个半群,∀(x,y)∈S×S,如果满足x2yx=xyx2,则称S是一个广义条件交换半群(简记GC-交换半群)。
定义2.5[10]设S是一个半群,对任意一对(x,y)∈S×S和每一个正整数n,如果有一个正整数m,使得(xy)n+m=xnyn(xy)m=(xy)mxnyn,则称S是一个弱指数半群。
定理2.1 在N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)中,如果∀a∈S,有a*a=0成立,则半群(S,*,0)是一个R-交换半群。
证明由假设,在半群(S,*,0)中,∀a∈S,有a*a=0,则

且由F6易得,∀a,b∈S,有
a*b=a*(b*0)=b*(a*0)=b*a,
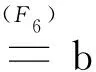
同理可得:此种情况下(S,Δ,0)也是一个R-交换半群。
定理2.2N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)和(S,Δ,0)都是条件交换半群。
证明∀a,b,x∈S,若有a*b=b*a成立,则有
x*(a*b)=x*(b*a)⟹a*(x*b)=b*(x*a)⟹a*x*b=b*x*a,
因此(S,*)是一个条件交换半群。
由定理2.1和定理2.2及定义2.3得到如下结论:
定理2.3 在N(2,2,0)代数(S,*,Δ,0)的每一个半群(S,*,0)中,如果∀a∈S,有a*a=0成立,则半群(S,*,0)是一个RC-交换半群。
定理2.4N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)都是广义条件交换半群。
证明由定理1.1知在半群(S,*,0)中,∀x,y,z∈S有
x*(y*z)=y*(x*z)
成立,于是∀(x,y)∈S×S,有x2*y*x=x*x*y*x=x*y*x*x=x*y*x2成立,因此(S,*,0)是一个广义条件交换半群。
定理2.5 在N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)中,∀(x,y)∈S×S和任意正整数m,n有:
(1)xn*y*x=x*y*xn;
(2) (x*y)m*xn*yn=xn*yn(x*y)m。
定理2.6[8]一个GC-交换半群S是一个弱指数广义交换半群,当且仅当对任意一对(x,y)∈S×S,存在一个正整数m,使得(xy)m+2=x2y2(xy)m。
定理2.7N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)一定是弱指数广义交换半群。
证明由N(2,2,0)代数的性质知,对任意一对(x,y)∈S×S和任意正整数m都有
(x*y)m+2= (x*y)2*(x*y)m=(x*y*x*y)*(x*y)m=
(x*x*y*y)*(x*y)m=x2*y2*(x*y)m,
因此,N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)一定是弱指数广义交换半群。
定义2.6[9]一个半群S,∀a,b,x,y∈S,如果满足等式:
(1)axyb=ayxb,称为中间半群;
(2)axy=ayx,称为右交换半群;
(3)xya=yxa,称为左交换半群。
容易验证下列两个定理成立。
定理2.8N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)和(S,Δ,0)都是中间半群,且(S,*,0)是左交换半群,而(S,Δ,0)是右交换半群。
定理2.9 在N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)和(S,Δ,0)中分别有下列等式成立:
(1) (a*b)n=an*bn;
(2) (aΔb)n=anΔbn。
定理2.10 在N(2,2,0)代数(S,*,Δ,0)中,下列条件等价:
(1)x*0=x,∀x∈S;
(2)x*y=y*x,∀x,y∈S。
证明(1)⟹(2):x*y=x*(y*0)=y*(x*0)=y*x;
(2)⟹(1):x*0=0*x=x。
注:一个N(2,2,0)代数(S,*,Δ,0),若满足∀x∈S,x*0=x,则(S,*,0)是交换半群,此时*与Δ运算相同,N(2,2,0)代数(S,*,Δ,0)退化为一个交换幺半群,0是一个幺元。
定理2.11 在N(2,2,0)代数(S,*,Δ,0)中,若*运算具有幂零性,则下列条件等价:
(1)x*0=x,∀x∈S;
(2)x*y=0⟹x=y,∀x,y∈S;
(3)x*y=y*x,∀x,y∈S。
证明(1)⟹(2):x=0*x=(x*y)*x=x*(y*x)=y*(x*x)=y*0=y;
(2)⟹(3):(x*y)*(y*x)=x*(y*(y*x))=x*((y*y)*x)=x*(0*x)=x*x=0,因此,x*y=y*x;
(3)⟹(1)由定理2.10可得。
定义2.7[10]在半群(S,*)中,一个元素a∈S,如果存在x,y∈S,使得x*a2*y=a,则称a是内正则元。如果S的所有元素都是内正则元,则称半群(S,*)是内正则半群。
定义2.8[10]一个正则且是R-交换半群称为正则R-交换半群。
定理2.12 若N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)是一个正则R-交换半群,则(S,*,0)也是内正则半群。
证明设(S,*,0)是一个正则R-交换半群,由正则性,则对于S的任意元素a∈S,存在x∈S,使得a=a*(x*a),再由R-交换性,则存在y∈S,使得
a=a*(x*a)=a*(a*x*y)=a2*x*y=x*a2*y,
于是(S,*,0)也是内正则半群。
3 结束语
本文主要讨论了N(2,2,0)代数半群的交换性和广义交换性,探讨了N(2,2,0)代数的正则R-交换半群与内正则半群的关系,指出了乘法运算具有幂零性的半群一定是交换半群、N(2,2,0)代数(S,*,Δ,0)的半群(S,*,0)和(S,Δ,0)都是条件交换半群等结论。而这种交换性及广义交换性在非经典逻辑中的应用将是我们后续研究的一个方向。

