基于Kriging近似模型的GCHE曲轴稳健性设计

付磊，张洪信，赵清海，徐东，王东

(青岛大学 a. 机电工程学院; b. 动力集成及储能系统工程技术中心，山东 青岛 266071)

0 引言

缸间齿轮联动液压发动机(gear-linked cylinders hydraulic engine，GCHE)是一种将燃料燃烧热能转化为流体压力能的新型动力装置，结构原理如图1所示。缸间通过齿轮齿条机构完成动力传输；曲轴飞轮组位于机体一侧，只有一个曲拐，该单侧曲柄连杆机构将柱塞往复运动转化成旋转运动，并控制活塞行程、驱动附属系统。曲轴和机体结构相对传统发动机大为简化。GCHE曲轴工况及受力与传统发动机明显不同，需要对其进行结构设计优化，以适应最佳工作状态。文献[1]对曲轴采用确定性方法实现优化，但计算量较大；文献[2] 对曲轴采用响应面近似模型不仅完成了对曲轴优化的目的，而且大大提高了计算效率，但未考虑稳健性提高约束的可靠度。本文将基于Kriging近似模型与最优拉丁超立方试验设计方法，创建面向6σ稳健性优化设计的曲轴结构尺寸优化模型，来完成曲轴结构优化。

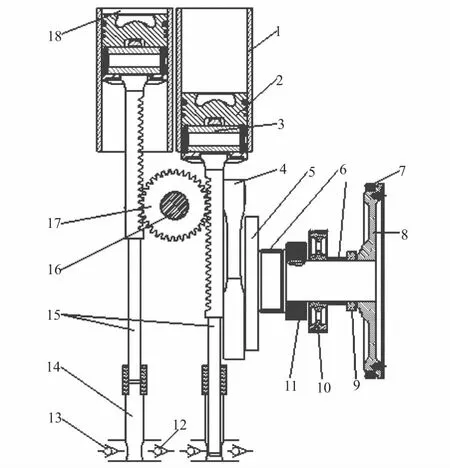
1—缸套；2—活塞；3—活塞销；4—连杆；5—曲轴；6—滑动轴承；7—启动齿圈；8—飞轮；9—密封圈；10—驱动带轮；11—正时主动齿轮；12—入口单向阀；13—出口单向阀；14—泵腔；15—柱塞；16—支撑；17—缸间齿轮；18—动力腔图1 两缸GCHE结构原理示意图

1 GCHE曲轴参数优化模型

将曲轴的主要的结构尺寸作为设计变量，将应力和变形作为优化的约束条件，目标函数为体积最小。对曲轴强度影响不大的结构进行简化后的参数化模型如图2所示，图中变量为设计变量。

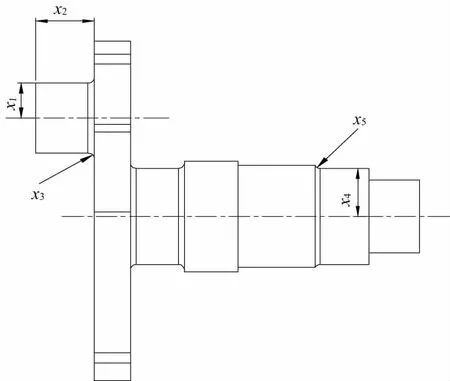
图2 曲轴参数化模型

1.1 设计变量

作为曲轴设计变量的选择需要满足以下的要求：对曲轴变形、质量、应力等具有较大的影响；能反映出曲轴结构外形的尺寸；曲轴工作时承受的应力比较复杂，根据传统发动机曲轴疲劳断裂失效经验，连杆轴颈与主轴颈过渡圆角半径应作为设计变量；尺寸之间相互独立，互不影响；对发动机整体的参数以及其他零件的主要尺寸没有影响；加工工艺性好，容易实现。综上所述，选定5个尺寸作为输入变量，其原始值及波动范围如表1所示。

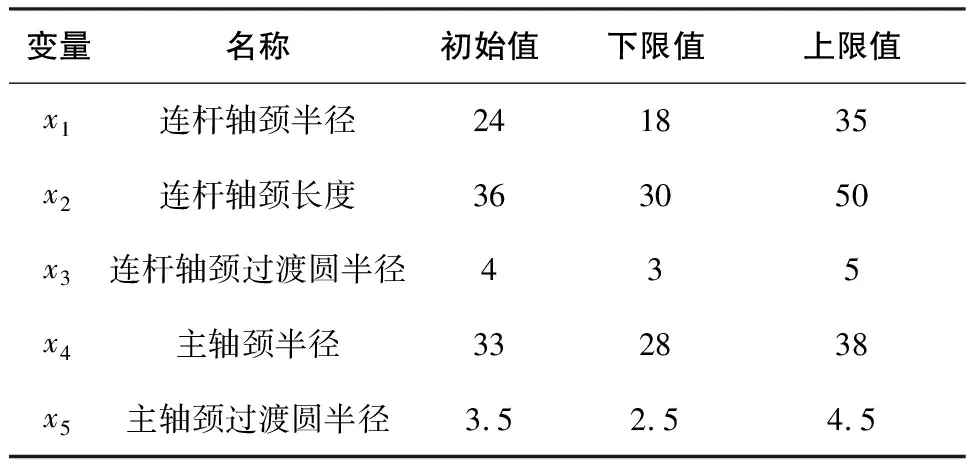
表1 曲轴初始设计变量及取值范围 mm

1.2 约束函数

为了防止由于交变载荷作用而使曲轴断裂失效的情况发生，设计曲轴应该保证其疲劳强度可以满足工作条件；为了尽可能减少主轴颈变形，保证相关的配合间隙，曲轴需要足够的刚度；此外还需要满足设计变量的上下限要求。

1) 疲劳应力约束

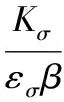
(1)

式中，Sσ为疲劳安全系数；σ-1为材料的疲劳应力极限；εσ为曲轴的结构尺寸影响系数；Kσ为弯曲在圆角处的应力集中的系数；β为强化系数；σm为平均应力；σα为应力幅；ψσ是应力循环不对称敏感系数。

ψσ=(2σ-1-σ0)/σ0

(2)

式中，σ0为脉动循环时材料的弯曲疲劳极限。

2) 变形约束

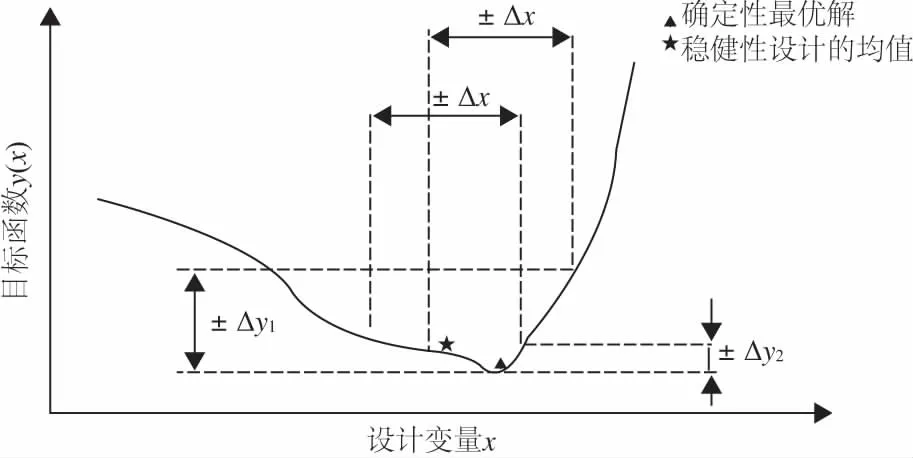
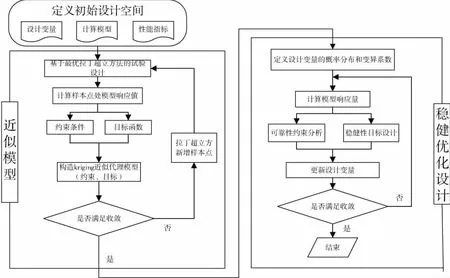
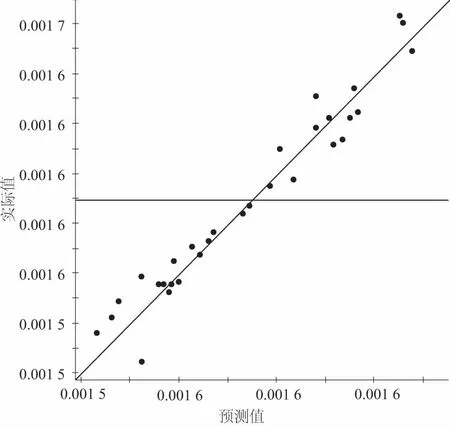
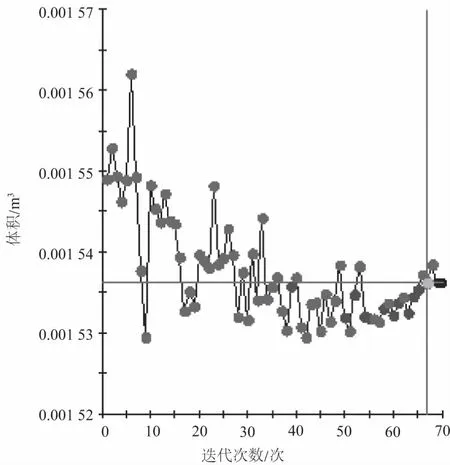
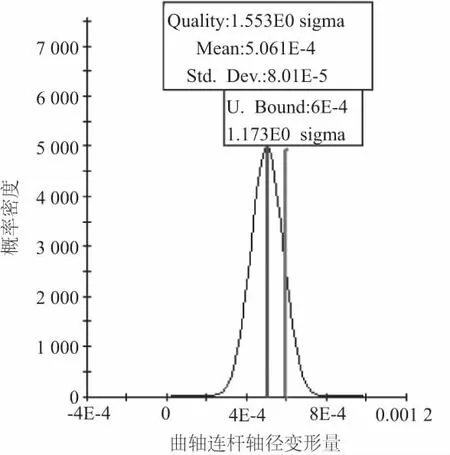
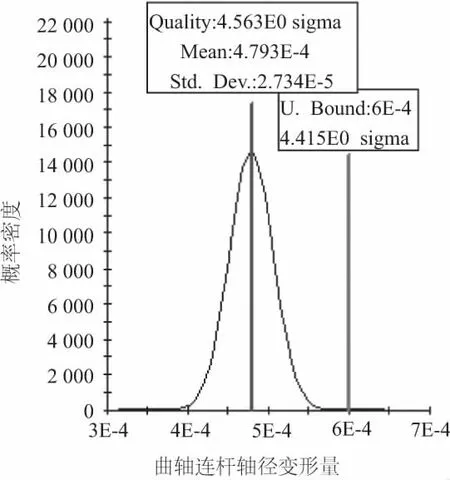
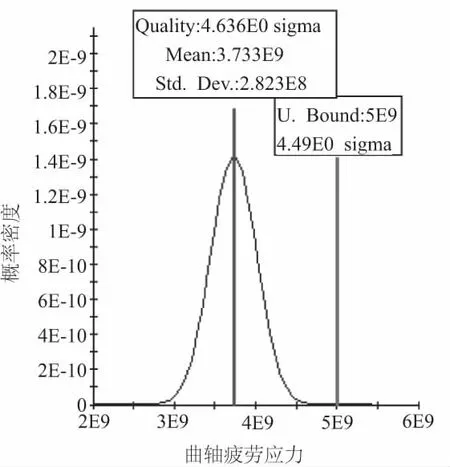
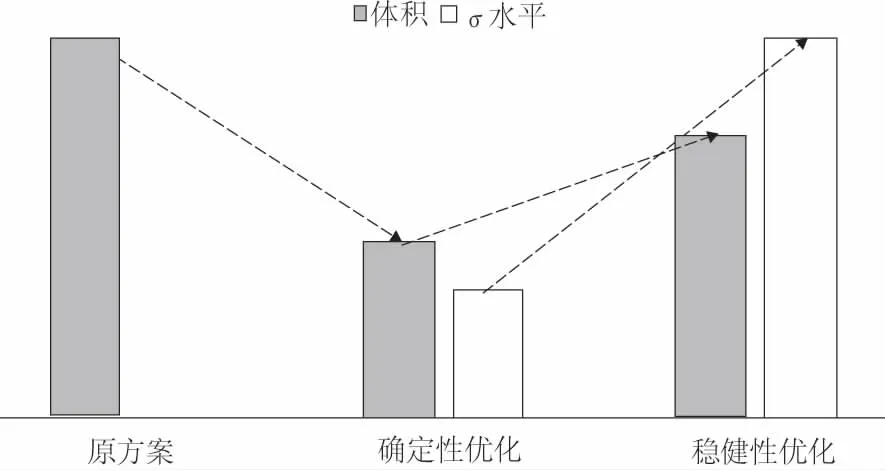
Δrmax

(3)

式中，Δrmax为连杆轴颈的最大变形量，T1是分析计算中的变动量。

1.3 优化模型

(4)

式中，目标函数V(Xc)为曲轴体积，设计变量Xc=[x1,x2,x3,x4,x5] 。约束条件包括疲劳强度σmax(Xc)，其最大值为5 000MPa；连杆轴颈刚度变形Δrmax(Xc)最大值为0.6mm。

2 6σ稳健性优化设计方法

稳健性是通过寻找目标函数变化中波动小的区域，避免由于变量的不确定性而产生响应的不稳定变化，而且还可以提高约束条件的可靠度。其优化原理见图3。从图中可知确定性最优结果在±Δx变化时，目标函数的响应范围Δy1波动较大，而稳健性的最优结果在±Δx变化时，目标函数波动Δy2较小。

图3 确定性与稳健性优化结果对比图

确定性与稳健性的优化数学模型公式分别如式(5)和式(6)所示。

(5)

(6)

式中，X随机设计变量集；F与H分别为目标函数和约束条件；±ΔX表示随机变量X的变化范围；XL和XU分别为设计变量X的上下限。

6σ稳健性优化是一种可以同时完成稳健性要求和可靠度要求的设计方法，其数学模型可表示为：

(7)

式中n表示σ水平。

根据稳定性优化的原理，将实验设计、近似模型与6σ稳健优化技术相结合，具体流程如图4所示。

图4 优化流程图

3 基于近似模型的确定性优化

3.1 近似模型的构建

常用的近似模型:响应面方法、径向基神经网络和Kriging模型等[3]。本文所采用的Kriging模型在研究高度非线性的对象时，相比其他的方法的预测效果相对较好。Kriging模型是由相关模型与回归模型两部分构成，因此具有较高的精度。回归模型包含了零阶、一阶与二阶多项式拟合。相关模型包括指数、线性、高斯等函数。

假设n维的设计变量S=(s1s2…sn)T，响应值为Y=(y1y2…yn)T，基于近似模型的响应值可表示为：

Y=βF(s)+z(s)

(8)

式中，F(s)为全局回归模型，β为回归系数，z(s)为相关函数，服从是在回归模型的基础上创建的均值为零，但方差不为零的局部偏差。

对于任意两个z(si)和z(sj)之间的协方差为:

Cov[z(si),z(sj)]=σ2r(si,sj)

(9)

为了提高近似模型的模拟精度，实验设计采用最优拉丁超方的实验设计(optimal latin hypercube design, Opt LHD)。在实验设计的基础上，选取kriging模型作为优化模型，其中，拟合曲线的均方根值R2越接近于1，则近似模型越接近于真实模型，由结果分析计算可得，体积均方根值为0.948 22，其拟合效果如图5所示。

图5 曲轴体积拟合效果图

3.2 确定性优化

在近似模型的基础上，采用直接搜索算法(direct search)中的下山单纯形法(downhill simplex，DS)算法，进行结构优化设计。

优化过程经过66次迭代，最终求得在约束条件下最小的体积为1.51×10-3(m3)，与初始体积1.56×10-3(m3)相比减少3.8%，其体积变化如图6所示。

图6 确定性优化曲轴体积变化

4 基于6σ的稳健性优化

4.1 可靠性分析

采用可靠性评价(reliability analysis)来考察基于近似模型的确定性优化方案的质量水平。经过质量分析可知曲轴连杆轴径变形量与曲轴疲劳应力的可靠度分别为87.96%和95.89%，不满足可靠度>99.999%(即不满足4.5σ质量水平) ，因此确定性方案的可靠度较低，方案具有一定的局限性，需要进行稳健性优化设计。

4.2 6σ稳健性优化

根据稳健性数学模型公式(7)，构建曲轴的稳健性优化数学模型：

(10)

式中,n代表σ质量水平；VOL代表曲轴的总体积；G、F分别代表连杆轴径变形量与曲轴疲劳应力；GL、FL为G、F的设计上限(常数)。

通过6σ稳健性优化，设定曲轴约束达到4.5σ质量水平，即结果不满足设计的概率应低于0.001%。稳健性优化采用Kriging近似模型与下山单纯形法(downhill simplex，DS)算法。

通过稳健性优化，曲轴体积优化结果为1.536×10-3(m3)，比确定性优化设计增加0.026 m3，但比初始体积减少1.61%，达到轻量化效果，其体积变化如图7所示。

图7 稳健性优化曲轴体积变化

相比确定性优化，稳健性优化后约束条件质量水平均高于4.5σ。稳健性优化之前曲轴连杆轴径变形量的质量水平为1.55σ，经过优化后，其质量水平提高到4.56σ，如图8所示。同样曲轴疲劳应力质量水平由2.04σ提高到4.64σ，结构设计方案具有稳健性，如图9所示。

图8 稳健优化前后曲轴连杆轴径变形量σ质量水平对比

图9 稳健优化前后曲轴疲劳应力σ质量水平对比

由计算结果可知，稳健设计在满足约束条件的前提下，虽然体积较确定性优化有所增加，但各个约束条件的可靠度明显提高，在满足轻量化的基础上实现结构稳健性，确定性优化与稳健性设计对比如图10所示。

图10 各种方案优化结果对比图

5 结语

以GCHE曲轴为研究对象，结合实验设计、kriging近似模型技术与6σ稳健性优化，开展曲轴结构稳健设计，在保证满足约束的条件下，既使体积减少了1.61%，并且通过稳健性优化提高了约束的可靠度。结果表明，通过近似模型可在保证计算精度的前提下，有效地减少计算工作量。并且稳健设计能有效的降低产品的失效概率，提高结构的稳健性，具有一定的工程实用性和价值。