薄壁轴压方管极限承载力数值模拟与试验研究

何帆，肖瑛，田常录

(1. 江南大学 机械工程学院，江苏 无锡 214122； 2. 常德供电公司，湖南 常德 415000)

0 引言

薄壁型方钢管构件具有许多良好的结构性能，近年来，冷弯薄壁型钢结构在我国的住宅、办公楼、超市等结构厂房及各种大型设备中应用越来越广泛。因此对薄壁型方钢管构件承载能力的研究具有重要的意义。从20世纪80年代开始，对于箱形构件稳定性极限承载性能的研究工作就一直没有停止，国内外很多学者对箱形截面构件进行了理论推导和试验研究，近些年郭小农[1]、袁焕鑫[2]、刘海生[3]等国内知名学者分别就箱形截面的不锈钢、高强钢和Q235进行了相关试验研究或理论推导，但都只是针对某一类型的材料进行了研究，对不同材质下薄壁方管统一分析研究的文章还不多。

本文通过对Q235和不锈钢两个类型方管的加载试验，并结合翟希梅[4]，Ben Young[5]的试验结果得到了几种不同材质下薄壁方管极限承载力，将结果与通过ANSYS 数值计算得到的结果进行分析对比，并将试验结果与我国现行规范的有效宽度法和近年来新兴的直接强度法计算得到的极限承载力进行了对比。

1 试验概况与有限元分析

1.1 试验过程和模拟边界条件

试验选用油缸上置电液伺服万能试验机，型号为RE-8100，最大载荷为1 000 kN。试验采用固定端约束，一端用螺栓固定在试验机上，另一端和试验机上台坐接触。试验进行应变、位移与试件的破坏形态三部分的测试，在试件被破坏后记录试件的破坏特征及其极限载荷值。试验加载方式主要采用载荷控制，首先进行预加载，当测试系统上显示载荷大小为1 kN时，此时默认为初始状态，然后采用等速位移控制，加载速度为2 mm/min。用手动控制的方式，每加载20 kN记录一次数据。当出现载荷不变或者下降时，默认构件已经破坏，此时计算机会自动记录下最大载荷值。

在进行有限元分析的过程中，模型的边界条件应尽可能和试验的边界条件一致，因此本文采用固接的边界条件进行模拟分析。由于板单元自身的特点，仅需约束底面整个面的x、y、z方向的线位移即可实现完全固接，后续的数据对比分析也说明了模拟边界条件的准确性。

1.2 有限元分析

研究对象为一端轴向固定，一端完全固定的受压构件，截面为矩形截面。采用ANSYS14.5中的三维四节点(每个节点包六个自由度)的四边形Shell单元。主要因为Shell单元既能很好地模拟整体失稳和局部失稳，又能用于进行非线性屈曲分析。建模的方法是在ANSYS中直接建立整体模型。由于模拟的是方管柱，网格划分的实现较为简单，仅需确定合适的网格尺寸即可。因此在保证计算精度足够的条件下,通过变化网格尺寸发现当选择柱宽度的1/10作为每一单元的尺度时可以获得比较满意的计算结果。表1和表2列出了所模拟的13种截面的几何尺寸及材料特性，它们来源于已有方管试验研究和本文的试验研究[4-5]。

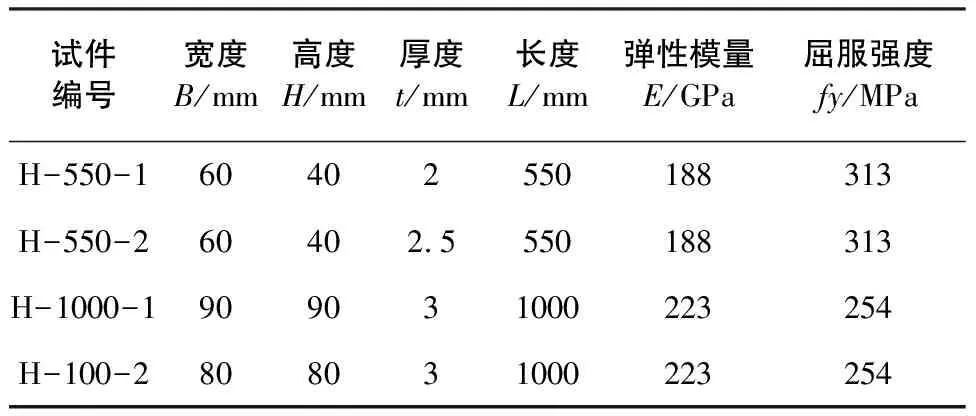
表1 本文试验构件几何尺寸及材料特性

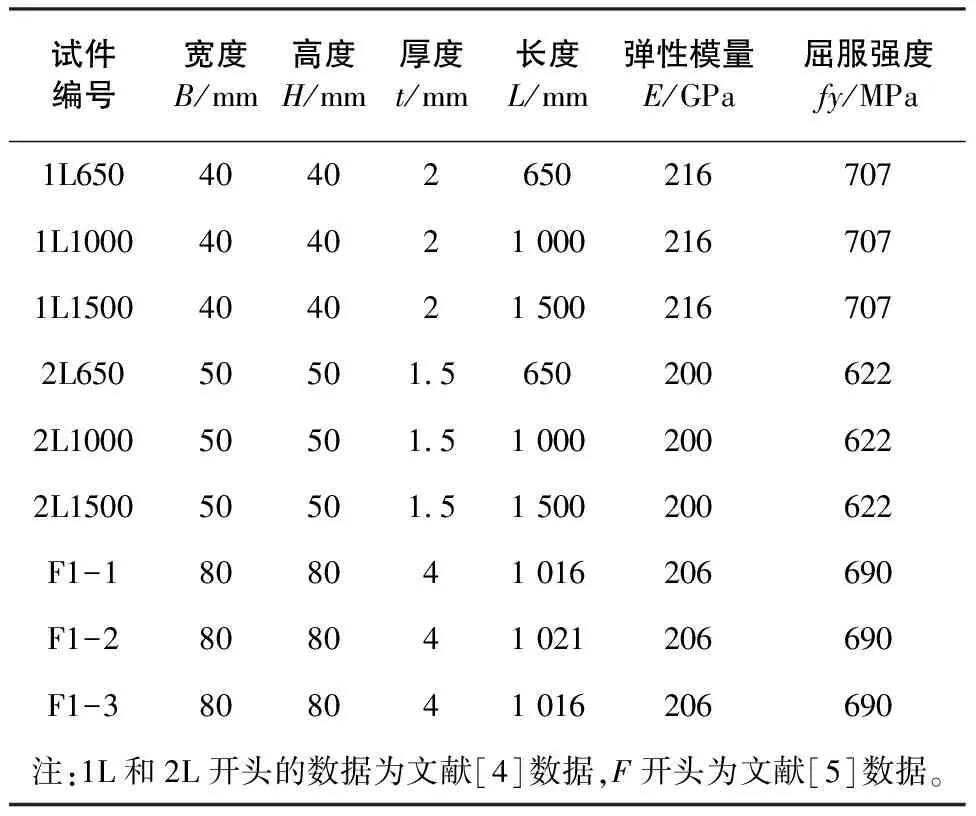
表2 文献[4]和文献[5]试验构件几何尺寸及材料特性

1.3 试验和数值分析

在利用非线性屈曲分析求解构件的极限承载力时，构件几何缺陷的影响不能忽略，在进行非线性屈曲分析之前，先进行特征值屈曲分析，然后取其一阶变形图作为非线性分析的初始缺陷。根据研究结果[6]，选取构件初始几何缺陷最大值为L/1 000。

在分析过程中材料属性定义为理想弹塑性材料，分析过程采用弧长法。相关研究表明，构件的长细比和宽厚比对构件的极限承载力都有较大的影响。因此，在进行有限元分析以及试验的过程中，要考虑构件长细比和宽厚比两个因素的影响。分析所得承载计算值与试验值的对比情况见表3。由表中可以看出，有限元分析所得极限承载力与试验结果吻合较好，除试件H-550-1外，其余计算结果与试验所得承载力之间的误差均在±8%以内。结果表明，采用L/1 000作为初始缺陷进行薄壁方管的极限承载力计算以及用ANSYS模拟的过程是比较准确的。

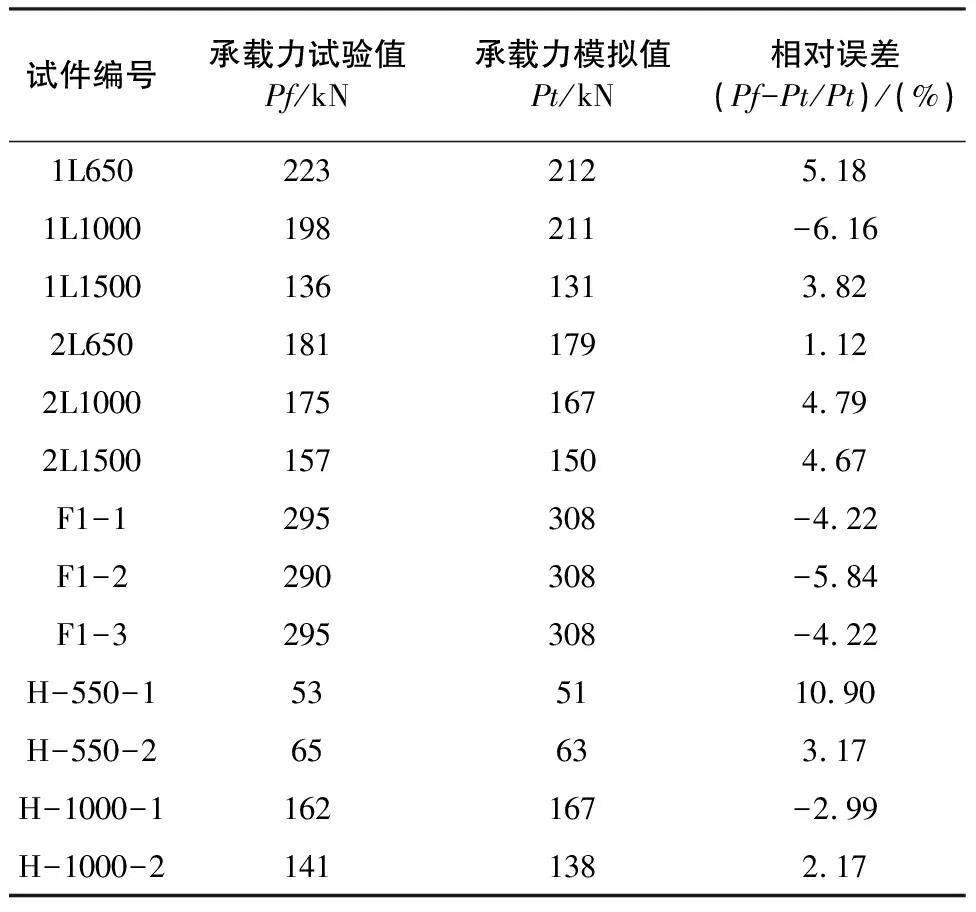
表3 ANSYS计算结果与试验结果的对比

图1给出了试验中H-550-1破坏形式的照片与ANSYS模拟破坏形式照片对比。试验结果和模拟结果均为局部失稳。

图1 试验中H-550-1破坏形式的照片与ANSYS模拟破坏形式照片对比

图2给出了试验中H-1000-1破坏形式的照片与ANSYS模拟破坏形式照片对比。试验结果和模拟结果均为整体失稳。

图2 试验中H-1000-1破坏形式的照片与ANSYS模拟破坏形式照片对比

2 有效宽度法和直接强度法计算短柱的极限承载力

2.1 有效宽度法

对于薄壁型钢构件的设计，我国主要是按照GB50018—2002《冷弯薄壁型钢结构技术规范》中的有效截面法。该方法在计算构件的承载力时用有效截面代替原截面以折减刚度，来考虑局部屈曲对整体稳定的影响。加筋板件、部分加筋板件和非加筋板件的有效宽厚比应按式(1)-式(3)计算[7]。

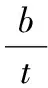
(1)

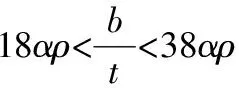
(2)

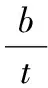
(3)

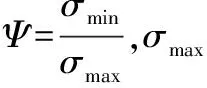
图3以板件的正则化宽厚比λn为横坐标，以承载力试验值和理论值的比值p/(ae·fy)为纵坐标，画出了有效宽度法设计计算曲线，并与试验结果进行了比较。

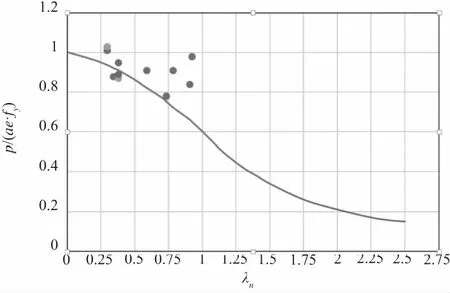
图3 试验结果与有效宽度法设计曲线对比

2.2 直接强度法

近年来，Schafer提出了一种新的计算轴压薄壁杆件的计算方法——直接强度法(简称DSM)，并且被纳入了北美规范AISI S100-2007中。对于轴心受压的方管，用直接强度法计算压杆的局部屈曲极限载荷Pnl的公式为[9]：

当λ1≤0.776时，

Pnl=Pne

(8)

当λ1>0.776时，

(9)

Pne=φAfy

(10)

其中；Pcrl为弹性局部屈曲时杆件压力，A为构件的横截面面积；fy为材料的弹性局部屈曲载荷；φ为压杆的稳定系数。

图4以板件的正则化长细比λc为横坐标，以承载力试验值和理论值的比值p/(ae·fy)为纵坐标，画出了有限宽度法设计计算曲线，并与试验结果进行了比较。

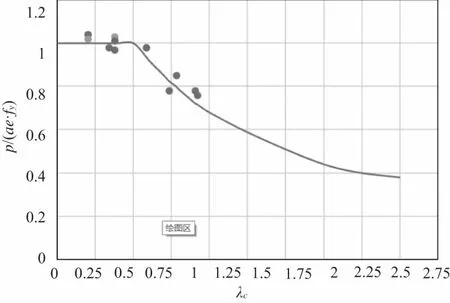
图4 试验结果与直接强度法设计曲线对比

2.3 结果分析

从图3中可以看出，有效宽度法在计算轴心受压立柱的极限载荷时，计算结果普遍低于试验值，结果相对趋于保守。从图4中可以看出，有效宽度法的计算结果和试验值比较接近，而且在相同条件下直接强度法更加简便适用，工作量明显低于有效宽度法。

3 结语

1) 建立了立柱的有限元数值模型，可以准确模拟方管的非线性材料力学性能、构件的局部与整体几何初始缺陷因素的影响。结果表明文中采用的有限元分析除试件H-550-1外，试验值与有限元模拟值相差在8%以内，说明该模拟是比较准确的。

2) 对于薄壁箱形截面有限宽度法的计算结果趋于保守，直接强度法的计算结果比较精确、简便适用，且计算工作量低于有效宽度法，在计算箱形截面构件承载力时更有优势。