基于主成分分析的高速铣削振动特性研究

林盖，林述温

(福州大学 机械工程及自动化学院,福建 福州 350108)

0 引言

随着现代社会对材料质量的需求越来越高，大量高精高效技术正快速发展。钛合金作为一种重要的结构金属，当采用高速加工时，还是高度依赖机床操作人员的技术和经验，难以预测加工表面质量。这是因为加工面的形成不仅与刀具的几何形状和切削参数有关，还与刀具和工件的振动特性有关[1-2]。刀具和工件的振动作为一种可通过相关设备实时监测的现象，有助于强化对表面质量的预测，所以高速铣削的振动特性引起了许多研究者的极大兴趣[3]。

高速铣削的振动特性已经进行了许多研究，但都着重于对振动特性的描述，很少研究振动特性对表面质量的影响[4-7]。这主要是因为振动信号形式多样，数据结构复杂，难以找出稳定且简单的振动特征量。因此，本文用统计学的一些方法，研究振动信号的特征。

功率谱密度(power spectral density，PSD)是具有综合分析意义的概率统计函数，从频域上考虑问题，研究随机振动各频率成分的功率分布情况。随机过程X(t)的功率谱密度为:

(1)

其中FX(ω,T)是XT(t)的傅里叶变换。

主成分分析(principal component analysis，PCA)就是利用降维的思想，将原有的多个指标转化为少数几个有代表性的综合指标，这些指标能反映原来指标的大部分信息(85%以上)，并且各个指标之间保持相互独立。

1 实验设备与实验方案

1.1 实验设备

实验采用5轴立式铣削加工中心MAZAK VARIAXIS 500-5XⅡ，其主电机功率为22.4 kW，最高转速达12 000 r/min。刀具选用直径为10 mm的涂层硬质合金立铣刀，材料为钨钢，齿数为4。实验工件材料为钛合金Ti6Al4V(TC4)，尺寸规格为100 mm×80 mm×20 mm。振动信号采集系统包括：振动信号采集仪器 LMS Test.Xpress及其配套软件、压电式传感器和计算机，以及Marsurf XCR20马尔粗糙度仪测量表面粗糙度。

1.2 实验方案

受实验条件所限，为保证实验数据充足，分别考虑5mm和10mm两组铣削宽度，选择L9(34)的正交表，设计两组正交实验，因素水平见表1。

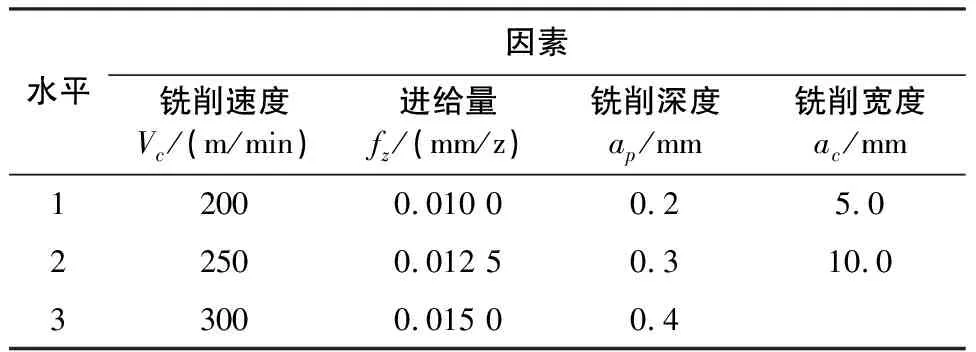
表1 实验因素水平表

实验过程中采用顺铣的方式加工工件。由于刀具和工件之间的相对振动难以直接测量，且主要考虑铣削过程中铣削力周期变化引起的自激振动和刀具断续切削等复杂切削机理引起的强迫振动[3]，因此选择将测点布置在刀具和工件的临近部位。在主轴和工作台的x、y、z3个方向上布置加速度传感器，测量该部位的加速度振动信号。x表示铣削进给运动方向，y表示铣削宽度方向，z表示铣削深度方向。具体实验环境如图1。

图1 传感器布置及铣削中心坐标轴示意图

2 实验数据处理与分析

2.1 实验数据处理

在实验过程中，用LMS振动信号采集系统测量每组实验3次走刀的加速度振动信号，并对振动信号做功率谱分析，部分实验结果见图2、图3。用马尔粗糙度仪测量每次走刀形成表面的表面粗糙度值，每刀测量3次，最后取9次的平均值。表面粗糙度测量结果见表2。

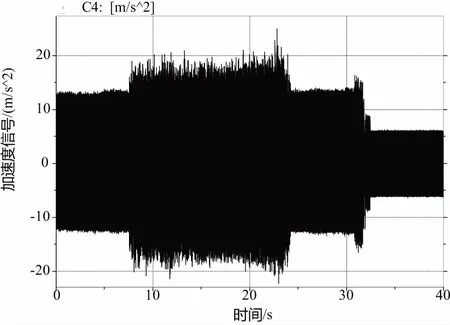
图2 加速度振动信号

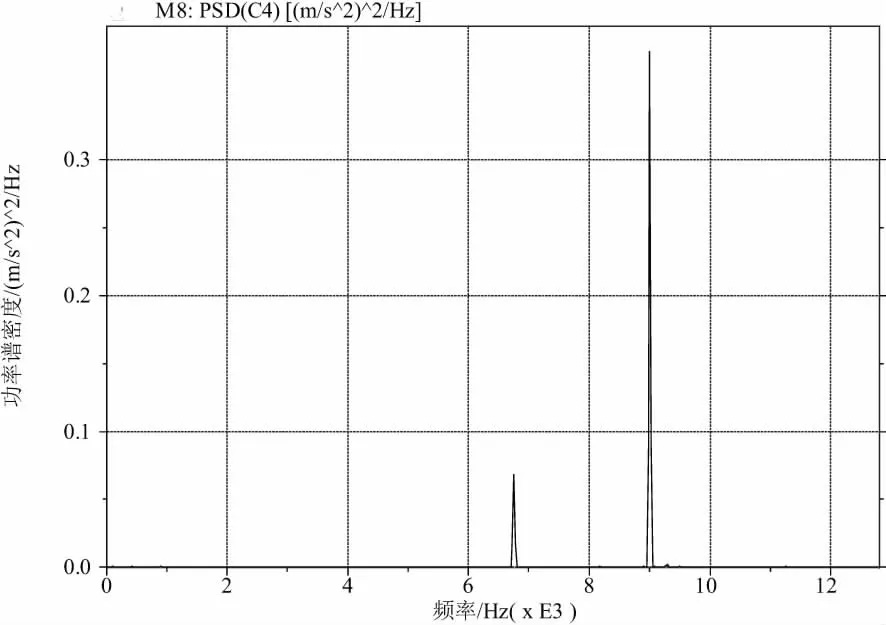
图3 加速度振动信号的功率谱密度

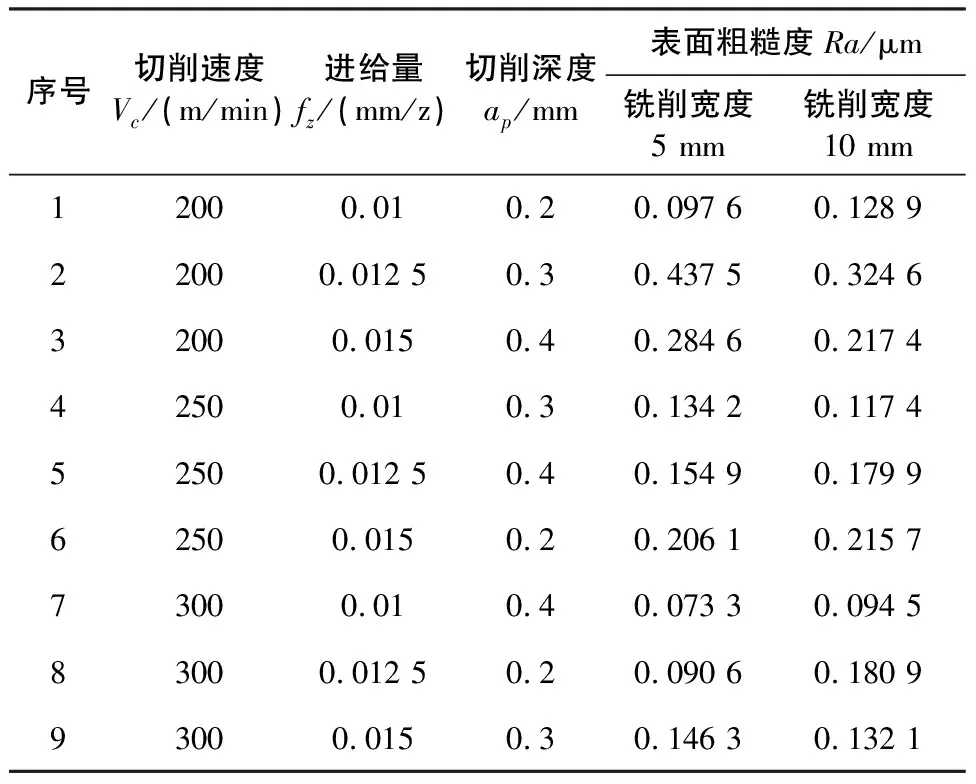
表2 正交实验方案下的表面粗糙度值

2.2 实验数据分析

在分别对主轴和工作台x、y、z3个方向上的振动信号做功率谱分析后发现，振动信号频率分布基本一致，主要集中在2个高频成分6 760Hz和9 000Hz，只有极少数存在微小偏差，低频成分所占比例极小，可以忽略不计。所以从6 760Hz和9 000Hz 2个频率成分的功率谱幅值研究高频振动对表面粗糙度的影响。

首先分析频率为6 760Hz的功率谱幅值对表面粗糙度的影响规律，18组实验数据如表3所示。

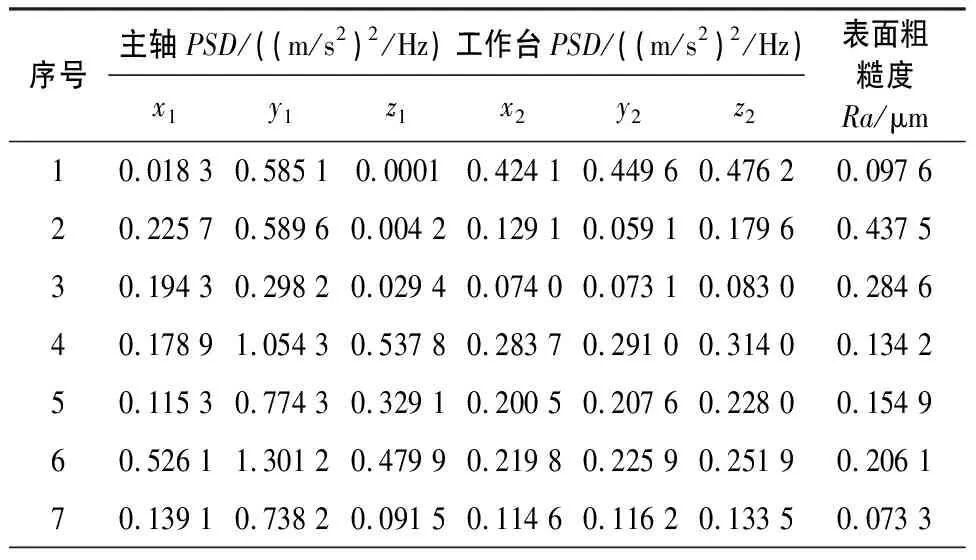
表3 主轴和工作台3个方向上的振动信号频率6 760 HZ处的功率谱幅值

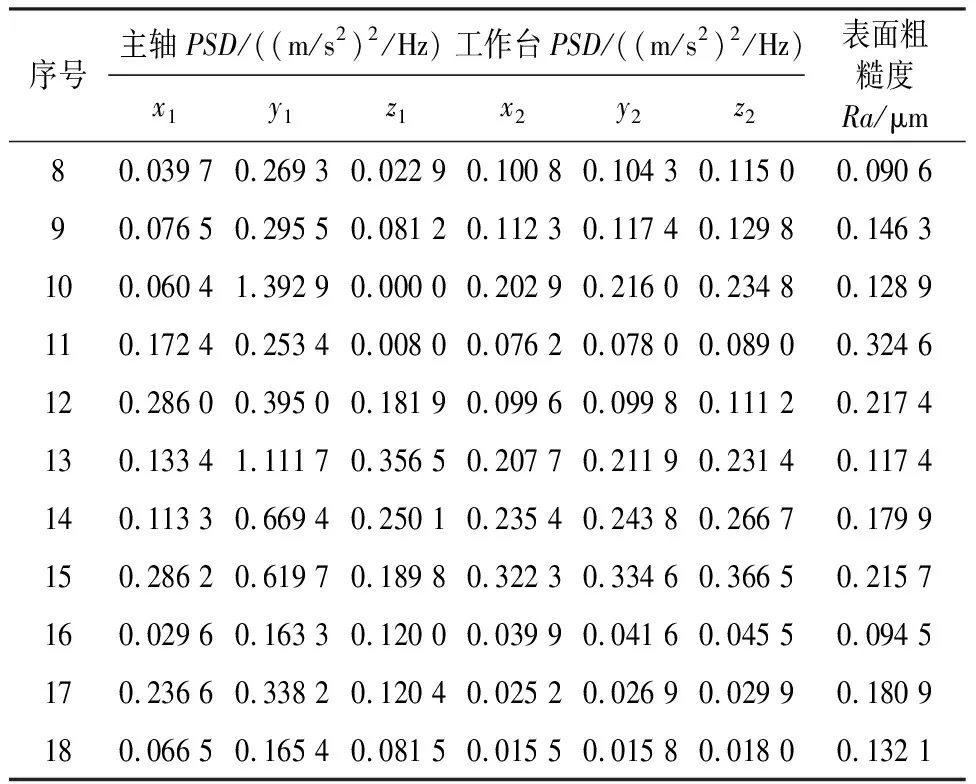
续表3

从表3不难看出，振动信号数据结构依然复杂，难以看出这些功率谱密度数据与表面粗糙度的关系。假设这些数据与表面粗糙度值存在线性关系，利用SPSS软件进行多元线性回归分析，对数据的自相关性和共线性进行诊断，分析结果如表4所示。

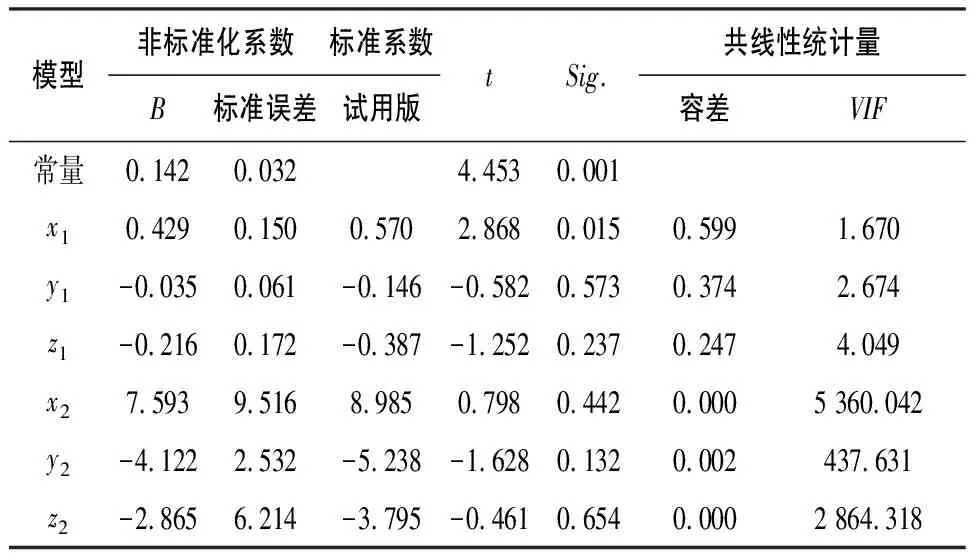
表4 系数及共线性诊断表

通过线性检验得到调整R2为0.598，说明该线性回归模型与原数据的拟合程度不高；6个变量经过t检验，只有x1的置信度<0.05，即说明主轴x方向上的振动信号功率谱幅值对表面粗糙度值的影响是显著的；共线性诊断统计量中，若VIF统计量>10，则说明数据之间的共线性层度小，可忽略不计，x2、y2、z2的VIF值远大于10，说明数据之间共线性层度较高，需对数据结构进行简化处理。

先对数据进行探索性研究，利用因子分析法中主成分分析法对数据进行降维处理(见表5)。

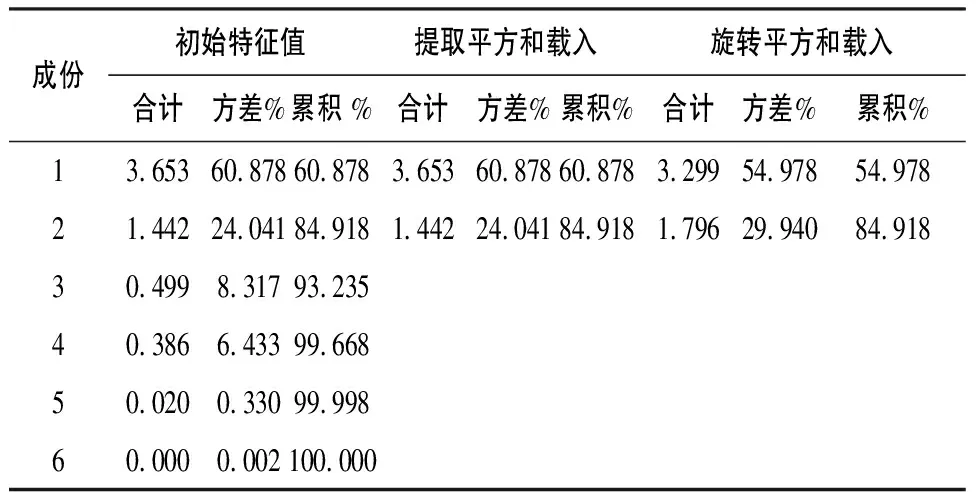
表5 成分信息含量

对数据进行主成分分析适度检验发现KMO值较低，表示数据量不够，但通过了Bartlett球形检验。从整体上看，虽然实验数据不足，但依然可以进行主成分分析。

从表5可以看出，主成分前2项就可以涵盖原始数据近85%的信息量，所以可以用这2项指标代表前面的6项指标。从后面的成分旋转矩阵可以看出成分1主要表示工作台3个方向的功率谱幅值，成分2主要表示主轴x和z方向上的功率谱幅值，而主轴y方向的功率谱幅值没有体现在表中，这可能是因为该数据成分比较均衡地分布在两个主成分中。

虽然存在误差，但不难看出主成分分析方法能够有效区分主轴和工作台的振动信号。可以合理猜测，随着数据量的提升，主成分分析法对数据的分类就越精确，这说明该方法有助于高速铣削振动信号的特征分类。

对9 000Hz处的功率谱幅值数据做相同处理。

先假定6个变量与表面粗糙度存在线性关系，进行自相关和共线性检测，经SPSS数据处理后发现，调整R2为0.41，说明该线性拟合模型仅能反映原始数据的41%；t检验的显著性水平只有x1低于0.05，说明主轴x方向上9 000Hz处的功率谱幅值对表面粗糙度的影响是显著的；通过共线性诊断发现，x2、y2、z2处的VIF值远大于10，故判断数据间存在多重共线性，需对数据简化处理。

通过SPSS软件对9 000Hz处的功率谱幅值数据做主成分分析，结果显示，前2项主成分反映原始数据的84.824%，将近85%，可以用2个主成分表示原始数据。第1个主成分主要反映工作台3个方向上的功率谱幅值，第2个主成分主要反映主轴3个方向上的功率谱幅值。

整体上看，主轴x方向上的振动信号对表面粗糙度的影响程度最大，同一部位不同方向上的功率谱幅值存在多重共线性，利用这一点可以大大简化数据结构，但这些数据特点还不能反映各部位两高阶频率的功率谱幅值对表面粗糙度的影响程度。从多元线性回归分析结果可以看出，这些变量与表面粗糙度的线性拟合程度很低，不适合直接做线性回归。根据一些专家学者的研究[8]，表面粗糙度与铣削参数之间的关系可用指数模型表示，所以假定表面粗糙度与振动特性参数的关系是指数关系，那么可以先求出数据的对数值，再利用SPSS软件进行多元线性回归分析，即可求出回归模型。

3 求解回归模型

3.1 振动信号的功率谱幅值的处理方案

通过之前的数据分析可以发现6 760Hz和9 000Hz的功率谱幅值都分别存在多重共线性，但并不能判断两组数据之间不存在线性关系，故综合所有振动信号数据进行主成分分析，结果如表6。

适度检验结果中KMO值为0.506，数据量略有不足，但通过了Bartlett球形检验，表明这些数据使用主成分分析是较为合理的。从表6可以看到前3项主成分能涵盖原始数据89.719%的信息，可将这些信息分为3类，每一类主成分中的变量之间存在线性关系。第1类主成分涵盖了工作台90%以上的振动信息，第2类主成分主要包括主轴y和z方向的振动信息，第3类主成分则包含了主轴x方向上的振动信息。

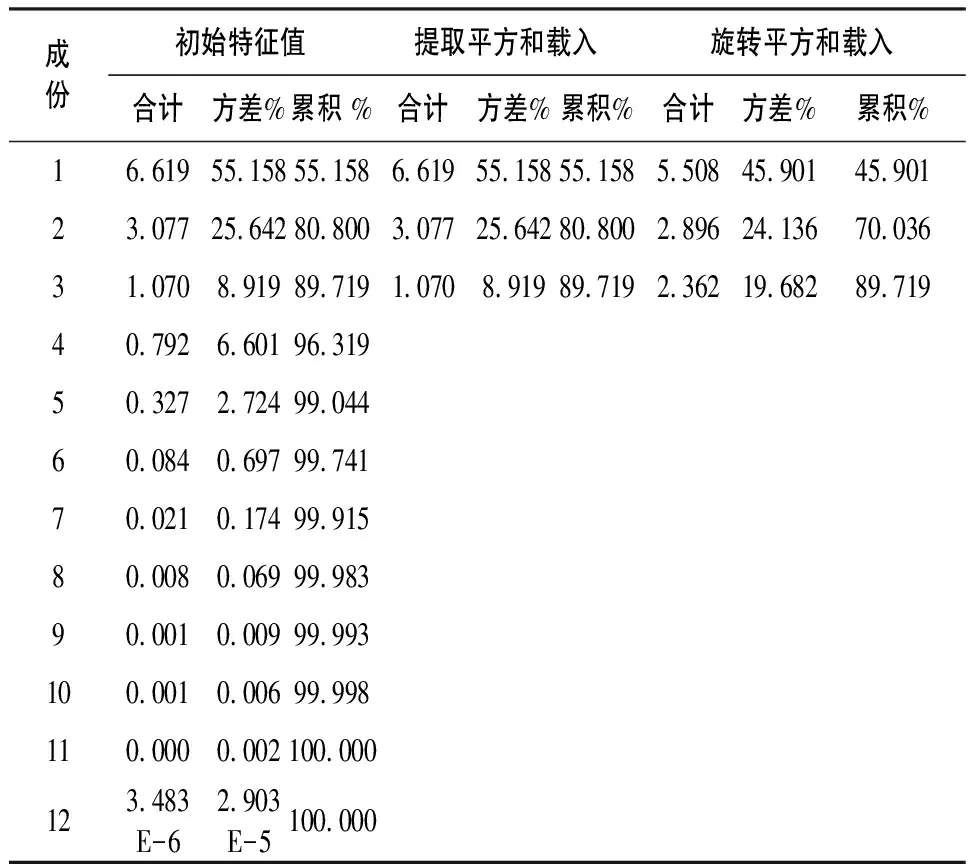
表6 成分信息含量

由于同一主成分内的变量间存在线性关系，故可用1个变量表示该成分的振动特性，选择主成分内原始信息含量最高的变量作为影响表面粗糙度的因素，因此选择工作台y方向9 000Hz处的功率谱幅值、主轴y方向9 000Hz功率谱幅值和主轴x方向6 760Hz处的功率谱幅值3个变量作为振动特征量。各个振动特征量与其组内其他变量的线性关系通过线性回归得到，结果如式(2)-式(4)所示。

第1主成分：

y高2=1.027x高2-0.067=

0.966z高2-0.095=

5.133x低2+0.512=

5.004y低2+0.524=

4.473z低2+0.513

(2)

第2主成分：

y高1=5.094y低1+0.894=

1.209z高1+2.894=

7.185z低1+2.860

(3)

第3主成分：

x低1=0.148x高1+0.017

(4)

式中，角标“低”指6 760Hz，角标“高”指9 000Hz，角标“1”表示主轴，角标“2”表示工作台。

综合前述分析和式(2)-式(4)可知，9 000Hz处的功率谱密度幅值对表面粗糙度的影响程度比6 760Hz处的大，即高频振动对表面粗糙度的影响较大；x方向上的功率谱密度幅值对表面粗糙度的影响程度比其它方向大，即刀具进给方向的振动特性对表面粗糙度的影响较大。

3.2 建立指数模型

由于试验中铣削宽度只选择了2个水平，且铣削宽度对表面粗糙度的影响并不显著，所以这里计算时忽略铣削宽度，这给数据分析带来一定的误差。

假定表面粗糙度与铣削工艺参数和振动特征量之间存在指数关系，先计算铣削工艺参数、振动特征量和表面粗糙度的对数值，再利用SPSS软件进行多元线性回归分析(表7)。

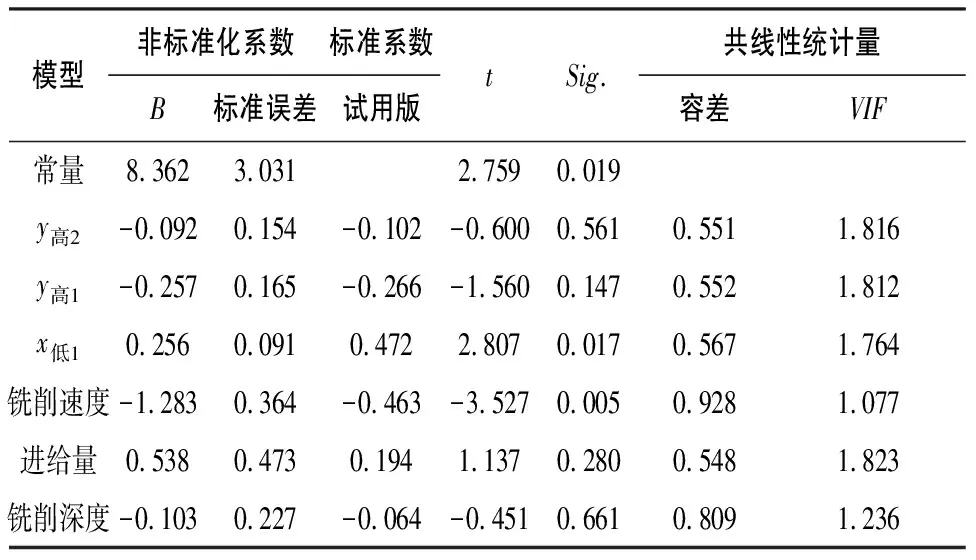
表7 系数检验表

该分析得到调整R2值为0.727，说明该回归模型能反映原始数据72.7%的信息量，DW统计量接近2，说明每组数据之间的自相关程度非常低，即每组实验数据之间相互独立。所以该模型能比较完善地反映表面粗糙度、铣削参数和振动特征量的关系。

从表7可以看出各因素对表面粗糙度的影响程度。通过t检验的结果可以知道，铣削速度对表面粗糙度的影响最为显著，其次影响程度从高到低是主轴x方向6 760Hz(主成分3)、主轴y方向9 000Hz(主成分2)、进给量、工作台y方向9 000Hz(主成分1)和铣削深度。进给量、铣削深度、主成分1对表面粗糙度的影响程度都非常低，分析原因有两点：从实验设计上看，设计的是三因素三水平的正交试验，进给量和铣削深度因为实验条件限制的原因设定范围非常小，因而对表面粗糙度的影响较小；从振动形式上看，工作台处于固定状态，主轴在加工时一直保持高速旋转，主轴的振动属于自激振动，工作台的振动属于强迫振动，高速铣削过程中自激振动往往强于强迫振动，自激振动在刀具和工件之间相对振动中起主导作用，所以工作台的振动特性对表面粗糙度的影响程度非常小。

综上所述，高速铣削钛合金表面粗糙度与铣削参数、各振动特征量之间的指数关系式为：

(5)

式中，z1表示第1个主成分中工作台y方向9 000Hz处的功率谱幅值，z2表示第2个主成分中主轴y方向9 000Hz功率谱幅值，z3表示第3个主成分中主轴x方向6760Hz处的功率谱幅值。

结合前面的分析和式(5)可以看出高频处功率谱幅值对表面粗糙度的影响是比较显著的，特别是x方向，即刀具进给运动方向的振动特性。这一点说明在高速铣削过程中主轴和工作台的高频振动特性对加工表面粗糙度的影响较大。由于主轴和工作台的高频动态特性不仅与自身固有属性有关，还与外界激励，如环境噪声、铣削用量等有关。因此，一方面可以通过提升主轴和工作台的强度和刚度来改善该部位的高频动态特性；另一方面可以通过合理设置铣削参数，使主轴和工作台的高频动态特性控制在适当的状态，进一步改善加工质量。具体的改善措施还有待深入研究。

4 结语

基于振动信号功率谱分析，研究了高速铣削钛合金振动特性对表面粗糙度的影响规律，通过主成分分析法简化了振动信号数据量，并用多元线性回归分析得到表面粗糙度关于振动特征量和铣削参数的指数回归模型。具体得到以下结论：

通过共线性检测发现振动信号功率谱幅值之间存在多重共线性，将振动信号数据进行主成分分析，发现这些数据可分为3类，第1类为工作台的振动信号，第2类为主轴y、z方向的振动信号，第3类为主轴x方向的振动信号。

结合主成分分析和线性回归分析可知，9 000Hz处的功率谱密度幅值对表面粗糙度的影响程度比6 760Hz处的高，即高频振动对表面粗糙度的影响较大；x方向上的功率谱密度幅值对表面粗糙度的影响程度比其他方向高，即刀具进给方向的振动特性对表面粗糙度的影响较大。

通过多元线性回归得到表面粗糙度关于振动特征量和铣削参数的指数回归模型，并指出可以通过改善主轴和工作台的强度、刚度和设置合理的铣削参数来提升加工表面质量。