考虑安装误差的圆柱摩擦轮接触分析

周磊， 陆天炜 ，李永健， 邬霞

(西南交通大学 a. 机械工程学院; b. 牵引动力国家重点实验室,四川 成都 610031)

0 引言

圆柱摩擦轮传动是利用两个相互压紧的摩擦轮之间的摩擦力传递动力。圆柱摩擦轮传动因具有结构简单、制造方便、传动精度高、使用维修方便等优点而广泛运用于矿山机械、精密测量仪器等领域中，如水泥回转窑、三坐标划线机、大型天文望远镜等。在圆柱摩擦轮传动的实际安装中，不可避免地存在安装误差，这些安装误差对圆柱摩擦轮的接触受力产生了影响。

刘波等[1]考虑了安装偏心对摩擦轮传动精度的影响进行了分析。肖友刚等[2]对回转窑托轮和滚圈在斜压接触的情况下进行了有限元分析。李学军等[3]运用有限元方法对回转窑支承结构托轮平行与呈最大偏斜角时的接触问题进行了研究。黄传清等[4] 27-29对轴线交叉时两圆柱体的接触问题进行了研究。

圆柱摩擦轮传动时，受较大的压紧力作用，在不考虑制造误差和轮轴的弹性变形时，由于安装误差的存在，导致摩擦轮的表面接触区受力情况的改变，可能会使摩擦轮表面因应力集中而产生接触疲劳破坏。本文利用ANSYSWorkbench对3种安装误差情况进行摩擦轮有限元接触分析。分析结果对圆柱摩擦轮传动的设计及安装有一定的指导意义。

1 正确安装圆柱摩擦轮的接触分析

在不考虑制造误差等其他因素时圆柱摩擦轮传动正确安装状态如图1(a)所示。圆柱摩擦轮的主动轮和从动轮在压紧力Q的作用下产生接触，可利用赫兹理论进行静态接触分析。主动轮和从动轮的接触情况如图1(b)所示，接触区宽度为2a，长度为B的矩形，压力分布为p(x)[5]:

(1)

其中，P=Q/B，a为半接触宽度，由式(2)得到:

(2)

接触区的最大接触应力在接触区中间并由式(3)得到：

(3)

图1 圆柱摩擦轮安装

2 安装误差对圆柱摩擦轮接触的影响

2.1 安装偏心

安装偏心指圆柱摩擦轮的回转中心和几何中心不重合，会导致圆柱摩擦轮在转动的过程中心距不断变化，当加压装置为恒压加压时，圆柱摩擦轮的压紧力也不断变化。如图2所示，主动轮和从动轮的几何中心和回转中心分别为o1、o2和o3、o4；e1、e2分别为主动轮和从动的偏心距；r1、r2分别为主动轮和从动轮的半径。现只考虑安装偏心对圆柱摩擦轮接触应力增加最严重的情况，为便于分析作如下假设：

1) 圆柱摩擦轮的压紧力由弹簧产生，弹簧刚度为k；

2) 两轮初始回转中心距为l0=r1+r2-(e1+e2)，初始压紧力为Q0；

3) 仅考虑压紧力对两轮静态接触的影响。

基于上面的假设，当主动轮与从动轮的回转中心距达到最大值时，即lh=r1+r2+(e1+e2)，压紧力也达到最大值Qm=Q0+2k(e1+e2)，将Qm带入式(3)即可求得接触区的最大接触应力。

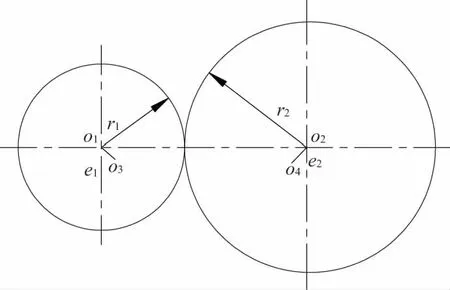
图2 安装偏心示意图

2.2 扭转角和偏转角

由于安装误差，主动轮和从动轮的轴线在空间位置的角度可分解到两个方向的夹角[6]，图3中，α为偏转角，β为扭转角。

如图3(a)所示，当主动轮和从动轮的轴线存在偏转角时，主动轮和从动轮的接触从线接触变为点接触，从而使初始接触点处的接触应力变大。

如图3(b)所示，当主动轮和从动轮的轴线存在扭转角时，初始接触由线接触变成点接触，且该点位于线接触时初始接触线的中点。当扭转角较小时，接触区为不完全椭圆[4]27。

图3 夹角示意图

3 ANSYSWorkbench圆柱摩擦轮接触分析

如图4所示，为某实验台的圆柱摩擦轮传动。现以该传动为例，分别考虑正常安装和存在安装误差的情况下，利用Workbench进行接触分析，得到不同安装条件下摩擦轮的接触应力情况。此圆柱摩擦轮传动采用恒压压紧装置，压紧力由普通圆柱螺旋弹簧产生；从动轮的滚动轴承座固定在直线导轨上，主动轮的轴承座固定在机架上；摩擦轮材料为钢对钢，无润滑，摩擦系数取0.15[7]，详细参数见表1。

图4 圆柱摩擦轮传动示意图

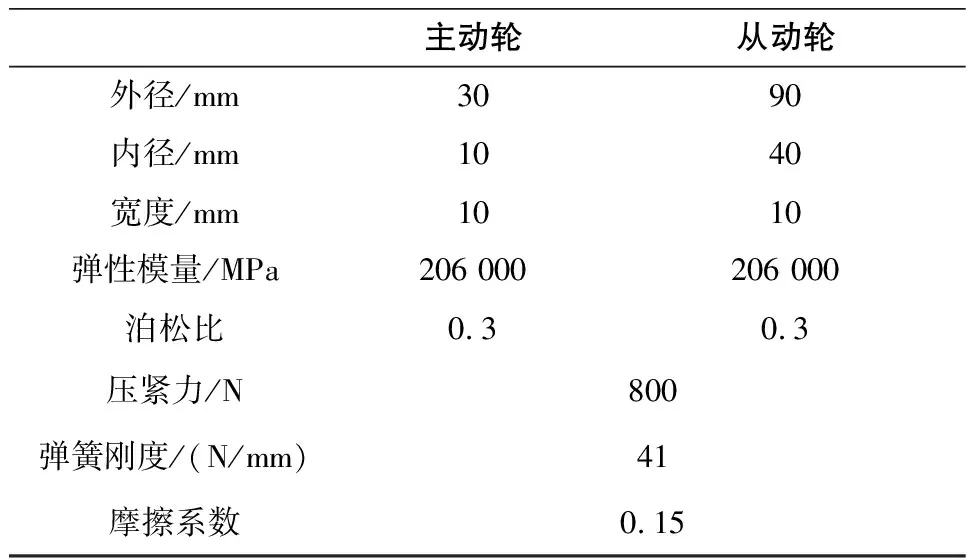
表1 圆柱摩擦轮的基本参数

3.1 有限元模型

忽略键槽倒角等细节部分，将两轮简化为两个空心圆柱，按照表1中的参数建立圆柱摩擦轮的三维模型。为方便对摩擦轮进行网格划分，将主动轮和从动轮分别分割成3个区域如图5所示。对圆柱摩擦轮三维模型进行网格划分，并对接触区进行局部网格细化，细化单元大小为0.05 mm，如图6所示，模型网格划分后共48 613个单元，节点为170 606个。

网格划分完后，定义接触对：将主动轮接触区表面定义为接触面，从动轮接触区表面定义为目标面；接触类型设置为frictional，摩擦系数取0.15；接触算法采用增强拉格朗日法。

根据圆柱摩擦轮的受力情况，主、从动轮施加载荷边界条件如图7所示，在主动轮的内孔面施加固定约束；在从动轮的内孔面施加给定位移约束，并设定两轮接触面的公法线方向自由度为无约束，其他两个方向为0；在从动轮内孔面施加轴承载荷，模拟主、从动轮之间的压紧力,并设置载荷步数为2。

图5 分割模型

图6 网格划分

图7 边界条件和载荷

3.2 仿真结果及分析

经过仿真计算得到各安装状况下的圆柱摩擦轮的接触应力。如图8(a)所示，正确安装时圆柱摩擦轮接触区为狭长矩形，最大接触应力为506.45 MPa和式(3)得到的理论值506.16 MPa基本一致；如图8(b)所示，在摩擦轮的端面接触区的最大接触应力有所减小，这是由于端部材料受接触压力的作用时能够在轴线方向变形所导致的，表明与赫兹理论相比有限元仿真更符合实际。

图9(a)和图9(b)分别为偏心距e1+e2=0.3mm和e1+e2=0.6mm时圆柱摩擦轮的接触应力图。由图可知，当圆柱摩擦轮存在安装偏心时，其接触应力分布情况与正确安装时基本一致，最大接触应力有所增加,图9(a)和图9(b)中最大接触应力比正常安装时的最大接触应力分别增加了1.53%、2.99%。

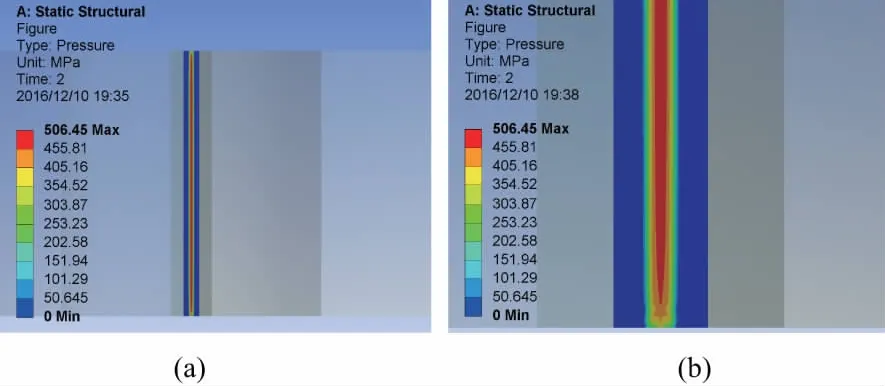
图8 正确安装时圆柱摩擦轮接触应力图

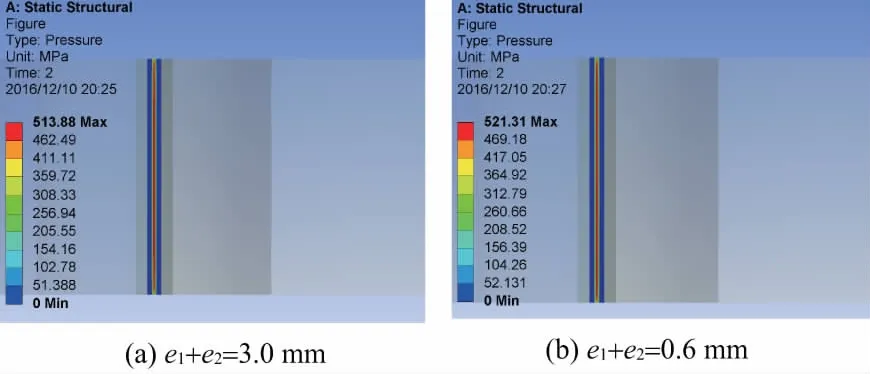
图9 安装偏心时圆柱摩擦轮接触应力图

图10(a)和图10(b)分别为偏转角α=0.1°和α=0.4°时圆柱摩擦轮的接触应力情况。可以看出，由于主动轮和从动轮的轴线存在偏转角，接触区由正常安装时的狭长矩形变成近似半椭圆形状，接触压力最大值靠近端部，且由最大值处沿半椭圆的长轴方向急剧减小。当偏转角α=0.1°时，最大接触应力为1 009.9 MPa，比正常安装时增加了99.41%；当偏转角α=0.4°时，最大接触应力为1 581.7 MPa，比正常安装时增加了212.32%。由图10(a)和图10(b)可以发现，随着偏转角增大，接触区的大小也随之变小。

图10 安装存在偏转角时圆柱摩擦轮接触应力图

当圆柱摩擦轮安装存在扭转角时的接触应力情况如图11所示。由图11可知，接触应力分布与正确安装时差别不大，但最大接触应力增加。当扭转角β=0.1°时，最大接触应力为509.85MPa，当扭转角β=0.4°时，最大接触应力522.19MPa，与正常安装时分别增加了0.73%与2.62%。

仿真还得到了在各类安装误差情况下摩擦轮最大接触应力随安装误差的大小的变化情况。如图12(a)、图12(b)和图12(c)所示，最大接触应力随安装误差增大而增大。图12(a)为弹簧刚度分别为31 N/mm、41 N/mm、51 N/mm时，摩擦轮的最大接触应力与偏心距的关系。由图12(a)可知，摩擦轮的最大接触应力随偏心距的增大而增大，同时偏心距对最大接触应力的影响程度还随弹簧刚度的增加而增加。比较图12(b)和图12(c)，偏转角比扭转角更容易造成摩擦轮的偏载和应力集中，导致最大接触应力急剧变大。

图11 安装存在扭转角时圆柱摩擦轮接触应力图

图12 圆柱摩擦轮最大接触应力图

4 结语

通过对圆柱摩擦轮传动在正确安装和存在安装误差时摩擦轮接触情况的分析，并利用ANSYSWorkbench对一对圆柱摩擦轮传动在不同安装条件下进行了接触仿真分析，可得到如下结论：

1) 赫兹理论对圆柱摩擦轮的接触分析在接触区的大部分区域适用，但在圆柱摩擦轮的端部有所偏差，有限元分析更符合实际。

2) 安装时存在偏转角会导致摩擦轮接触产生严重的偏载和应力集中，最大接触应力也随之增大而急剧增加，其对圆柱摩擦轮接触的影响比存在扭转角时更大。

3) 安装偏心对圆柱摩擦轮接触的影响还与弹簧刚度有关；存在相同的安装偏心时，所用弹簧刚度越大，摩擦轮的最大接触应力也增加得越多。

4) 在实际圆柱摩擦轮的设计和安装中，应该合理设计弹簧的刚度以减小安装偏心对摩擦轮最大接触应力的影响；安装时应尽量避免存在偏转角和扭转角以防止应力集中和偏载。