运用变式教学,提高教学效率
江苏省扬州市江都区实验初中 张 静
一、变式教学在概念教学中的运用
数学概念通常比较抽象,学生会觉得比较枯燥,短短的一句话并不能让他们理解概念的内涵与外延,会造成相关知识学习上的困难。而运用变式教学,能从知识的内在联系及变化上对概念进行剖析,学生就不会觉得枯燥,对知识也会印象更深刻。
【教学案例1】一元一次方程概念的理解
例题:下列哪些是一元一次方程?
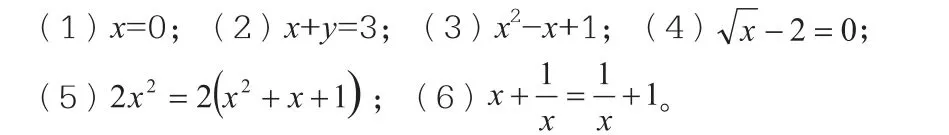
【设计意图】以往学生对一元一次方程的概念一知半解的原因就是对其本质特征“一元”“一次”“整式”的理解不深刻,所以在教学中,我采用“一元一次方程如何判断”到“满足什么条件成为一元一次方程”进行变式教学,使学生很好地掌握知识点。
二、变式教学在例题教学中的运用
在变式教学的实施过程中,以例题的变式教学最为普遍。例题的变式可以变换题目的条件、结论或表现形式,而题目本身的实质不变,使之成为一道新题。
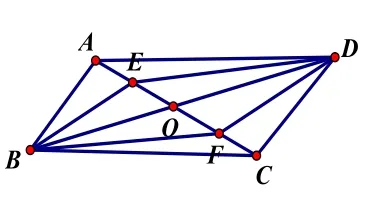
【设计意图】变式1让学生通过已有的解题经验和数学知识,把知识形成过程变为知识发生、发展的创造过程,由特殊推广到一般,培养学生的创新意识和归纳能力。变式2考查学生对敏感词“直线”是否熟悉,图形的变化对画图能力较弱的学生具有一定的挑战性。变式3的图形建立在原图的基础上,由于上面问题的解决,此时解决这个问题顺理成章,让学生体会到成功的快乐。这三个变式都是对问题的条件进行变化,由简到难,增加题目挖掘的深度和广度。
三、变式教学在习题教学中的运用
习题的多层次变化能激发学生学习数学的热情和积极性,提高学生参与创新与探究的意识,开拓学生的思维,使学生真正得到学习能力的提升。
【教学案例3】二次函数的应用(面积最大问题)
例题:某农场要用60米长的篱笆建一个矩形的养鸡场,鸡场的一面靠墙(墙足够长)。
1.生产流通环节的财税优惠政策。针对长期以来对化肥生产企业实行的减免税政策,开始恢复到正常状态,即从减免税恢复到征收13%的低税率。从2017年7月1日起,化肥生产企业的增值税一般税率从13%进一步下调至11%;2018年3月,我国规定对销售或进口化肥适用的税率进一步降低为10%。
(1)如果要围成面积是400平方米的矩形,则矩形的长和宽分别是多少?
(2)能围成面积比400平方米更大的矩形吗?
变式1:(1)若墙长为28米,还能围出面积为450平方米的矩形吗?这时矩形的最大面积是多少?
(2)若墙长为a米,a的取值对矩形的最大面积有影响吗?有怎样的影响?
变式2:(1)养鸡场建这么大,不容易管理,也不卫生,如果仍然一边靠墙(墙足够长),再在中间用篱笆建一道隔栏,使原来的矩形分成两个全等的矩形,这时如果要使养鸡场的面积最大,应如何建?最大面积是多少?
(2)如果建两道隔栏,三道隔栏,……,n道隔栏呢?你有什么发现?
【设计意图】首先建立函数模型,寻找变量之间的关系,再探讨中间隔栏由1变化到n的过程中,再一次经历由特殊到一般的过程,强化归纳能力。
【教学案例4】圆中线段和差关系
例题:如图,△ABC是⊙O的内接三角形,点D是劣弧BC上一点,连接AD、BD、CD,若△ABC为等边三角形,则AD、BD、CD有什么关系?
变式1:若△ABC为等腰直角三角形呢?若△ABC是顶角∠BAC为120°的等腰三角形呢?若△ABC是顶角∠BAC为36°的等腰三角形呢?

变式2:△ABC是⊙O的内接三角形,点D是圆上任意一点,连接AD、BD、CD,若△ABC为等边三角形,则AD、BD、CD有什么关系?
【设计意图】在变式1这类习题的解答中,学生容易出现就题解题的情况,思维无法得到连续性的发展,首先利用特殊点猜测三条线段之间的关系,然后可以有多种方法解决例题,在方法不变的情况下,将三角形进行变化,从而根据不同的特殊三角形得到规律的结论,形成一个解题模型。在变式2中,点D的位置不确定,由特殊到一般,分类讨论,学生思维的严谨性也逐渐被培养出来了。
学生在独立解决问题时表达出来的思路狭窄、应变能力差,往往与教师讲解习题时习惯就题论题、缺少变式、缺少拓展有关,在学生认知能力可及的情况下,教师要有目的、有计划地对概念、例题或习题进行变式,使学生从不同角度、不同层次、不同背景下重新认识数学问题,引导学生从变中发现不变的规律,帮助学生融会贯通所学的知识,促进学生思维的发展,提高学生解决问题的能力,从而让学生能够在学习中“以不变应万变”。
四、运用变式教学应注意的几个问题
在具体的教学实践中,一定要注意变式要有代表性、层次性、灵活性和开阔性。数学教学不仅是向学生传授知识,更重要的是培养学生的思维能力。变式教学是启迪、拓展学生思维的重要方法,更是立足教材、摆脱题海、减轻学生负担、提高教师业务素质的有效途径,因此,加强变式教学对提高课堂效率必定大有裨益。

