SiC纤维增强Ti17合金复合材料轴向残余应力的拉曼光谱和X射线衍射法对比研究∗

黄浩 张侃 吴明† 李虎 王敏涓 张书铭陈建宏 文懋‡

1)(中国航发北京航空材料研究院钛合金研究所,北京 100095)

2)(吉林大学,材料科学与工程学院,超硬材料国家重点实验室,吉林大学汽车材料重点实验室,长春 130012)

(2018年6月12日收到；2018年7月24日收到修改稿)

1 引 言

SiC连续纤维增强钛基复合材料(SiCf/Ti)由于具有高比强度、高比刚度、优良的耐高温及抗蠕变和抗疲劳等性能,被认为是理想的轻质耐高温结构材料,在提高强度和刚度的同时,实现了大幅减重[1−3].由于SiCf/Ti复合材料具有这些优良的性能,在高推重比发动机和超音速空天飞行器中展现了良好的应用前景,已成为高推重比发动机所必须的关键新材料[4,5].SiCf/Ti复合材料制备过程中要经过高温热压或热等静压成型,该成型温度范围一般在920—980◦C,由于SiC纤维和钛合金基体的热膨胀系数存在较大差异,冷却过程中复合材料的界面处产生热残余应力是不可避免的,致使钛合金基体和SiC纤维在沿着纤维轴向方向分别处于拉伸和压缩状态.在不同的钛合金体系、纤维体积分数和制备工艺下,已报道的SiCf/Ti复合材料的热残余应力能达到基体材料拉伸强度的30%—80%[6].高的热残余应力加上外加的拉伸应力,会使钛合金基体过载(超过其屈服强度),在SiCf/Ti复合材料界面附近产生裂纹,影响其纵向强度和高周疲劳性能[7].此外,热残余应变和应力在服役过程中因热循环而产生反复也会导致热疲劳.在横向载荷作用下,界面处的应力突变点将会导致裂纹萌生和界面脱黏,影响SiCf/Ti复合材料的横向强度[8].热残余应力对SiCf/Ti复合材料的寿命预测也起到重要影响.为了让SiCf/Ti复合材料在各种服役环境下能获得高性能和保证可靠性,详细分析复合材料中的热残余应变和应力状态显得尤为重要.

虽然目前大量的理论计算用来预测热残余应力的大小及其在复合材料中的分布[9,10],但是由于不同的热成型工艺和基体材料的热处理工艺会产生复杂的界面微观组织结构,需要采用实验方法测量其应变和应力状态验证理论预测结果.常用的实验方法包括选择基体腐蚀法、X射线衍射法、中子衍射法和拉曼光谱法等[11−14].选择基体腐蚀法通过腐蚀基体材料后测量SiC纤维的伸长量获得纤维的轴向应变力,但由于该方法很难准确确定腐蚀深度和测量腐蚀前后的纤维伸长量,导致误差较大.X射线衍射法或中子衍射法主要通过测量基体合金衍射峰的峰位移动获得基体材料的平均应变,进而计算出应力状态.目前X射线衍射法测量SiCf/Ti复合材料应力时,主要集中在箔压法制备的纤维横向排布的复合材料中,通过双轴应力模型获得σ11作为轴向应力状态.但复合材料中由于纤维的束缚,将Z轴方向的应力近似为零(双轴模型),与真实情况差距较大,亟待开展三轴应力模型对复合材料应力的分析与表征.拉曼光谱法是利用石墨C涂层在无应力和有应力状态下振动峰位的变化来计算纤维表面的残余应力值.由于拉曼测试中激光点的直径通常小于1µm,对比前面三种方法,拉曼光谱法的分辨率更高,能够测量纤维表面C涂层微米区域的受力状态.拉曼法被广泛用于C纤维增强树脂基复合材料的残余应力测试[15],但在SiCf/Ti复合材料中仍然关注较少.

本文采用化学气相沉积(chemical vapor deposition,CVD)的方法在单丝SiC纤维表面沉积厚度约为2.5µm的热解碳涂层,随后采用基体涂层法利用DPS-III型高真空对靶磁控溅射设备在SiC纤维表面沉积近β合金Ti17(名义成分wt%:Ti-5 Al-2Sn-2Zr-4 Mo-4Cr)制备先驱丝,然后将先驱丝切成一定的长度,并规则排布放入Ti17合金的中空圆柱筒内进行电子束封装,最后在920◦C/120 MPa/2 h下热等静压成型,制备成纤维体积含量Vf∼48% 的SiCf/C/Ti17复合材料.为了研究复合材料界面的应力情况,首先采用拉曼光谱法测试了SiCf/C/Ti17复合材料的残余应力,再结合X射线衍射的结果共同判断该复合材料内SiC纤维的残余应力.

2 拉曼光谱法应力测量

2.1 测试样品

如图1(a)所示,将Ti17合金基体从SiCf/C/Ti17复合材料的末端去除露出SiC纤维,该部分纤维用于无应力状态下的拉曼光谱测试.而未腐蚀的完整复合材料截面用于有应力状态下的拉曼光谱测试,如图1(b)所示.通过对比以上两种情况下的SiC纤维表面C涂层的拉曼光谱峰位的移动用于计算复合材料中SiC纤维表面C涂层的残余应力,并将此值作为SiC纤维的应力.

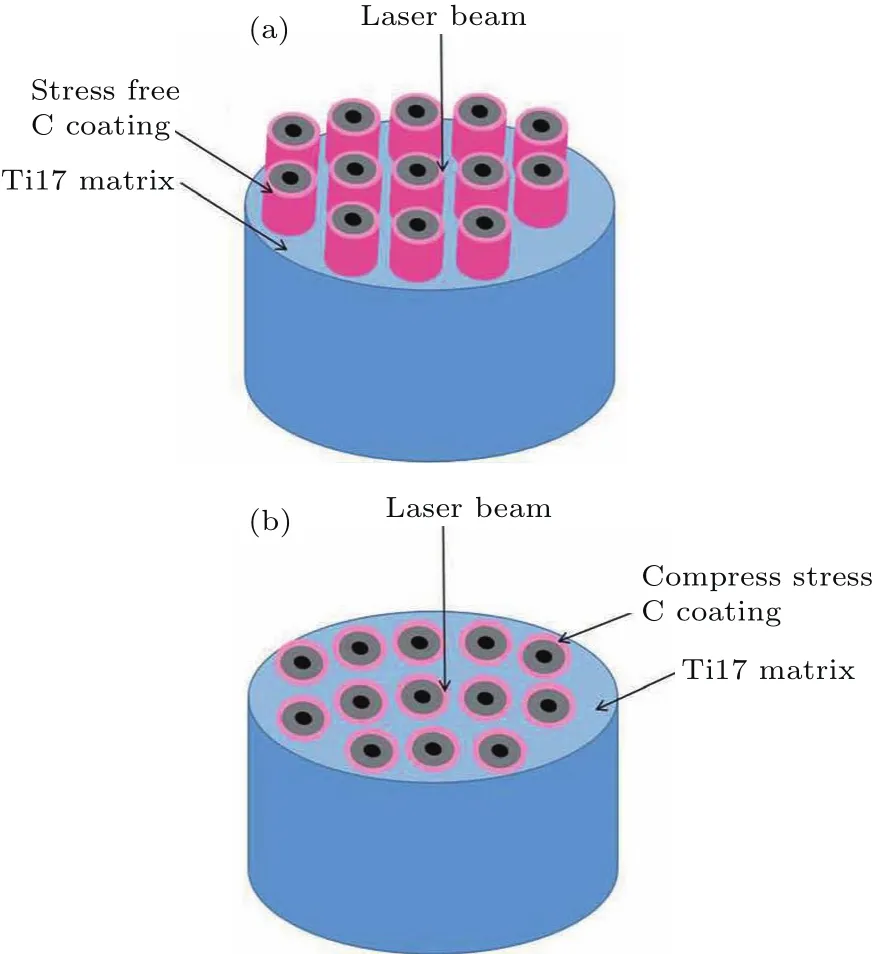
图1 涂覆C涂层的SiC纤维拉曼光谱法残余应力测试的样品示意图Fig.1.Schematic image of sample preparation for characterizing the residual stress of a carbon coated fiber by Raman spectra.

2.2 测试原理

在出现应变时固体中声子模的动力学方程为[16]

式中ui为晶胞内两个原子相对位移的i分量,m为两个原子的约化质量,=为无应变时声子模的有效弹簧常数.

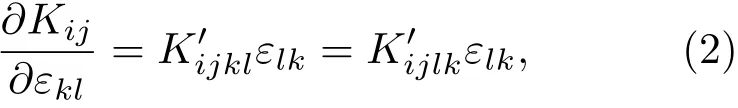
方程(2)表示在应力εkl作用下弹性常数的变化,其中i,j,k和l代表晶轴.

根据方程(1)可以推导出应变晶格的声子频率.对于每个晶胞中有4个原子的石墨而言,3个声学模和9个光学模得到了一个12×12的久期行列式.晶格的六角对称导致了久期行列式在k=0时的因式分解,此时拉曼活性E2g2模可表示为

其中ωσ为应变相关的拉曼频率,ω0为无应变时的拉曼频率.方程(4)可以近似为

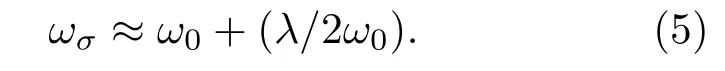
由于应变的剪切分量消失,久期方程(3)简化为

根据方程(6)得到

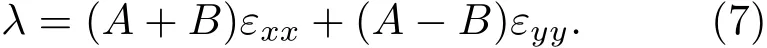
将石墨的应力-应变关系εxx=S11σ和εyy=S12σ代入到方程(7)和(5),得到应力相关的拉曼频率为

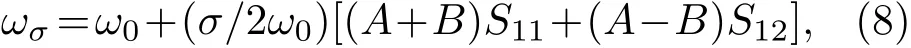
应变导致的拉曼频移∆ω为

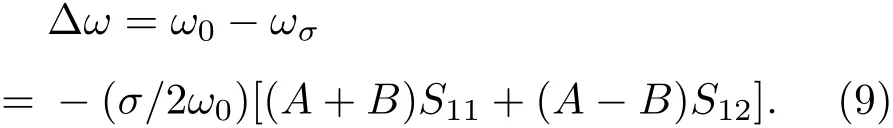
将石墨的弹性顺度常数值S11=0.98×10−3GPa,S12=0.16×10−3GPa[17]及描述应变作用下k=0时石墨光学支模弹性常数变化的唯象系数A=−1.44×107cm−2,B=±5.80×106cm−2[18]代入(9)式,得到C涂层所受应力σ与拉曼频移∆ω的关系.采用等应力传递近似,则SiCf/C/Ti17复合材料内SiC纤维的残余应力与拉曼光谱G峰频移的关系可以表示为

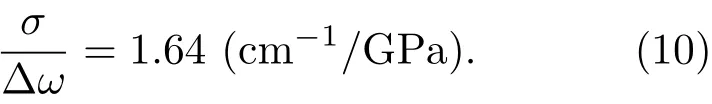
综上所述,采用拉曼光谱法测量SiC纤维表面C涂层在无应力和有应力状态下G峰的峰位变化,并通过方程(10)能够计算出SiCf/C/Ti17复合材料内SiC纤维所受残余应力的大小.

2.3 实验结果

图2(a)是制备态SiCf/C/Ti17复合材料的横截面扫描电子显微镜(SEM)图及能谱分析结果.由于在920◦C热等静压过程中Ti17合金基体与C涂层发生了界面化学反应,导致部分C涂层被消耗,SiC纤维被剩余C涂层和生成的致密的反应产物包围,复合材料内没有出现微裂纹.在复合材料的20个不同的界面位置测得剩余C涂层和反应层的厚度分别为∼1.4µm和∼1.3µm.根据图2(b)的界面区域透射电子显微镜(TEM)图及相应的选区电子衍射标定的结果可知,生成的界面反应产物为TiC.选区电子衍射是表征热解碳取向和织构的有力方法,Reznik和Hüttinger[19]根据热解碳方位角(orientation angle,OA)的大小将其分为以下四种结构:各向同性(isotropic OA=180◦)、低织构(low textured 80◦6OA6 180◦)、中织构(medium textured 50◦6OA 6 80◦)高织构(high textured OA6 50◦).因此本文利用高分辨透射电子显微镜(HRTEM)和选区电子衍射(SAED)观察了C涂层的微观结构,结果分别如图2(c)和图2(d)所示,该C涂层的(002)晶面大体上是平行于SiC纤维的轴向方向且垂直于纤维的径向方向排布,方位角∼42◦,表明其具有典型的高织构乱层石墨结构,可以近似为石墨结构来处理.乱层石墨的拉曼光谱通常会出现两个主要的特征峰,分别是源于布里渊区边界K点震动的具有A1g对称震动模式的D峰和对应于石墨布里渊区中心τ点拉曼活性震动的具有E2g对称性的G峰[20].其中,由于纤维表面高取向的C层中石墨平面平行于SiC纤维的轴向方向,所以代表石墨结构振动模式的G峰的波数更能反映出纤维轴向应力.在C纤维增强树脂基复合材料中,也选用G峰为目标峰,以其在承受应力前后峰位的变化用于测试C纤维的残余应力.因此,本文可以利用SiC纤维表面C涂层的G峰峰位的变化来测量SiCf/C/Ti17复合材料中纤维的残余应力.

图2 (a)SiCf/C/Ti17复合材料的横截面扫描电子显微镜图及能谱分析结果；(b)界面反应区的TEM图像以及界面反应产物SAED花样；(c)C涂层的HRTEM图像；(d)C涂层的SAED花样Fig.2.(a)The cross-sectional SEM image and corresponding EDS analysis of SiCf/C/Ti17 composite；(b)TEM image of interfacial zone and SAED patterns of interfacial reaction products；(c)HRTEM image and(d)corresponding SAED patterns turbostratic C coating.

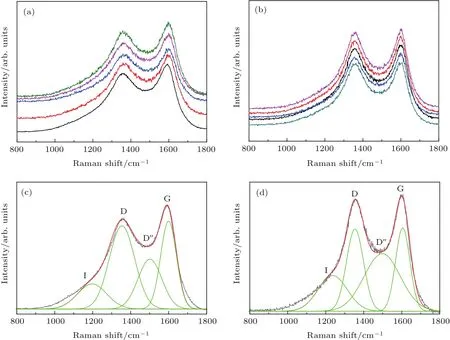
图3 SiC纤维表面C涂层的Raman光谱图 (a)无应力状态和(b)应力状态；拟合后的Raman光谱图,(c)无应力状态和(d)应力状态Fig.3.Raman spectra for C coatings coated on SiC fibers:(a)Stress free and(b)under stress；the fitting Raman spectra(c)stress free and(d)under stress.

分别在去除基体后的SiC纤维表面C涂层(无应力态)和复合材料内C涂层(应力态)处随机选取5个位置进行拉曼光谱测试,结果分别如图3(a)和图3(b)所示.由于仅采用D峰和G峰两个振动峰不能够完美地拟合拉曼光谱图,基于文献[21,22]报道,C的拉曼振动峰包含四个子峰,依次是:C涂层中存在芳香环、石墨晶格的乱序或sp2-sp3键合导致的I峰；对结构缺陷很敏感的D峰；间隙缺陷引起的D′′峰以及表明了石墨片层内存在有序结构的G峰.分别选取无应力状态和应力状态中其中的一条谱线,采用专业分析软件peakfit,对四个子峰均采用高斯型曲线进行拟合,拟合结果如图3(c)和图3(d)所示.无应力态SiC纤维表面C涂层的拉曼光谱中G峰的峰位为1599.3 cm−1,在应力的作用下G峰的峰位向高波数偏移,变为1603.4 cm−1,根据方程(10)计算得到C涂层的残余应力为−705.0 MPa,由于C涂层厚度较小,界面通过等应力传递,近似认为SiC纤维与C涂层具有相同的应力状态,残余应力为−705.0 MPa,呈现为压应力.Wang等[14]采用拉曼光谱法测量了纤维横向排布的SiCf/Ti-22 Al-26Nb复合材料内的残余应力,通过点腐蚀获得无应力状态C的拉曼光谱,得到表面涂覆了C涂层的SiC纤维的残余应力为−573 MPa.而刘斌等[23]用拉曼光谱研究了表面无C涂层的SiC纤维单丝的结构,直接测量SiC的振动峰,并与SiCf/Ti-6Al-4V复合材料内的SiC纤维拉曼光谱进行对比,在残余压应力的作用下复合材料内的SiC纤维的横向光学声子模向高波数移动,得到复合材料内纤维的残余应力为−381 MPa.

3 X射线衍射法应力测量

3.1 无应力样品制备

通过与制备复合材料同样的物理气相沉积(physical vapor deposition,PVD)工艺在Ti17合金基体上制备厚的Ti17合金涂层,然后把PVD Ti17合金进行封装和热等静压,并在550◦C下进行3 h去应力退火,获得PVD Ti17合金的无应力态d0.为了避免SiC纤维峰的干扰及减小测试过程中系统误差,我们选择测试基体钛合金的α-Ti(213)高角衍射峰,获得无应力态的d0=0.82 Å.

3.2 测试原理

X射线衍射可以通过测量不同方向上晶体材料中晶面间距来获得空间应变[24],通过sin2ψ法计算出应力值(d与sin2ψ的斜率).X射线衍射法测试靠改变ϕ与ψ来获得空间应变状态,靠衍射确定的应变态的基本关系如下[12,25]

εϕψ为实验室坐标下测量的应变,εij为样品坐标下的应变.

根据各向同性的弹性理论,应变εϕψ也可表达为如下方程:

σ11,σ22和σ33为样品坐标下的主应力；σ12,σ13和σ23为样品坐标下的剪切应力.通常σ13和σ23存在的情况下,d与sin2ψ的斜率不再是直线而发生劈裂,不存在的情况下,d与sin2ψ的斜率保持线性关系.

图4 SiCf/C/Ti17复合材料内纤维纵向排布的坐标示意图Fig.4.Schematic image of the coordinate system for crosssections perpendicular to the fibers directions.

对纤维涂层法制备的样品,纤维多为纵向排布,如图4所示.但在该排布下σ33为沿着纤维轴向方向的应力,由于纤维的束缚,该应力不可能释放为零.为了获得纤维纵向排布复合材料中沿轴向方向的应力σ33,采用三轴应力态来处理,为了计算出各应力张量的值,选取ϕ=0◦,45◦,90◦三个角度下分别进行不同ψ角度的测量.将ϕ=0◦,45◦,90◦和三轴应力张量代入方程(12)可获得:

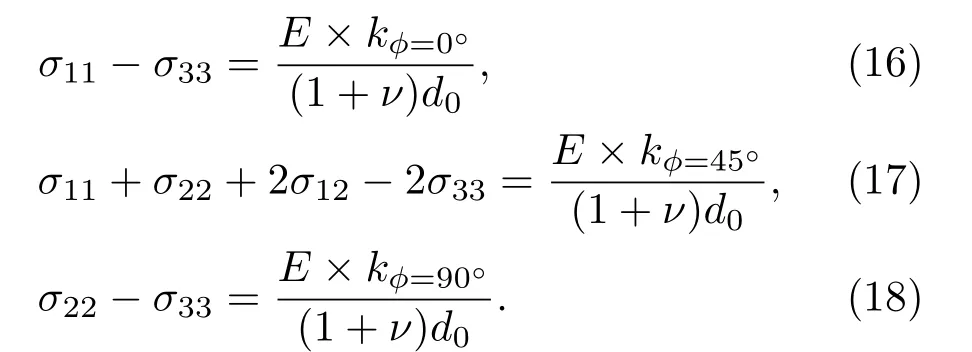
此外当ψ=0◦时,从方程(13)—方程(15)还可以获得三个截距,将三个截距取平均值=0◦,得到方程

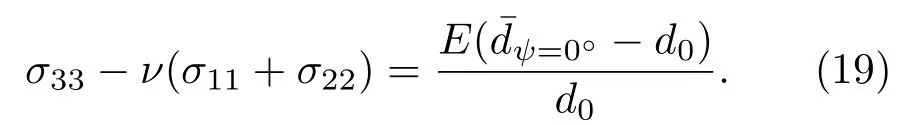
将无应力态的d0=0.8206 Å 代入, 再联立方程(16)—(19)可以解出三轴应力张量的各个应力值.

3.3 实验结果

图5给出了SiCf/C/Ti17复合材料中基体α-Ti(213)高角衍射峰, 在ϕ =0◦,45◦,90◦三个方向测试的XRD图谱.采用高斯函数对每个峰进行拟合,算出每个dϕψ,并做出dϕψ与sin2ψ的图谱进行拟合,结果如图6所示. 在图6中,dϕψ与sin2ψ都显示出较好的线性关系,拟合得出kϕ=0◦ = −0.00103,kϕ=45◦ = −0.00091和kϕ=90◦= −0.00107.

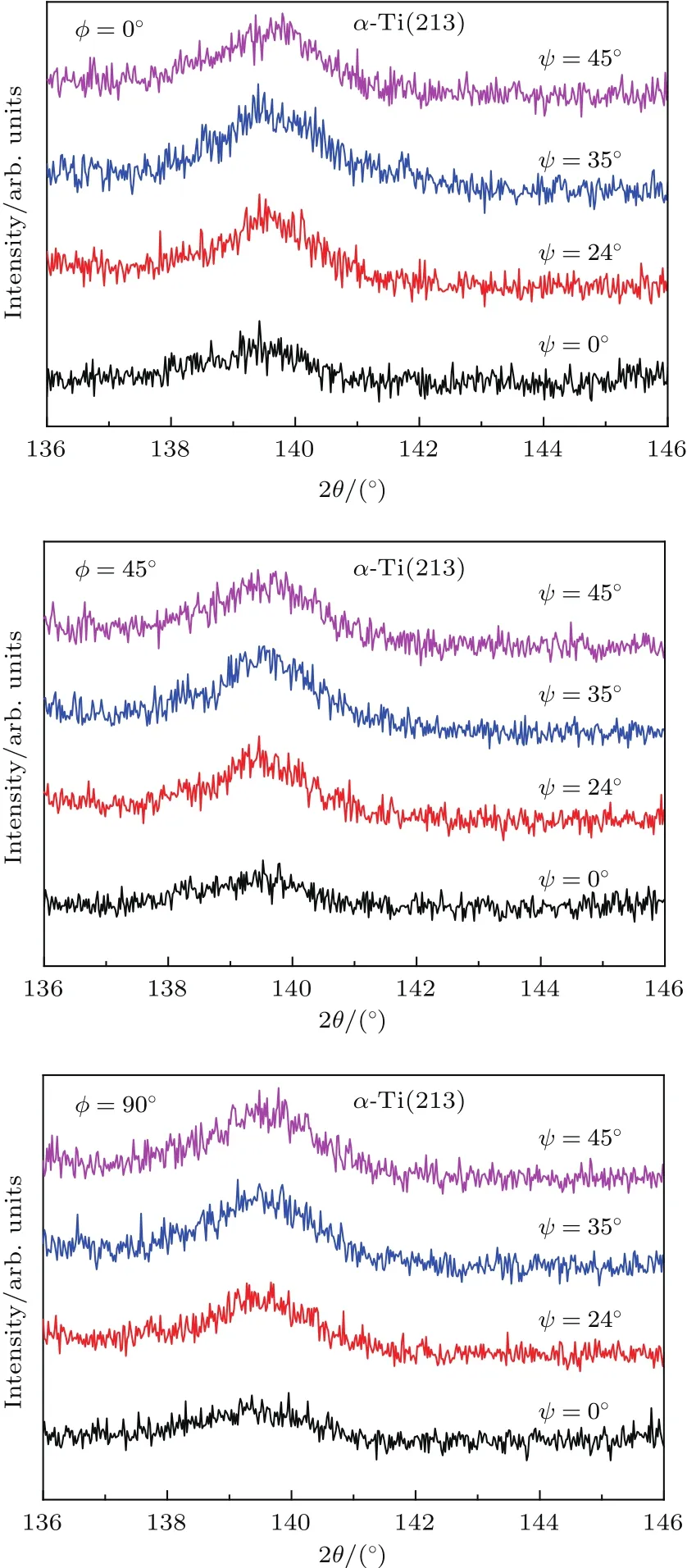
图5 在ϕ=0◦,45◦,90◦时改变ψ 的XRD图谱Fig.5.The XRD patterns measured at ϕ =0◦,45◦,90◦ with changing ψ.

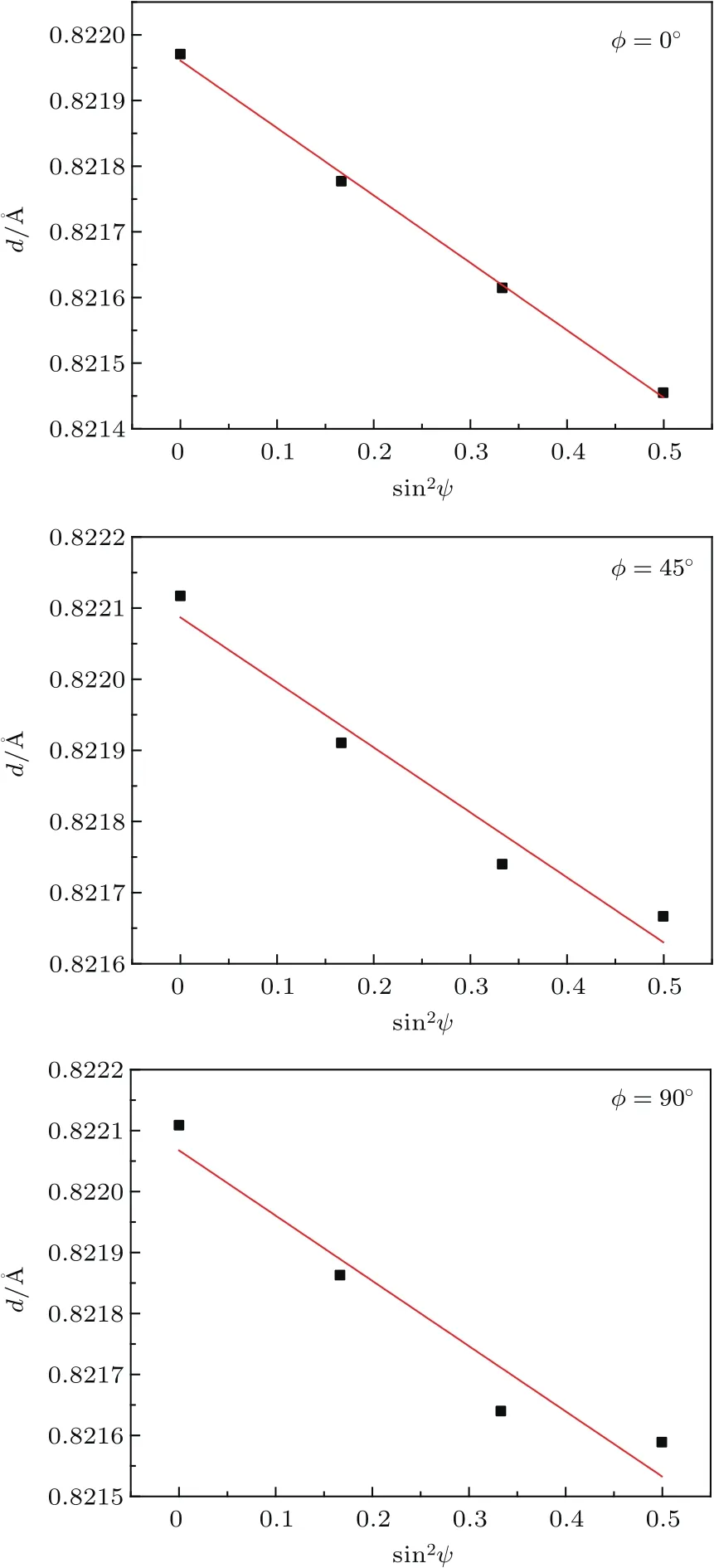
图6 在ϕ=0◦,45◦,90◦ 时的dϕψ-sin2ψ拟合图谱Fig.6.the fitting plots for dϕψ vs sin2 ψ at ϕ=0◦,45◦,90◦.

采用三轴应力模型,将kϕ=0◦= −0.00103,kϕ=45◦ = −0.00091,kϕ=90◦ = −0.00107和 在ψ=0时获得的平均截距¯dψ=0◦=0.82 Å代入方程(16)—(19),获得各应力值为σ11=474.7 MPa,σ12=130.5 MPa,σ22=465.9 MPa,σ33=701.3 MPa.此时,SiCf/C/Ti17复合材料内Ti17合金基体的轴向残余应力为σ33=701.3 MPa,呈现拉应力.由于纤维增强复合材料中,基体的轴向应力与SiC纤维达到平衡,即轴向应变由基体钛合金和纤维共同承担,通过线性弹性理论,轴向纤维应力与基体合金应力满足下式:

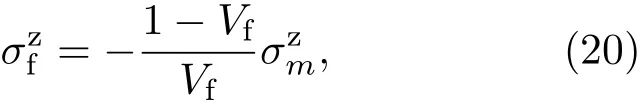
Vf为纤维体积含量48%,故X射线衍射法获得的SiC纤维的残余应力为−759.4 MPa,与拉曼光谱方法测量的值相当(−705.0 MPa),表明X射线衍射法中三轴应力模型能较好地分析处理纤维纵向排布的复合材料中的残余应力.

虽然上述两种测试方法都能对纤维增强复合材料的应力状态进行较为准确的测量与评价,但两种测试方法在原理和误差引入上存在巨大的不同.拉曼光谱法测试主要通过应变态下C涂层G峰的偏移来获得SiC纤维的应力,准确测量的前提是:1)C涂层具有高取向性和高的石墨化程度,保持石墨平面与纤维表面平行,这样能保证G峰对轴向应力比较敏感；2)由于拉曼的穿透深度较浅,高质量的表面能保持表面完全被钛合金包裹和束缚,进而更好地维持与内部相同的应力状态.而X射线衍射法主要测量基体钛合金的应变状态进而计算出应力状态,准确测量的前提为:1)获得准确的无应力态下基体钛合金的晶格常数,与复杂应力态下基体钛合金的晶格常数对比；2)与实际应力状态接近的分析模型如三轴应力模型,获得较为全面的应力状态；3)选取可鉴定和区分的基体钛合金的高角衍射峰进行测量.拉曼光谱法具有更简洁和快速的测量特征,但仅能获得轴向上的应力状态；相比之下,X射线衍射法测试分析更加复杂,但能获得更加全面的应力状态.

4 结 论

利用CVD的方法在SiC纤维单丝表面沉积了高织构的乱层石墨涂层,然后通过纤维涂层法制备了SiCf/C/Ti17复合材料,并分别采用拉曼光谱法和X射线衍射法获得了SiC纤维的残余应力.在拉曼光谱法测试中,根据无应力作用的C涂层和复合材料内有应力作用的C涂层的拉曼光谱图中G峰峰位的变化∆ω,计算得到SiC纤维在SiCf/C/Ti17复合材料内受到轴向压应力的作用,大小为705.0 MPa.基于三轴应力模型的X射线衍射法分析了纤维纵向排布复合材料中沿轴向方向的应力σ33,得到SiC纤维受到的压应力为759.4 MPa.两种方法获得的应力值相近,SiC纤维均受到压应力的作用,表明拉曼光谱法和X射线衍射法均可以较准确地测量SiCf/C/Ti17复合材料的残余应力.