托卡马克离子温度梯度湍流输运同位素定标修正中杂质的影响∗

沈勇 董家齐 徐红兵

1)(核工业西南物理研究院,成都 610041)

2)(浙江大学聚变理论与模拟中心,杭州 310013)

(2018年4月16日收到；2018年7月18日收到修改稿)

1 引 言

托卡马克放电的工作气体可以为氢,也可以是氢的同位素氘、氚,或者是氘-氘或氘-氚等混和气体.在不同托卡马克多种实验条件下,等离子体能量约束时间随主离子质量的不同变化很大[1−5].实验中观察到氢等离子体的约束性能较差,氘等离子体约束时间比氢等离子提高约40%左右,而氚等离子体的约束性能比氢等离子体提高70%左右.这种在氢类同位素等离子体中约束时间对工作气体正离子质量的依赖性,称为同位素质量依赖,是同位素效应的表现形式.在归纳同位素经验定标关系时,有时单独讨论同位素质量(Ai,可以是主离子质量数Mi或有效质量数Mfi)依赖(,有时既讨论质量依赖,同时还需给出有效电荷Zfi,效应,具体情况视研究对象而定.在不同装置上,或同一装置不同参数条件下,由实验数据得出的经验定标律[6−10]的不一致性非常突出,这是一个值得关注的现象.例如,Yushmanov等[6]对ITER L模能量约束数据库进行了研究,综合各种数据分析,得出能拟合数据库中大多数数据集的能量约束时间定标为τE∝A0i.5,与一些装置条件[7]下得到的经验定标结果一致.1978年,Hugill和Shfiield[8]在托卡马克典型的电子温度剖面即剖面为峰化的状态下得出的同位素效应经验定标关系为.如考虑在大多数实验条例下,Ti0/Te0≪1,则有Bessenrodt等[5]总结ASDEX碳化壁条件下的多种定标形式,较低密度放电和较高密度放电的定标一般情况(我们称之为“标准”情况)下,L模同位素定标∼在H模边缘输运垒处也具有这样的特征[9].总的而言,H模的同位素效应与L模是类似的[10].因此,本文研究L模放电情况[11].

如何从理论上解释托卡马克经验定标律中同位素定标关系的不一致性,即理解不同装置或不同参数条件下的定标律在“标准”(平均)定标指数0.5的基础上的“修正”,是优化聚变实验设计、提高等离子体能量约束、粒子约束和动量约束时间的一项重要课题.考虑到反常输运[12−14]对托卡马克等离子体能量约束的重要影响,许多研究者[15−20]从反常输运的角度,数值模拟研究同位素效应.重点是低频漂移模(包括ITG模和俘获电子模(TEM))湍流输运[21−24]的同位素效应及其定标关系[25−26].Dong等[16]和Tokar等[17]最先应用改进的混和长度估计方法(improved mixing length approximation,IMLA)[18]来进行这方面的理论模拟研究.我们在文献[20]中应用IMLA方法,研究了有钨杂质等离子体[27,28]ITG湍流输运的同位素效应,研究结果提供了很多信息,为从理论上探究托卡马克约束定标律的变化规律提供了有价值的信息.该项工作可以部分解释托卡马克同位素定标律的不一致性.但是,在文献[20]中ITG湍流输运同位素定标采用的是有效质量数作定标基础,依据是杂质效应对ITG模的作用体现在等离子体平均质量数的改变上,这在理论上是成立的；但从与实验完全匹配的角度看,其结果的充分性还稍嫌不足.因为不少实验对ITG模主导的湍流输运的同位素定标常常直接采用主离子质量数作为定标基础.例如,ASDEX观察得出的能量约束定标为(Mi/Zfi)2/5[5],Coppi[29]也从理论上导出了与之相符合的公式.因此,有必要更多地考虑实验定标的需求,采用与大多数实验一致的定标方式来完善该项研究.这是本文工作的动机所在.而对于杂质模,Coppi曾提出,当工作气体主离子由氢换成氘时,杂质模的不稳定性窗口将被展宽,从而降低约束时间.这与文献[20]的结果一致.而Dominguez[30]对氢和氘放电的准线性分析得到相应的杂质模湍流输运定标律是个结论是限定在低Zfi时得到的,结果与DIII-D实验观察接近,也与文献[20]的基本结论相符.但文献[20]没有详细分析杂质模同位素定标指数发生偏离的原因.本文在从有别于文献[20]的另一角度分析ITG湍流同位素效应的同时,对杂质模同位素效应也进行了详细分析,以得到有关理解ITG类(包括ITG和杂质模)湍流输运同位素定标修正中杂质所起作用的比较全面的结论.这是本文的目的所在.

本项工作研究含重(钨)杂质(可以有很宽的有效电荷数Zfi范围)等离子体离子温度梯度湍流同位素效应,可以看作是文献[20]的工作的拓展和完善.本文的主要成果一是确定了ITG湍流输运的另一种同位素定标关系,这种定标律的定标依据与实验经验定标方式相一致；二是从有别于文献[20]的另一个角度,揭示了重杂质注入后,同位素质量依赖和有效电荷效应与公认传统定标律τE∝的偏离趋势.本文对这种偏离现象做出了理论上的解释.这些结果与文献[20]的工作相互映证,揭示了托卡马克定标公式常常出现大的差异的原因.这项研究对托卡马克实验运行分析和对杂质相关的输运研究具有理论意义.

2 理论模型和方法

考虑具有圆截面的托卡马克环形位形.我们扩展低频漂移波回旋动理学积分方程[31],以便研究包含了杂质贡献的低频漂移模.保留离子的动理学特征量,如朗道共振、磁漂移和有限拉莫尔半径等.为简化起见,假定通行电子是绝热的,并忽略俘获电子的有限拉莫尔半径效应.非均匀等离子体中的低频静电扰动的动力学,用准中性条件=+Z来描述,其中,Z表示杂质离子的电荷数.

电子密度扰动(˜ne)、主离子扰动密度(˜ni)和杂质离子扰动密度(˜nz)分别为

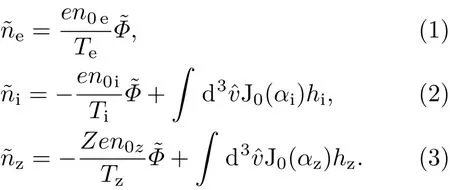
其中,若用s代表主离子i和杂质离子z,则αs=(2Ti/mi)1/2是正离子(主离子i或杂质离子z)热速度,离子回旋频率Ωs=qsB/cms.J0(αs)是零阶贝塞尔函数.正离子非绝热响应hs由下列方程确定:

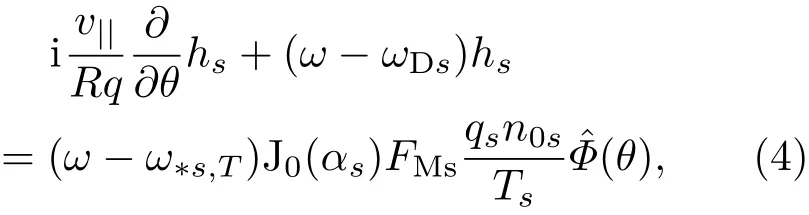
其中,

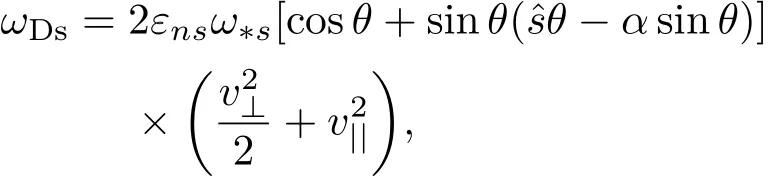
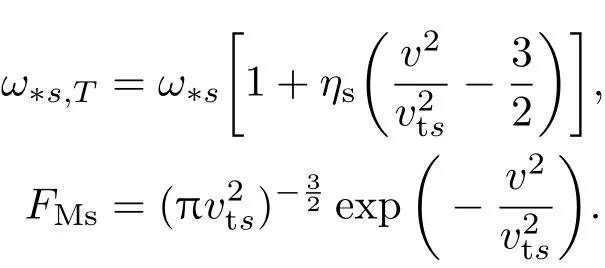
方程(4)是在假定圆截面s-α平衡模型下,根据气球模表象描述推导得来的.

根据准中性条件,由(1)—(4)式,可以得到包含杂质效应的积分特征值方程:

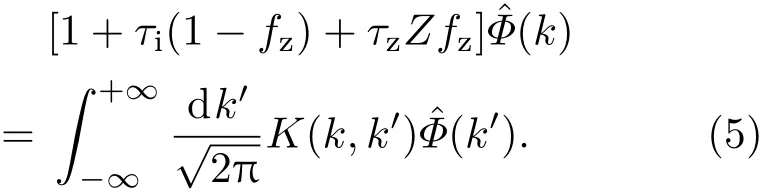
方程(5)的核为

Lns= −(d lnns/dr)−1(s=e,i,z)是密度梯度定标长度,e,i,z分别表示电子、主离子和杂质离子.模频率归一化到电子抗磁漂移频率ω∗e=ckθTe/eBLne, 波数k,k′和kθ归一化到意义表达,例如,LTs表示温度定标长度,q表示安全因子,sˆ=rdq/qdr是磁剪切.Ij(j=0,1)为j阶改进贝塞尔函数.此外,mu和Tu(u=i,z)表示离子质量和温度.

本文将求解积分方程(5),通过扫描归一化极向波数kθρH,求出ITG和杂质模的线性增长率和实频率,作为分析同位素效应和推算定标关系的源数据.根据托卡马克运行条件,除非另有说明,我们都选取如下基础参数:ˆs=1,q=2.5,εn=0.3,Te/Ti=Te/Tz=1.同时,为研究ITG模,取参数:ηi=ηe=3.9,Lez=1；为研究杂质模(IM),取参数:ηi=ηe=0,Lez=−2.这样选择参数是基于如下考虑:研究ITG模时,取Lez=1＞0,表明杂质密度剖面峰化方向与电子密度和主离子密度剖面峰化方向一致,同时,取较大的ηi=3.9,以确保研究的对象是典型的ITG模.反之,杂质模的驱动条件要求杂质密度剖面峰化方向与电子密度和主离子密度剖面峰化方向相反,即Lez＜0.故研究杂质模时,取Lez=−2；同时取ηi=0,以滤除ITG模特征,确保所研究的对象是完全的、典型的杂质模.

在同位素定标分析中需要用到对模最大线性增长率的拟合计算.拟合原则有别于文献[20].在文献[20]中,分析有杂质时的ITG模同位素定标关系时,使用的是有效质量数进行定标拟合.在本文中,ITG湍流同位素效应采用主离子质量数Mi进行拟合.对杂质模同位素定标,也采用主离子质量数Mi进行拟合,辅以有效电荷效应定标分析.

3 结果与讨论

通过选取不同等离子体参数,求解积分色散方程(5),结果用于分析ITG和杂质模湍流同位素效应及其定标关系.

3.1 ITG湍流同位素效应

图1给出了ITG模归一化增长率和实频率随归一化极向波数kθρH的变化曲线.杂质为W+13.其中,图1(b)所示实频率表明模的旋转方向在离子抗磁漂移方向,证明模属于ITG模.图1(a)表明,fz越大,最大增长率越小,谱宽越窄.可见,fz(从而杂质浓度)越大,ITG模增长度越小,说明杂质对ITG模的抑制作用越强.

从图1(a)可以明显看出ITG模的同位素效应.很明显,H+(D+)等离子体中ITG模最大增长率和谱宽都远远高于D+(T+)等离子体.下面我们对这种效应进行定量分析.图2示出了ITG模最大增长率关于主离子质量数Mi的拟合分析曲线.

图2从上到下的曲线对应的是fz逐渐增大的定标拟合曲线.红线、蓝线和黑线分别代表W+13,W+30和W+63杂质事例.可以看出,随着fz的增大,曲线变得越来越平坦,说明随着fz的增加,同位素质量依赖越来越弱.原因是在fz增加时,ITG线性增长率急剧降低,特别是,H+等离子体中的ITG相对D+,T+等离子体,D+等离子体相对T+等离子体的ITG模线性增长率的降低相对更快.这也说明H+等离子体中杂质对ITG模的致稳作用略强于D+,T+等离子体.

表1列出了ITG模最大线性增长率关于主离子质量数Mi的拟合结果数据.

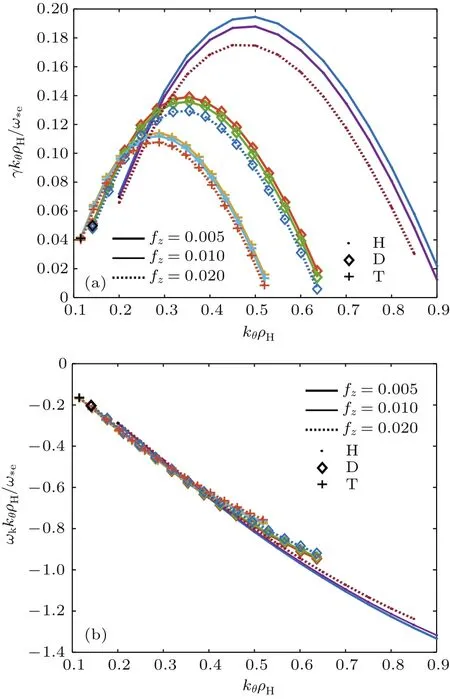
图1 (a)ITG模归一化增长率随归一化极向波数kθρH的变化曲线；(b)归一化实频率变化曲线；杂质为W+13Fig.1.The normalized growth rates(a)and real frequencies(b)of ITG mode in the presence of W+13 impurities.

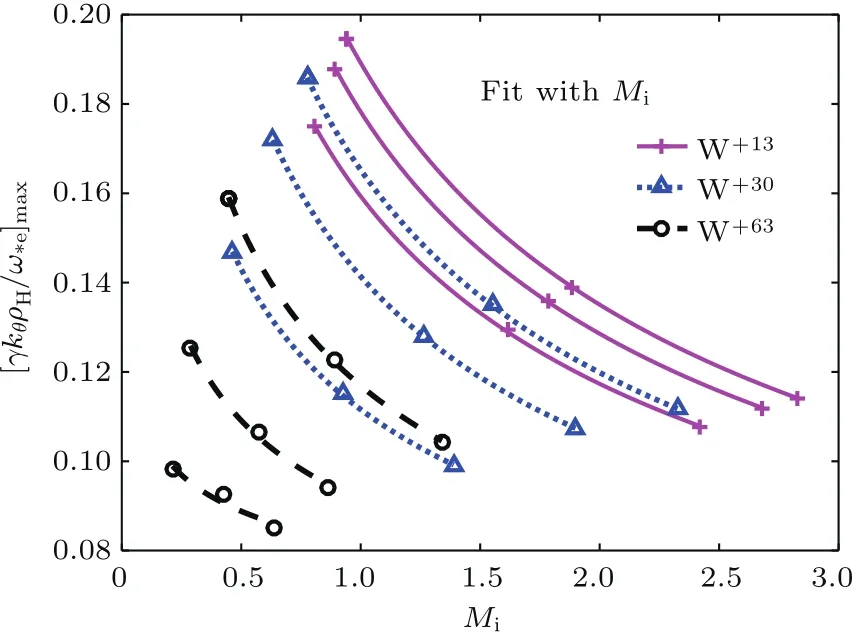
图2 有钨杂质等离子体ITG模最大增长率关于Mi的拟合曲线 红实线、蓝点线和黑虚线分别代表W+13,W+30和W+63杂质事例,每种事例从上到下的曲线表示fz逐渐增大时的拟合结果Fig.2.the fitting curves of the maximum growth rates of ITG modes with tungsten impurities.The curves from top to bottom correspond to the fitting results in the cases with increasing fzwith W+13(red solid lines),W+30(blue dotted lines)and W+63(dark dashed lines)impurities.

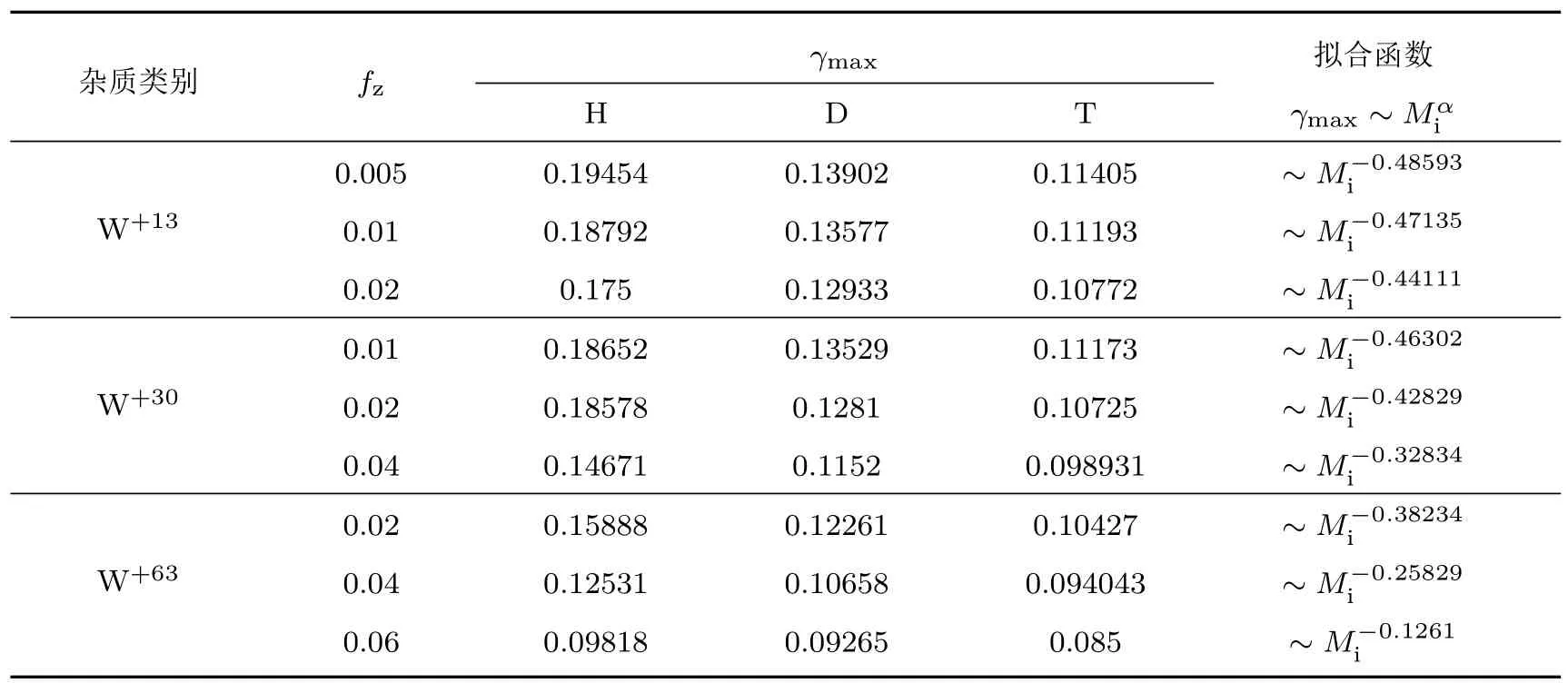
表1 ITG模最大线性增长率关于主离子质量数Mi的拟合结果Table 1.the fitting results of the maximum growth rates of ITG modes with primary ion mass number Mi.

表1表明,关于Mi拟合关系随Zfi的不同而有较大变化:Zfi越小,拟合指数越接近−0.5；Zfi越大,拟合指数越远离−0.5,最小处是W+63杂质、fz=0.06事例,Zfi=4.72,拟合指数为−0.1261.当杂质电荷集中度低时,如fz=0.005—0.025时,W+13与W+30两事例的拟合指数基本相同,都为α∼−0.45,如考虑等离子体中其他因素的影响,实际可取拟合指数为α接近−0.5.说明此处拟合指数与轻杂质的杂质模的定标指数[16]相同,与ITG模的Mfi定标系数相当.但是,当fz增大时,拟合指数α逐渐减小,说明同位素效应随杂质浓度的增加而减弱.特别是当fz很大且继续增加时,α值减小量急剧上升.例如,对于W+63质等离子体,fz=0.04时,α= −0.25829；当fz增加到0.06时,α=−0.1261,减小了将近一半.说明高浓度杂质等离子体同位素效应很弱,定标指数远远偏离−0.5.这是个很有实验和理论意义的问题.它表象上与不同种类等离子体中ITG的线性增长率降低的快慢有关,物理上是由于杂质对等离子体主离子的稀释作用,导致有效电荷数增加,同位素效应减弱.详细分析参见本文第4节.

3.2 含钨杂质等离子体杂质模同位素效应

杂质模同位素定标已在文献[20]中做了研究.在本文中其基本结论仍然适用.除此之外,钨杂质驱动杂质模的其他重要性质也值得考虑.

图3 (a)杂质模归一化增长率随归一化极向波数kθρH的变化曲线,杂质为W+46；(b)从上到下的曲线对应的是fz逐渐增大的Mi(主离子质量数)拟合曲线,红线、蓝线和黑线分别代表W+27,W+46和W+63杂质事例Fig.3. (a)The normalized growth rates of impurity mode(IM)with W+46impurities；(b)the fitting curves of the maximum linear growth rates of tungsten impurity modes with primary ion mass number Mi,the curves from top to bottom correspond to the fitting results in the cases with increasing fzwith W+27(blue dashed lines),W+46(red dotted lines)and W+63(dark solid lines)impurities.

图3(a)示出杂质为W+46时杂质模归一化增长率随归一化极向波数kθρH的变化曲线.对比图1(a)与图3(a)可见,相比ITG模,杂质模谱宽增加了很多,达ITG的3倍谱宽.但杂质模的线性增长率比ITG模要低得多.同时,fz越大,最大增长率越大,但相同等离子体对应的模谱宽基本不变,这与ITG模是不同的.从实验观察的角度,杂质模的这种宽谱特性是有利于观察的.但其低增长率说明它对等离子体的影响要小于ITG模.当然,很明显,当fz小到低于某个阈值时,模将被稳定化.杂质模不稳定性的充分显露,似乎需要fz越大越好,但实际上,等离子体中的杂质浓度是控制在一定范围内的,以使放电能继续进行下去.太高的fz是不现实的.至于杂质电荷数Z,当fz相同时,Z越大,即电离度越高,则线性增长率越大,谱宽也有小幅增加.

最重要的是,杂质模的同位素效应仍然是明显的.这从H+(D+)等离子体中钨杂质模最大增长率和谱宽都远远高于D+(T+)等离子体这两点,就可以直观地看出来.

图3(b)给出了钨杂质条件下杂质模最大增长率拟合曲线.可以看出,电离度(Z)越低,Mi拟合曲线越平坦.其中,W+27对应的曲线组最平坦,而W+63相关曲线组最陡峭.说明fz相同时,杂质电荷数Z越大,同位素效应越强.例如,在这里,W+27同位素效应最弱,而W+63同位素效应最强.

4 同位素定标关系偏离现象分析

上述模拟结果总结在表2和表3中.表2和表3分别列出了ITG和杂质模关于主离子质量数和有效电荷数的拟合结果,对应的拟合指数分别用α和β进行定量表示.

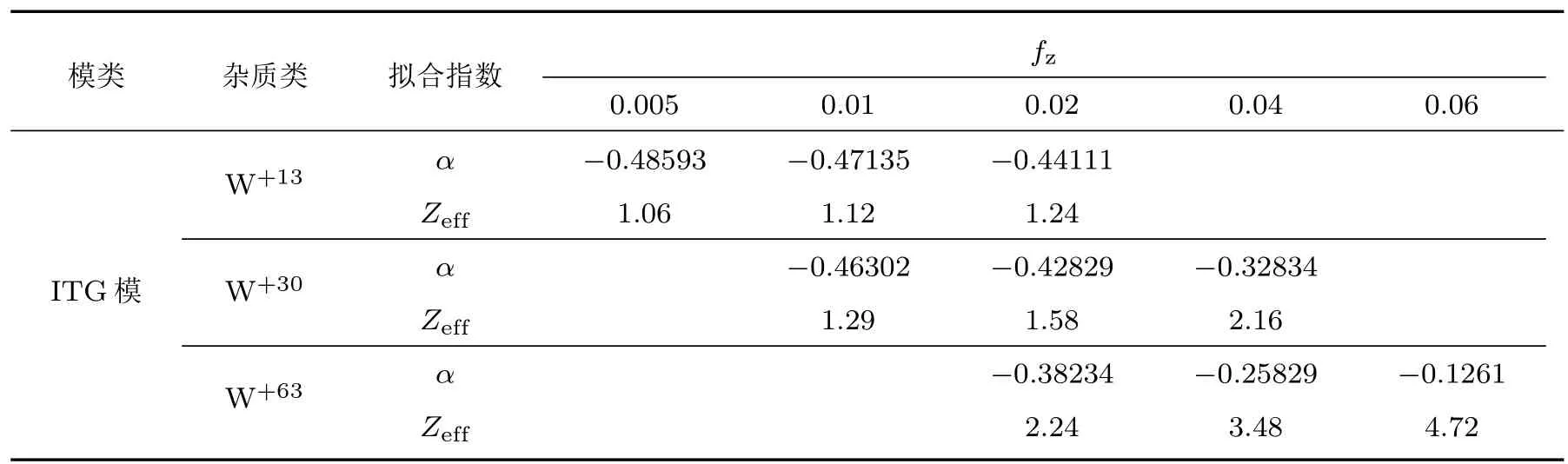
表2 ITG模关于主离子质量数Mi的拟合结果Table 2.the fitting results of ITG modes with primary ion mass number Mi.

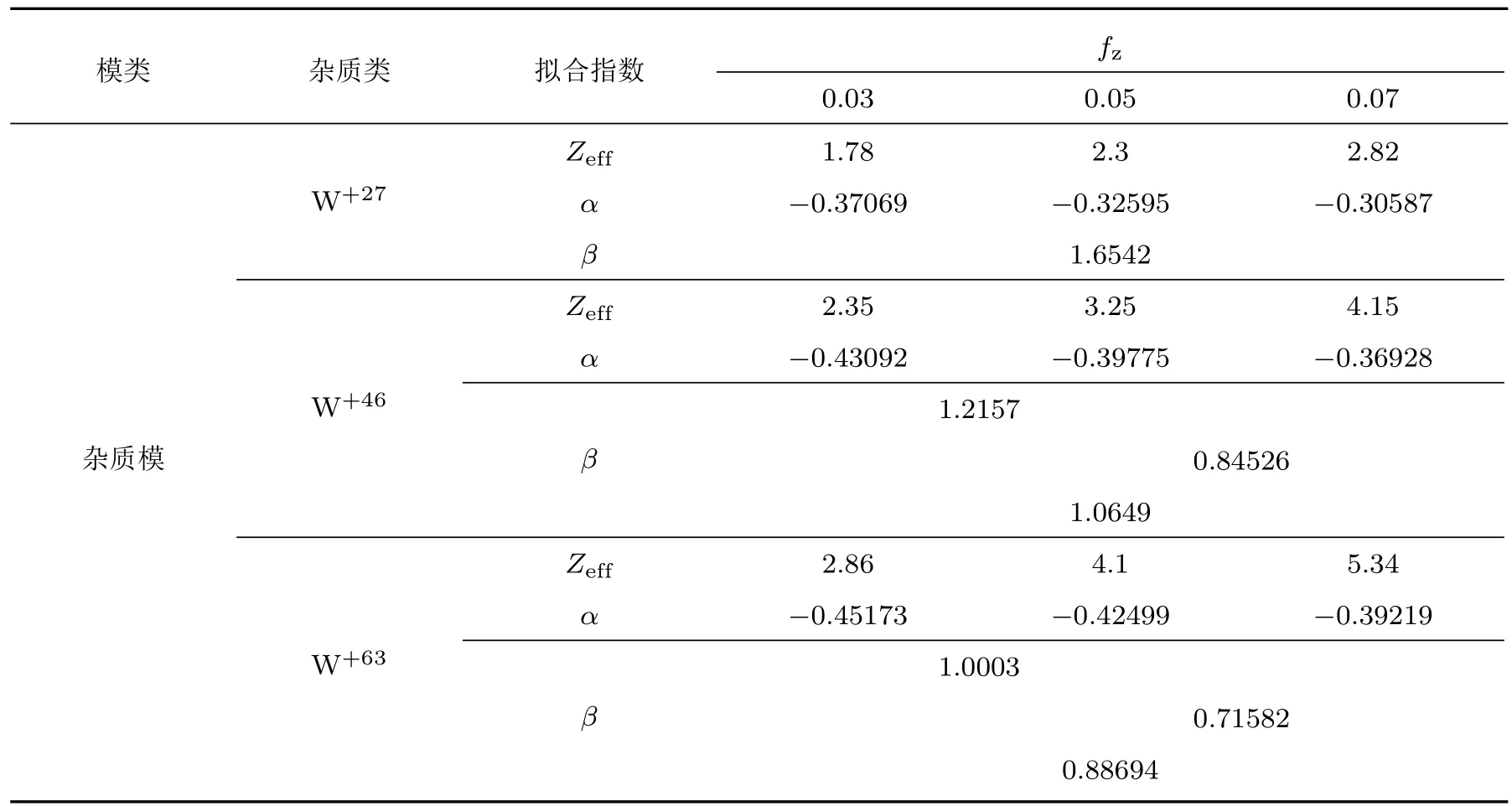
表3 杂质模关于主离子质量数Mi和有效电荷数Zfi的拟合结果Table 3.the fitting results of impurity modes with primary ion mass number Miand effective charge number Zfi.

表2和表3结果显示,在合理的电荷集中度内,求解积分方程(5)所得模拟ITG模最大增长率定标为有如下性质:有效电荷数Zfi越小,拟合指数α越接近−0.5.而杂质模的定标则不能直接从Zfi的大小确定同位素质量依赖定标指数的大小.具体情况是:其一,fz相同时,杂质电荷数越大,α越接近−0.5,否则,Z越小,则α偏离−0.5越远；其二,有效电荷效应规律是明确的,即有效电荷数Zfi越小,拟合指数β越大,反之,Zfi越大,则β越小.平均而言,在低Zfi(6 3)时,杂质模同位素定标时,杂质模同位素定标

在文献[5,29,30]中给出的ITG湍流同位素定标关系是τE∼ M,杂质模湍流定标为τE∼Z.前者与ASDEX实验观察一致,后者与DIII-D实验观察接近,而与ASDEX观察相抵触.说明不同托卡马克同一类型湍流输运可能存在不一致的定标规律.表2和表3所列模拟结果与上述经验定标律定性类同,不过其拟合指数α和β随等离子体具体参数在一定范围内波动,一般情况下,α相对于公认的“标准(平均)”定标指数即α=−0.5有一定程度的偏离(修正).特别是fz或Z较大时,偏离现象很严重.具体分析如下.

从色散方程(5)中可以清楚地看到,杂质电荷集中度fz和电度度Z对模的性质有显著影响.该方程不能解析求解,只能数值求解.从数值模拟结果可以明显看出fz和Z对同位素效应的影响.体现在两种模中,Z相同时,fz越大,拟合指数α偏离−0.5越远,相应同位素质量依赖越弱.关于有效电荷效应,杂质模的为γmax∼Z,随Z的增加,拟合指数在快速减小.可见,重杂质(钨杂质)效应使这两种低频漂移模的同位素质量依赖和有效电荷效应都有了很大改变.另一方面,fz相同而Z越大时,对ITG模(Lez＞0)拟合指数α偏离−0.5越远,而对杂质模(Lez＜0)则相反,α越接近−0.5.这可以分别解释如下.对杂质模,由于模主要由杂质密度度梯度驱动,杂质数越多,杂质对等离子体微观不稳定性的影响越显著,导致拟合指数与正常定标系数的偏离.然而,ITG模主要由主离子温度梯度驱动,杂质的出现只对ITG模起致稳定作用(当Lez＞0).杂质数量越多,其对主离子为较轻粒子的等离子体(如H+等离子体)中ITG模的致稳定作用要强于较重的主离子,如D+,T+等离子体,即有杂质效应引起的线性增长率变化∆γmax,H＜ ∆γmax,D＜ ∆γmax,T,其原因是:H+等离子体中有效质量数Mfi=(1−fz)MH+fzMw,杂质占比相比于D+,T+等离子体来说更大,fz相同时,Mfi相等,当电离度越高即Z越小时,相对于D+(或T+)等离子体,在H+(或D+)等离子体中ITG模不稳定性越不容易受到杂质作用的抑制,从而拟合指数α就越大.反之,当fz相同而Z越大时,即对应的杂质数量越少时,杂质效应引起线性增长率变化有如下关系成立:∆γmax,H＞∆γmax,D＞∆γmax,T,从而指数α就越小.

对于Z相同,fz越大意味着杂质数量越多,这时α会越偏离−0.5,原因是有效质量数Mfi随fz的增加而急剧增大了.事实上,fz和Z增大,意味着有效电荷数Zfi增加,在实验上对应于低密度,同位素质量依赖会减弱,表现为Mi拟合指数α数量上大于−0.5(|α|＜0.5),并且,随着Zfi增加,这种数量上的偏离越来越远.

对于杂质模,当纯杂质浓度(=fz/Zc)增加时,当Zc不变而fz增加,或者fz不变而Zc减小时,拟合指数α都在减小,表明同位素质量依赖在减小.杂质模拟合指数α减小时,关于Zfi的拟合指数β却在上升,表明有效电荷效应增强.上述两个现象说明,杂质模同位素效应在各参数域内都有较强的表现.因此,其对粒子输运和热输运的影响是不可忽视的.然而,对于ITG模,fz的影响可分为两方面.一是对于相同电离度的杂质,即Z不变时,当fz增加,纯杂质浓度增加,同位素效应越来越弱,主要是质量依赖在减弱；而当fz不变而Z减小时,同样意味着纯杂质浓度增加,α也在增加,说明同位素质量依赖在增强.上述性质恰好说明了重(钨)杂质效应显著修改了ITG模的同位素效应.

等离子体同位素质量依赖和电荷效应会随杂质种类、浓度和杂质电荷数的变化而发生显著变化,这一结果与文献[20]的结论是符合的.但本文有关ITG模湍流同位素效应定标关系的分析,展示出随Zfi的增加,同位素质量依赖有减弱的趋势.这在形式上与文献[20]的结果部分不符.文献[20]指出,随fz或Z的增加,ITG模有效质量数的依赖关系表现为增强趋势.这是由于定标基础不同所引起的.定标形式直接包含了对同位素质量Mi的依赖关系,而M定标形式包含了主离子质量数Mi、杂质浓度fz和杂质电离度Z三者的贡献,此定标形式不能直接反映主离子质量依赖关系.fz或Z增加时,ITG湍流输运对有效质量数的依赖关系的增强主要是杂质的贡献,因为杂质质量Mz相较于氢同位素质量数相对太大.

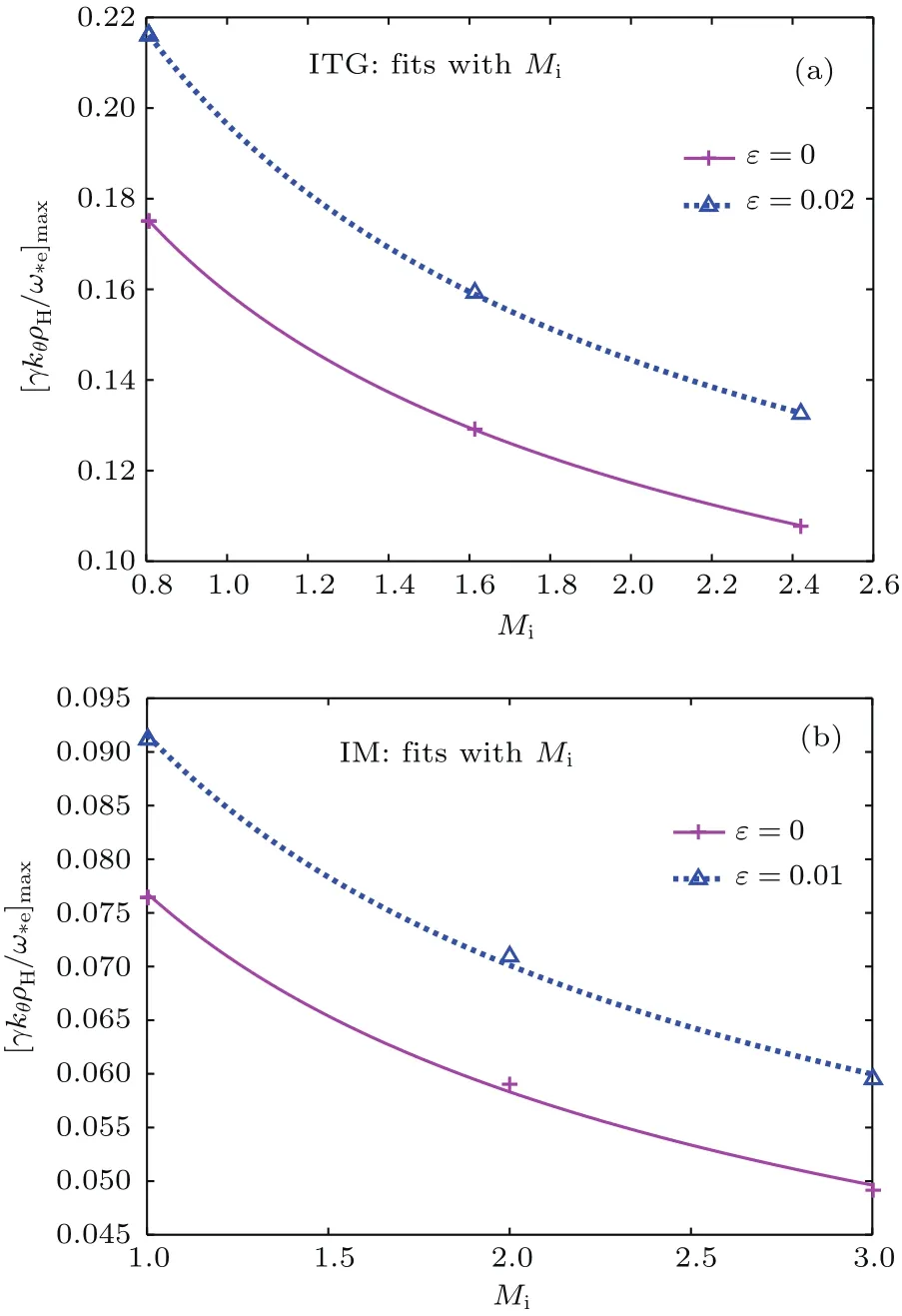
图4 电子非绝热效应的影响示意图 (a)ε=0和0.02时,ITG模最大增长率关于Mi的拟合曲线,杂质为W+13；(b)ε=0和0.01时,杂质模最大增长率关于Mi的拟合曲线,杂质为W+46Fig.4.The effects of electron non-adiabatic response:(a)the fitting results with Miof maximum growth rates of ITG modes in the cases of ε=0 and 0.02；(b)the fitting results with Miof maximum growth rates of IMs in the cases of ε=0 and 0.02.

本文的研究工作及结论是在假定电子响应为绝热响应的情况下做出的.为讨论该结论的适用范围,我们同时研究了加入非绝热电子的情况.在方程(5)右端,加上非绝热电子响应项[19]:

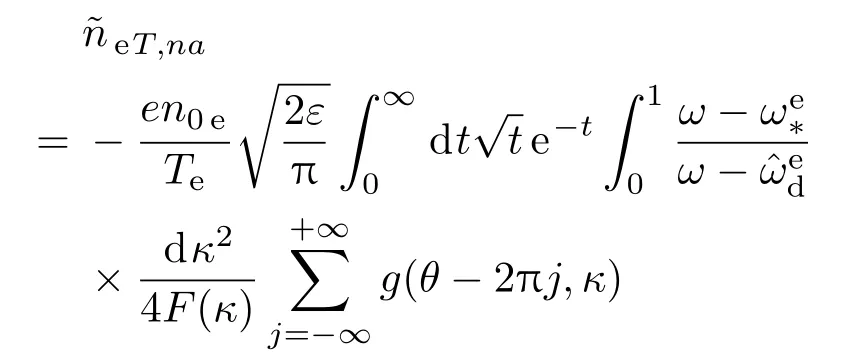
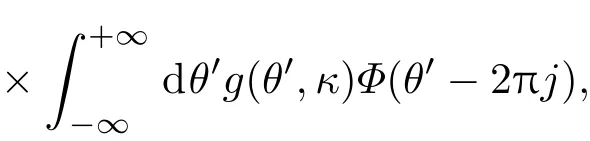
求解新的方程(5),可得包含俘获电子效应的ITG/IM数值结果.图4中给出了包含俘获电子效应前后的结果对比示意图.图中红色曲线是本文采用的假定电子响应为绝热的情况,蓝色点线为考虑了俘获电子效应(非绝热响应的一种)的情况.从图4可以看出,考虑俘获电子效应后,ITG和杂质模的最大增长率都有了较大增加,说明模被去稳定化了.但是,关于同位素质量依赖的拟合曲线基本一致.事实上,从表4所给出的拟合数量结果可以更清楚地看到这一点.

显然,考虑俘获电子效应时,并不改变本文关于ITG/IM不稳定性同位素定标规律的基本结论.同时,考虑ITG湍流的非线性与非局域化特征时,也不会影响本文的结论,在此不做详细讨论.

事实上,有多种模型可以解释实验上观察到的同位素效应.根据IMLA理论[16−18],热扩散系数D⊥∼γL∆r∼(γL/k2⊥)maxk⊥,当假定扰动的径向相关长度∆r与离子拉莫尔半径无关时,径向相关长度独立于单一谐波,则用绝热电子响应条件下的线性模拟方法,就可以利用ITG模线性增长率随同位素质量的增加而定量减小的性质,来解释约束时间(τE∼ 1/D⊥)的质量定标律.因此,本文的结论适用于ITG湍流占主导的反常输运分析.

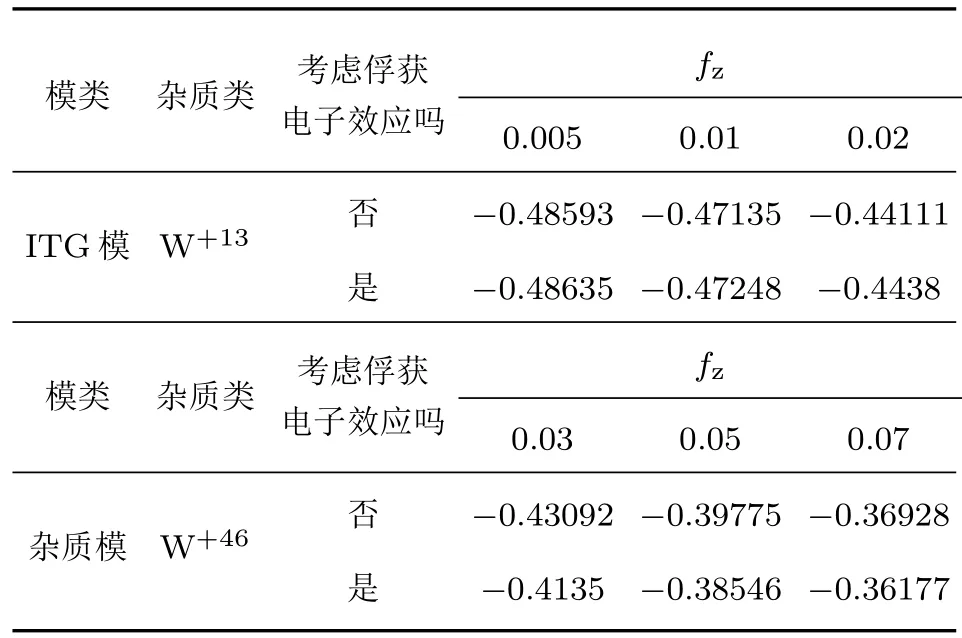
表4 考虑与不考虑俘获电子效应时,ITG和杂质模的同位素质量依赖拟合指数α值的对比Table 4.The comparison of the fitting index α about isotope mass dependence of ITG and impurity modes with or without consideration of trapped electron effects.

5 结 论

本文应用回旋动理学方法,通过求解含杂质等离子体低频漂移波色散方程,对含钨杂质等离子体ITG和杂质模湍流输运的同位素效应进行了数值研究.结果表明,钨杂质效应极大地修改了同位素定标律和有效电荷效应.随着杂质离子电荷数Z和电荷集中度fz的变化,同位素定标律在较大范围内变化.ITG模最大增长率定标大约为同特征是,当杂质电荷集中度增加时,同位素质量依赖减弱.另外,对ITG模而言,有效电荷数Zfi的增加,可导致同位素质量依赖的减弱.杂质模情况复杂一些.在电离度Z相同时,有效电荷数Zfi的增加,也可导致杂质模同位素质量依赖的减弱.杂质浓度相同时,有效电荷数Zfi的增加却导致同位素质量依赖的增强.平均来看,在低Zfi(6 3)时,杂质模同位素定标Zfi(＞3)时,杂质模同位素定标

本文的研究结果是对文献[20]工作的补充和拓展.相对于文献[20],本文更具体地研究了杂质效应使定标关系发生偏离的原因.概括地说,它是基于杂质种类、含量与电离度的不同,造成了同位素定标指数或小或大地偏离−0.5.这也是不同托卡马克上或同一装置不同参数条件下得到的等离子体同位素经验定标律有相当大差异的原因之一.由此可见,如同托卡马克实验经验定标[1−8]展示的那样,拘泥于过于精确的定标系数是没有意义的,但是研究在等离子体同位素质量依赖和有效电荷效应的大致的定标范围确实是可行的.ITG湍流输运是影响托卡马克等离子体约束性能的主要因素.本文对ITG湍流同位素效应的理解和定标,与实验事实相符.基于同位素效应研究的工作气体选择或其组合是改善约束性能、提高约束时间的手段之一.显然,在对ITER运行中的实验安排以及与杂质相关的输运实验研究中,这些结果可作为解决装置材料选取、工作气体选择和实验参数设置等技术问题的一个理论基础.