含磁电弹夹层的压电/压磁声子晶体带隙特性研究∗
孙炜海 张超群 鞠桂玲 潘晶雯
1)(陆军装甲兵学院车辆工程系,北京 100072)
2)(陆军装甲兵学院基础部,北京 100072)
(2018年5月9日收到;2018年8月18日收到修改稿)
1 引 言
近年来,随着人们对层状多铁性复合材料研究的深入,压电/压磁声子晶体在实际工程技术领域发挥了越来越重要的作用.与纯压电或纯压磁结构体系相比,压电/压磁复合结构可以实现机械能、磁能和电能三者之间的互相转换,同时因其具有声子晶体的带隙特性,成为制造谐振器元件、电场可调滤波器和磁场探针等一些高科技精密零件的理想材料[1−7].
由于压电和压磁材料的参数相差较大,压电/压磁声子晶体在使用过程中不同材料层交界处容易出现变形损伤[8,9],可以通过在不同材料交界处插入磁电弹夹层实现材料参数之间的平滑过渡.目前,磁电弹材料通常由压电和压磁材料粉末混合烧结而成,具有力电磁耦合功能,磁电弹夹层的引入会较大程度上影响压电/压磁声子晶体的力学、电学和磁学行为及其两两之间的耦合作用,从而既可能带来一些新的科学现象与机理,也可能引起压电/压磁器件的性能变化.从本质上来看,压电/压磁层状复合结构中电磁场方程与弹性动力学方程是耦合的,但是由于弹性波波速与电磁波波速相差超过4个数量级,因此可以忽略麦克斯韦电磁场方程中磁场与电场的耦合.在现有的研究成果中,大部分都采用了准静态近似条件.Qian等[10]研究了SH波在周期性压电复合材料结构中的传播.Pang等[11]研究了SH波在压电/压磁层状复合材料中传播的带隙特性.Lan和Wei[12]研究了梯度夹层对压电/压磁声子晶体带隙特性的影响.Liu等[13]研究了波在压电/压磁层状周期结构中的传播特性,讨论了复合材料各组分材料参数的差异对带隙特性的影响.Guo等[14]研究了初始应力对压电/压磁声子晶体色散关系的影响.Zhu等[15]研究了不同界面结合条件对压电/压磁声子晶体色散特性的影响.Wei等[16]研究了功能梯度层对层状压电/压磁圆柱体中剪切水平波频散关系的影响.Wang等[17−19]研究了二维压电/压磁与磁电弹性声子晶体中弹性波的传播.对含磁电弹夹层的压电/压磁声子晶体开展力学分析,不仅在理论研究方面具有重要的科学价值,而且在元件设计、制造和应用等方面具有重要的工程应用价值.目前含磁电弹夹层三组元声子晶体带隙特性的研究较少,需要进一步深入研究.
本文主要研究了在准静态电磁条件下,含磁电弹夹层的压电/压磁声子晶体带隙特性,用传递矩阵法和Bloch定理得到了声子晶体中SH波的色散关系,通过对色散方程进行数值求解,讨论磁电弹夹层的厚度、磁电弹夹层中压电材料的体积分数和磁电弹夹层中压电材料种类对压电/压磁声子晶体带隙中心频率和带隙宽度的影响.
2 理论分析
压电、压磁和磁电弹材料在高温高压条件下交替黏连成层状周期复合结构,如图1所示.压电层与压磁层厚度相同为d1,磁电弹层厚度为d2,单胞的总长为2a=d2+d1+d2+d1,层状周期复合结构沿x3轴极化,在x1-x2坐标平面各向同性.

图1 含磁电弹层的声子晶体模型Fig.1.Model of phononic crystal with MEE interlayer.
磁电弹材料的本构方程为

式中σ,s,D,E,B和H依次分别表示弹性应力张量、应变张量、电位移矢量、电场矢量、磁感应矢量和磁场矢量;c,ε和µ依次分别代表弹性系数、介电系数和磁导率张量;e,q和α依次为压电常数、压磁常数和磁电常数张量.当等式中q=α=0和e=α=0时,分别表示压电材料和压磁材料中的本构方程.
位移矢量u与应变矢量s之间关系为

其中,T表示转置,∇为哈密顿算子,上标J=e,m分别表示压电材料和压磁材料;电场矢量E与电势φ之间的关系为

磁场矢量H与磁势ϕ之间的关系为

准静态近似条件下,忽略体力、磁荷和自由电荷的存在,不考虑麦克斯韦电磁场方程中磁场与电场的耦合,则应力矢量σ、电位移矢量D和磁感应矢量B三者满足的平衡方程为

在考虑SH波的情况下,位移u3、电势φ、磁势ϕ是自变量(x1,x2)的函数.把等式(1),(2),(3)和(4)代入到等式(5)中,得到磁电弹材料的控制方程,根据q=α=0和e=α=0的两种情况,分别推导出压电和压磁材料的控制方程,利用Pang等[20]解控制方程的方法,可以得到位移u3、电势φ、磁势ϕ、应力σ31、电位移D和磁感应强度B在压电、压磁和磁电弹材料中的表达式.

其中,上标e′和e′′分别表示压电子层的左侧和右侧.
压电子层两侧向量满足以下关系:

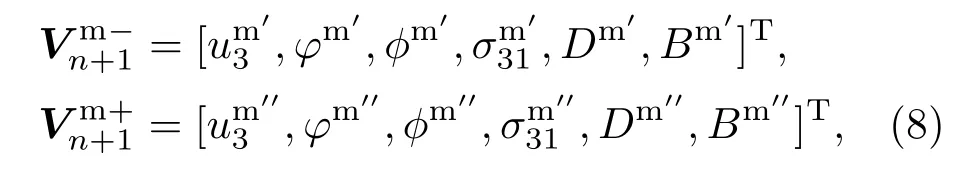
其中,上标m′和m′′分别表示压磁子层的左侧和右侧.
压磁子层两侧向量满足以下关系:
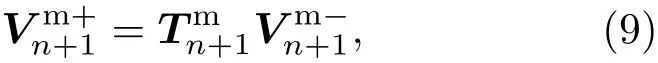
其中,上标mee′和mee′′分别表示磁电弹夹层的左侧和右侧.
磁电弹夹层两侧向量满足以下关系:

由压电子层、压磁子层和磁电弹夹层组成的单胞左右两侧的状态向量满足以下关系:

其中,Tcell为总体传递矩阵,可以表示为

同时,根据Bloch定理可得

其中,k是Bloch波波数.把(12)式代入(14)式得

(15)式中存在非零解的条件为
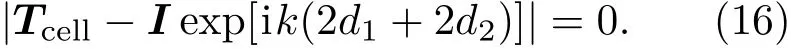
3 数值计算与分析
在每一个子层中,材料视为均质,磁电弹夹层材料参数取决于层板中压电材料和压磁材料的体积分数.其中满足Pmee=PeVe+PmVm,式中P为磁电弹夹层材料参数,Pe为压电材料各项参数,Pm为压磁材料各项参数,Ve为磁电弹夹层中压电材料的体积分数,Vm为磁电弹夹层中压磁材料的体积分数,其中Ve+Vm=1.虽然在压电和压磁材料中磁电系数α11=0,但是在磁电弹夹层材料中α11=4αmaxVeVm,其中αmax为α11的最大值,αmax=5×10−12Ns/VC.
在实际讨论计算中,单胞厚度取固定值0.004 m,则a=0.002 m,压电/压磁声子晶体中压电材料为BaTiO3,压磁材料为CoFe2O4,b为磁电弹夹层中压电材料占总材料的体积分数.讨论磁电弹夹层厚度对带隙特性的影响时,取b=0.5,磁电弹夹层中压电材料为BaTiO3,压磁材料为CoFe2O4.在讨论压电材料体积比的影响时,单胞厚度保持不变,为0.004 m.磁电弹夹层中压电材料为PZT-5A,压磁材料为CoFe2O4,磁电弹夹层厚度d2取定值0.001 m.在讨论压电材料种类的影响时,磁电弹夹层厚度d2=0.001 m,磁电弹夹层中压电材料占总材料的体积分数b=0.5.

表1 材料参数[21]Table 1.Material parameters[21].
当d2=0时,磁电弹夹层厚度为0,此时曲线为压电/压磁声子晶体色散曲线;当d2>0时,此时曲线表示的是三组元声子晶体中弹性波的频散关系.从图2可以看出,磁电弹夹层厚度d2的改变对第一带隙的宽度影响比较小,当d2从0增加到0.5a时,第一带隙宽度基本保持不变,仅由0.04增加到0.07,第一带隙中心频率由0.522上升到0.760.而对第二带隙和第三带隙影响比较大:第二带隙宽度明显变大,由0.001增加到1.12;第三带隙宽度略微变宽,由0.04增加到0.23;第二带隙中心频率由1.045上升到1.614,第三带隙中心频率从1.568增加到2.508.声子晶体中弹性波的带隙形成遵循Bragg散射机理,在增加磁电弹夹层后,改变了声子晶体周期结构,同时因磁电弹夹层的存在,不同子层各项参数之间的差值发生改变,使得SH波在声子晶体中传播的带隙特性也发生改变.随着磁电弹夹层厚度d2的增加,带隙宽度增加,带隙中心频率向高频方向移动.

图2 带隙随磁电弹夹层厚度的变化Fig.2.Band gap varying with thickness of MEE interlayer.
从图3可以看出,随体积分数b从0增大到1,第一带隙宽带隙中心频率由1.431下降到1.023,第一带隙宽度从0.652减小到0.358.通过图4可以得到,当b=0时,此时磁电弹夹层全为压磁材料,第二和第三带隙中心频率分别是2.614和4.163;当b=0.4时,第二和第三带隙中心频率分别是2.430和3.999;当b=1时,此时磁电弹夹层全为压电材料,第二和第三带隙中心频率分别是2.095和3.707.在b从0增加到1的过程中,第二带隙的宽度由0.853增加到1.053,第三带隙的宽度基本没变,保持在2.02左右.三个带隙的中心频率都随着压电材料所占总材料的体积分数b的增大向低频方向移动,但各个带隙宽度的变化不相同.通过分析计算可知,随着体积分数b的增大,磁电弹夹层中压电效应在增强,而压磁效应在减弱,各组分的材料参数差异发生改变;由于Bragg散射机理的作用,声子晶体带隙特性也发生改变.随着压电体积分数的增加,带隙中心频率向低频方向移动,中心频率越高,移动越明显,第一带隙宽度明显变窄,第二稍微变宽,第三带隙基本不变.
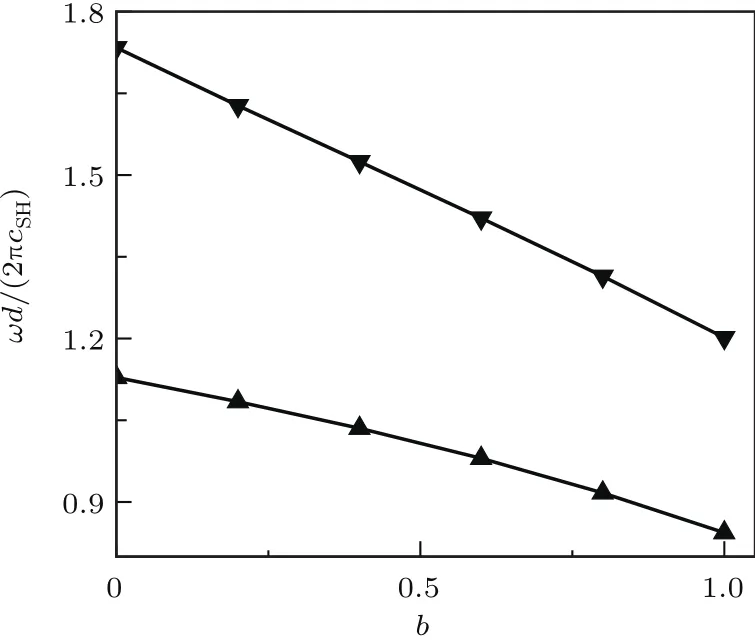
图3 压电材料体积分数对第一带隙特性的影响Fig.3.The influence of volumefraction of piezoelectric material on the first band gap characteristics.

图4 带隙随压电材料体积分数的变化Fig.4. Band gap varying with volumefraction of piezoelectric materials.
从图5可以看出,不同的压电材料对带隙的中心频率和带隙宽度有明显影响.由于各项材料参数的影响一直存在,需要将不同材料的带隙中心频率和带隙宽度与相对应的材料参数相比较.结果发现,压电材料弹性模量越大,声子晶体带隙中心频率越高,带隙宽度越宽.结合声子晶体带隙机理及带隙特性,可以得到弹性模量比其他材料参数对带隙变化影响更大,并且随着带隙所在区域频率的升高,带隙特性的变化越明显.
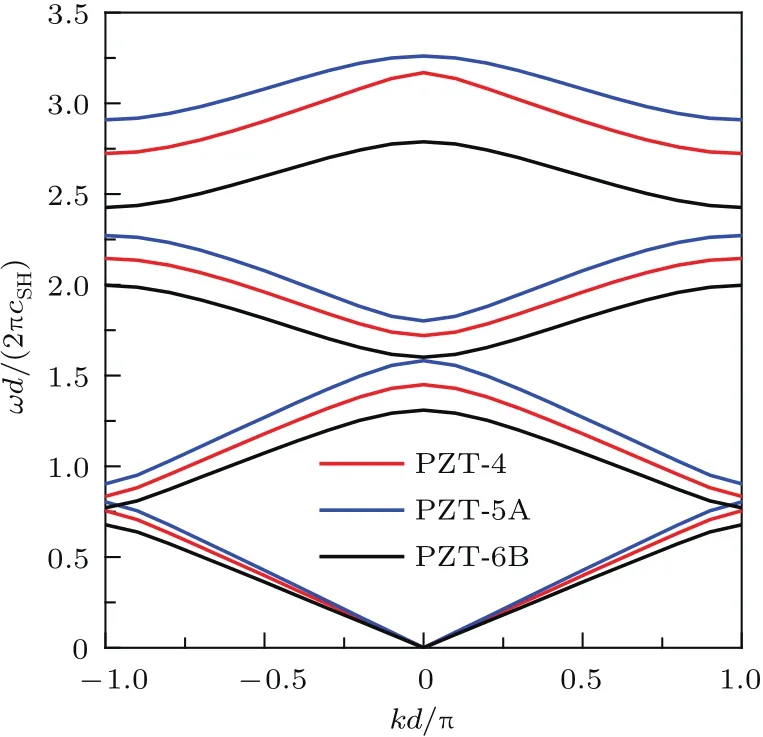
图5 压电材料不同时声子晶体的带隙Fig.5.Band gap of phononic crystal with different types piezoelectric material.
4 结 论
本文通过构建含磁电弹夹层的一维压电/压磁声子晶体模型,利用传递矩阵法和Bloch定理得到了模型中SH波的色散方程,并把方程的解以图像的形式展现出来,根据图像讨论磁电弹层对压电/压磁声子晶体带隙特性的影响.结果表明,插入的磁电弹夹层可以改变压电/压磁声子晶体带隙宽度和中心频率.当磁电弹层厚度增加时,带隙的中心频率上升,带隙宽度变宽;当磁电弹夹层中压电材料体积分数增加时,带隙中心频率下降,第一带隙宽度变窄,第二带隙宽度增加,第三带隙宽度保持不变;当磁电弹夹层中的压电材料种类不同时,带隙的中心频率和带隙宽度有明显的改变;磁电弹夹层对压电/压磁声子晶体带隙中心频率的影响在高频区比低频区更显著.因此,在设计声子晶体结构时,可以通过增加不同的磁电弹夹层,在一定程度上调节带隙的宽度和中心频率.

