为数学点赞——名师列析数学文化（8）数列

■北京市教育学院丰台分院 张 琦

■北京市第十二中学高中部 高慧明

本刊特邀栏目专家简介:

张 琦 北京教育学院丰台分院数学教研员,骨干教师,中国教育学会辅导机构教师专业水平等级认证专家评委、命题专家。主编《高考复习三级跳》丛书数学卷,在全国知名学术期刊上发表有影响的论文数十篇。

高慧明 首届全国十佳班主任,全国著名数学特级教师,国家教育部课程改革“全国先进工作者”,全国著名高考数学命题与考试研究专家,国家教育部“国培计划”全国中小学教师培训、班主任培训、校长培训特邀主讲专家,受邀在全国各地做有关高考科学备考、班级管理等多场专题报告。现任教于北京市第十二中学高中部。

《普通高中数学课程标准（2017年版）》要求高中数学要将“数学文化融入课程内容”,并进一步指出:“在教学活动中,教师应有意识地结合相应的教学内容,将数学文化渗透在日常教学中,引导学生了解数学的发展历程……”同时,课标特别指出“在教学中可以组织学生收集、阅读数列方面的研究成果,特别是我国古代的优秀研究成果,如杨辉三角、《四元玉鉴》等”。

《数列》这一章的教材中,涉及了很多生活、生产中的数学问题。无论在东方还是在西方,古往今来,数列始终是数学研究的重要问题之一,历史悠久,文化灿烂。

在古代中国,《庄子》中有“一尺之棰,日取其半,万世不竭”的说法,而《易经》也有云“是故《易》有太极,是生两仪;两仪生四象,四象生八卦”,这里都包含了数列的含义。在西方,传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,比如他们研究过1,3,6,10,…由于这些数都能够表示成三角形,他们就将其称为三角形数（如图1）。类似地,1,4,9,16,…被称为正方形数,因为这些数能够表示成正方形（如图2）。

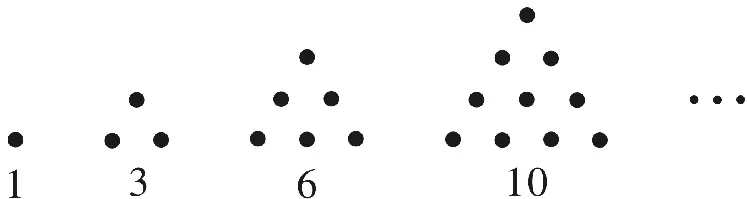
图1

图2

在人教版教材高中A版数学必修5第2章数列复习参考题A组中有这样一道选择题:

《莱因德纸草书》（Rhind Papyrus）是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给5个人,使每人所得成等差数列,且使较大的三份之和的是较小的两份之和,问最小的一份为（ ）。

这是一个“已知等差数列的项数n=5,前五项和S=100,以及a+a=（a+a51234+a5）,求a1”的问题。设公差为d,根据通项公式an=a1+（n-1）d以及前n项和公式得解。

本题中提到的莱因德纸草书是古埃及人用一种由纸莎草（Papyrus）压制成的草片集制而成的,最初发现于埃及底比斯古都废墟,1858年为苏格兰收藏家莱因德（H.Rhind）购得,因此得名。莱因德纸草书问题40即是:“五人按等差数列分100片面包,最少的两份之和是另外三份的七分之一。问:五人各得多少?”纸草书中的解答采用了假设法进行解答,设最小的一项为1,则以后各项依次为1+d,1+2d,1+3d,1+4d。于是有2+为60,而已知各项之和为100,因此,各项乘会发现,数列的历史悠久,有关数列话题古老,阿拉伯、古印度、中国古代、古希腊等的数学历史中都有数列的主题,分布广泛,人类对数列的认识很早,而且这些国家、地区对数列的认识也比较深入。下面我们就通过几个简单的例子进行阐述。

（一）古巴比伦人的数学智慧

考古学研究表明,古巴比伦人当时使用的是特殊的楔形文字,并把文字刻在泥板上晒干,晒干后的泥板变得和石头一样坚硬,可以长期保存;但岁月的侵蚀还是使得大部分泥板书消磨破损,保存下来的泥板书数量远不及埃及的纸草书。不过,这并不影响后人对古巴比伦灿烂文化的全面了解。古巴比伦人对于数学的发现和记载,也是采用这种独特的泥板书,在已经挖掘出的50万块古巴比伦泥板中,纯数学泥板有300块左右。

从这些存世发掘的数学泥板书中人们发现,古巴比伦人不仅早就形成“逢十进一”的概念,而且掌握了每隔六十进一的计数法。古代巴比伦人借助于图3中的符号,可以表示所有的整数,如图3所示。

图3

在德国柏林博物馆收藏的一块古巴比伦数学泥板书上记载了这样一道题目:兄弟10比伦的重量单位,其中1米那=60赛克尔）的银子,相邻的兄弟俩,比如老大和老二、老二和老三……所分银子的差相等,而且已知老八分到的银子是6赛克尔,求每人所得的银子数量。通俗转化的意思是:“10个兄弟分100两银子,一个比一个多,只知道每一级相差的数量都一样,但究竟相差多少不知道,现在第八个兄弟分到6两银子,问每级间相差多少。”这是一则涉及等差数列的问题,古巴比伦人给出的解题方法是如此巧妙简便,甚至连小学生也能理解。

他们的具体解答是:首先,要判断出10个兄弟分得的银子数,从老大到老十要么越来越多,要么越来越少。如果10个兄弟平均分这100两银子,则每人应该分到10两。而现在第八个兄弟分到了6两,说明只能是第二种情况,即老大分得多,往下是一个比一个少。其次,老大与老十的银子数之和=老二与老九的银子数之和=老三与老八的银子数之和=老四与老七的银子数之和=老五与老六的银子数之和,这样100两银子就分成了相等的5组,每组为20两。最后,就从老三与老八的银子数之和为20两入手。由老八的银子数6两,可求出老三的银子数为20-6=14（两）,这就说明,老三比老八多得14-6=8（两）。而老三与老八相差五级,因此可求得一级相差d=8÷5=1.6（两）。

上述问题如果用现在的符号语言来描述的话,相当于已知等差数列的项数n=10,和Sn=100,a8=6,求公差。通过分析可以看出,古代巴比伦人已经总结出等差数列的性质:am+an=ap+aq（m,n,p,q∈N*,且m+

还有一个非常有意思的例子,地质学家W.K.劳夫特斯于1854年发掘出两块泥板（称为森开莱泥板）其中一块上面刻着一个数列,用现代符号来写,前七个数是1,4,9,16,25,36,49。显然这是一个自然数平方的数列。49以后自然应该是64,81,…。但记载的却是1·4,1·21,…直到58·1。这一串数表示什么?猜测纷纷。事实上,这个问题只有在六十进位计数制中才能得到妥善的解释:

1·4=1×60+4=64=8×8;

1·21=1×60+21=81=9×9;

……

58·1=58×60+1=3 481=59×59。

（二）古埃及人的数学

古埃及人主要用纸草作为书写材料,纸草是尼罗河三角洲沼泽地盛产的一种水生植物,把这种草的茎依纵向剖成小薄片,然后压平晒干使之成为纸卷,可用于书写。由于埃及地区气候干燥,因此有些纸草能幸运地保存至今。产生于公元前1700年左右的《莫斯科纸草书》和《莱因德纸草书》（RhindPapyrus）是现在我们研究古埃及数学的主要来源。

首先我们来看看《莱因德纸草书》中的一个例子:10人分10斗玉米,从第二人开始,各人所得依次比前一人少。纸草书上给出的解法是:“取10人所得的平均值,即1;从10中减去1,得9。取差数的一半,得,再乘以9,得加平均值1,然后依次从各份中减去差数,直到最后一份。”10份依次是:

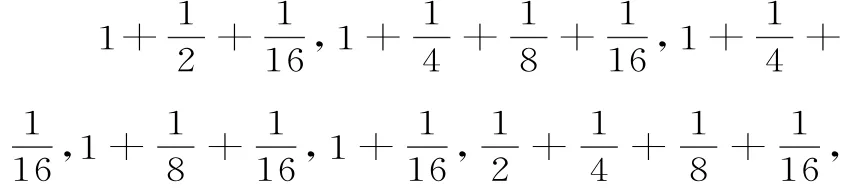
上述问题如果用现在的符号语言来描述的话,相当于已知等差数列的项数n=10,和法显然具有一般性,用我们的记号表示,即人已经总结出等差数列求和公式:Sn=na1+

虽然纸草书中的问题绝大部分是实用性质的,但也有例外,例如《莱茵德纸草书》第79题:“7座房,49只猫,343只老鼠,2 401颗麦穗,1 6807赫卡特。”（如图4）有人认为这是当时的一个数谜:7座房子,每座房里养7只猫,每只猫抓7只老鼠,每只老鼠吃7颗麦穗,每颗麦穗可产7赫卡特粮食,问房子、猫、老鼠、麦穗和粮食各数值总和。也有将房子、猫等解释为纸草书作者赋予不同幂次的名称,即房子表示一次幂,猫表示二次幂,老鼠表示三次幂,等等。无论如何,这是一个没有任何实际意义的几何级数求和问题,带有虚构的数学游戏性质。

到中世纪,意大利斐波那契在1202年发表了《算盘全书》,书中有这样一题:有七老妇人同往罗马,每人有七骡,每骡负七袋,每袋盛有七个面包,每个面包有七小刀随之,每小刀配有七鞘,问列举之物全数共有几何。显然都是与上述问题类似的等比数列的求和问题。

图4

（三）中国古代的数学

中国古代数学著作中有着丰富的数列知识,本文仅对其进行简单的梳理。约成书于公元1世纪的我国古代最著名的数学典籍《九章算术》（如图5）,它是中国古代第一部数学专著,其内容十分丰富,对战国、秦、汉时期的数学成就进行了系统总结。

我们就对《九章算术》均输章中的第17题、第19题进行简单的分析总结。

均输17:今有金棰,长五尺。斩本一尺,重四斤。斩末一尺,重二斤。问次一尺各重几何。意思是:五尺长的金鞭,各尺重量依次成等差数列,靠根的一尺斩下来称得重四斤,靠梢的一尺斩下来称得重二斤。求中间三尺各重多少。

术曰（后面给的解题方法）:令末重减本重,馀即差率也。又置本重,以四间乘之,为下第一衰。副置,以差率减之,每尺各自为衰。副置下第一衰以为法,以本重四斤遍乘列衰,各自为实。实如法得一斤。翻译成今天的数学符号语言就是:先求差率D=a5-a1,以“间数”4乘a5作为首项,然后从此项中依次减去D,得数列4a5,4a5-D,4a5-2D,4a5-3D,4a5-4D,再将所得数列各项同除以首项4a5,又同乘以a5,即得所求数列的各

图5

这个例子告诉我们,《九章算术》中已经有了朴素的等差数列公差的求法:d=+（n-1）d。

均输19:今有竹九节,下三节容四升,上四节容三升。问中间二节欲均容,各多少。意思是:有一根竹子,共9节,各节的容积依次成等差数列。已知较粗的下3节共容4升,较瘦的上4节共容3升。问各节的容积分别是多少。

术曰:以下三节分四升为下率,以上四节分三升为上率。上下率以少减多,馀为实。置四节、三节,各半之,以减九节,馀为法。实如法得一升,即衰相去也。下率一升少半升者,下第二节容也。简单梳理解法就是:先求,之后可求得公差（“衰四升,所以易得下第二节的容积。

这个例子告诉我们,《九章算术》中已经有等差数列通项的性质:2an=an-1+an+1,以及数列的前n项和的一条性质:若等差数列前m项和为Sm,最后k项和为Sk,则:

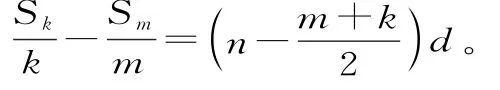
在中国古代,除《九章算术》以外,《孙子算经》（如图6）也是一部重要的数学著作。其成书大约在四、五世纪,也就是大约1500年前,作者生平和编写年不详。传本的《孙子算经》共三卷。这里面最著名的一道题目大概就是“鸡兔同笼”问题了,今天我们不研究“鸡兔同笼”问题,而是看另外一道题目:

图6

“出门望九堤”:今有出门望见九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色。问各几何。

这个问题是一个等比数列的问题,隐含着等比数列通项公式an=a1·qn-1的知识。

在课堂教学中我们一起去欣赏古今中外的数学史料和故事,感受数学的发展历程,不仅可以增进我们学习数学的信心,而且可以使我们了解到不同文化背景下的数学思想,理解数学的多元文化。当数学沿着历史的台阶走下神坛时,也揭开了数学文化神秘的面纱,真正向我们展示数学文化应有的人文价值。