多站精密定位技术研究

张旭东，刘 永，闫志闯

(1.72515部队，山东 济南 250000；2.西安测绘总站，陕西 西安 710054)

目前，美国的GPS卫星导航系统日臻成熟精确，俄罗斯的GLONASS卫星导航系统不断发展完善，欧盟的伽利略以及我国的北斗卫星导航系统正在快速发展。GNSS在各领域应用广泛，扮演的角色越来越重要。精密单点定位技术在交通运输、环境勘察、灾害预报、战场环境等方面作用明显。目前卫星采用非差、单差、双差等定位模式，精密单点定位(PPP)及其模糊度固定技术是当今GNSS领域的研究热点，该技术能够在全球范围内快速获取高精度框架坐标，但存在单点作业的局限性、非差模糊度难以固定及严重依赖高精度卫星轨道和钟差产品等问题，传统的非差精密定位只能得到模糊度浮点解，无法得到模糊度固定解，效果不好。但非差定位保留观测信息多、可保留原始的观测值等优点，非差定位观测量之间相互独立，同时还可以解算测站的绝对坐标。

针对模糊度固定问题，本文研究多个测站情况下的精密定位算法及其模糊度固定技术，先根据多个测站找到独立基线，在独立基线基础上由非差模糊度构建双差模糊度，采用LAMBDA算法搜索双差模糊度，根据非差模糊度与双差模糊度之间的映射关系，进而得到4个非差模糊度的约束关系，作为强约束，给其尽量大的权，从而在法方程中进行约束，得到模糊度约束解。从而解决多站条件下的模糊度固定问题，提高定位精度。

1 多站精密定位技术

1.1 精密单点定位观测模型

精密单点定位是利用卫星的双频非差载波相位和伪距观测量，采用IGS提供的卫星精密轨道和钟产品，采用严密的定位模型，解算相应框架下的绝对坐标。 精密单点定位通常需要双频伪距和载波组合观测，其双频消电离层组合可以表示为

PC=ρ+dTrop+δtr-δts+drel+

dgra+dwind+ΔPC,

LC=ρ+dTrop+amb+δtr-δts+drel+

dgra+dwind+ΔLC.

(1)

式中:PC表示双频伪距消电离层组合观测量；LC表示双频载波消电离层组合观测量；ρ为星地间距离；amb是非差模糊度参数，由于进行了消电离层组合，因此这里的模糊度失去了整数特性，后面作浮点解进行估计；dTrop为星地连线方向对流层改正延迟；δtr是接收机钟差改正；δts是卫星钟差改正；drel是相对论延迟改正；dgra是引力延迟改正；dwind是相位缠绕改正；ΔPC是双频伪距消电离层组合的测量误差；ΔLC是双频载波消电离层测量误差。此外，对站点位置及卫星位置有关的改正量体现在星地间距离ρ中。

1.2 非差模糊度约束基本原理

1.2.1 独立基线(模糊度)的选择

在本文中独立基线采用最大固定可能法。对于双差模糊度的选择，任何超过10 min观测弧段的双差模糊度可以作为备选值，它的宽巷模糊度可以使用相关相位和伪距观测值通过MW方法进行估计，其固定可能性(固定到最近整数的可能性)可以用式(2)进行计算。

(2)

(3)

式中:b和σ2是宽巷模糊度的估值和它的方差；I是b最近的整数。

对于给定的置信水平α，如0.1%，如果P0>1-α，模糊度能够被固定到最近整数，否则，将不能被固定。如果这个步骤宽巷不能被固定，那么窄巷也不能被固定。因此，仅仅那些固定宽巷的模糊度才能够作为固定的下一个步骤。

1.2.2 双差LC组合模糊度

精密单点定位为消除一阶项的电离层，采取无电离层的LC组合公式，设测站k对于卫星i的LC组合为

(4)

(5)

为了进行模糊度固定，双差LC组合模糊度可以用宽巷和窄巷表示为

(6)

1.2.2.1 宽巷固定

设接收机k和卫星i的宽巷和伪距观测值为

(7)

从式(7)中，每个历元从观测方程获得的宽巷模糊度为

(8)

第j历元的宽巷模糊度的估值和中误差为

(9)

1.2.2.2 窄巷固定

在宽巷模糊度固定后，窄巷模糊度的估值和中误差表示为

(10)

2 数据实验与分析

2.1 实验数据概况

采用2015年年积日005的35个全球IGS测站观测数据进行实验，精密星历和钟差采用IGS官方发布的高精度产品。在进行非差映射双差过程中，首先根据两个测站距离由近及远进行排列，同时考虑基线之间的独立性。在选择独立基线后，逐颗卫星选择独立的双差模糊度，选择准则是双差模糊度观测弧长由大到小，且必须是独立的双差模糊度。根据上述原则，实验中采用的35个全球IGS测站及其独立基线图表示为图1。

2.2 定位结果分析

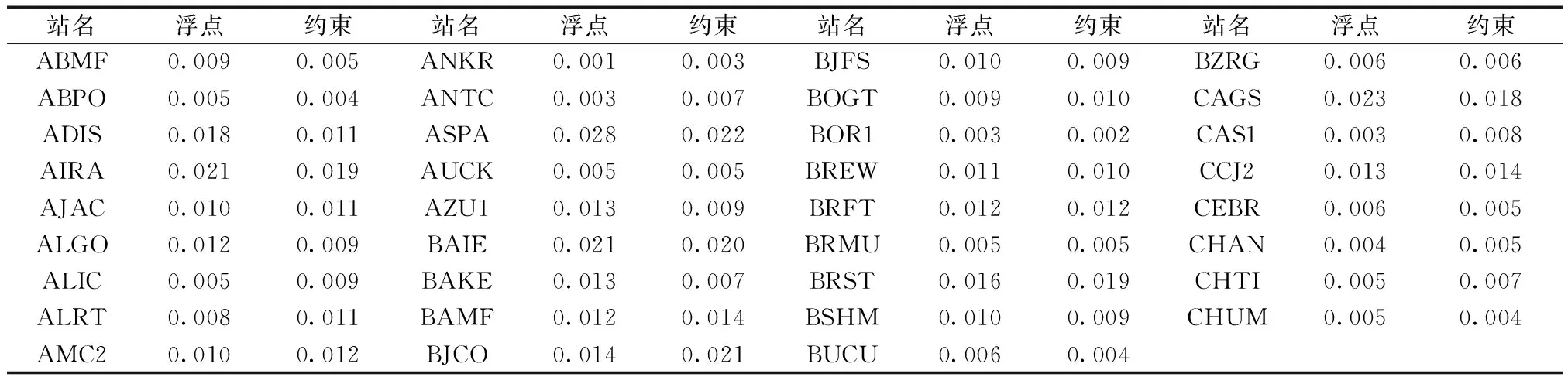
本实验采用多站非差定位模式，35个测站同时进行定位，根据模糊度是否约束，可以分为浮点解和约束解两种模式，图2和图3分别给出两种模式下定位精度与IGS周解之间的差异。 表1表示浮点解与模糊度约束解三维方向差异。

图1 IGS测站及其独立基线选择图

由实验结果可以看出，多站精密定位能够达到较高的定位精度，无论模糊度是否约束，定位精度都能够达到厘米甚至毫米级。从图1和图2中看出，模糊度约束解与浮点解相比，在E和N方向精度有所提高，而在U方向，精度改善有限，精度甚至可能有所降低。总体上看，E和N方向定位精度要优于U方向定位精度。从表1可以看出，采用模糊度约束方法固定部分模糊度，大部分测站3D精度有所提高，但也有部分测站精度有所降低，但都在mm量级。总体上看，采用模糊度约束方法整体上能够提高多站定位精度。

图2 浮点模糊度定位结果与IGS结果差异

图3 部分模糊度约束后结果与IGS结果差异

3 结 论

本文利用全球35个IGS站进行多站精密定位实验，通过选取独立基线并利用非差映射双差的方法进行模糊度约束解实验，可以得到以下结论：

1)本文使用的多站定位方法，无论是浮点解还是模糊度约束解，都能够获取cm甚至mm级定位精度，且35个测站3D精度优于0.03 m。

2)模糊度约束解相比浮点解定位精度总体上有所提高，尤其是在E方向提高较为明显。U方向个别测站精度提高较为明显，但大部分并不明显，精度甚至可能有所降低。

3)浮点解尽管不如约束解精度高，但仍然达到了cm甚至mm级精度，分析原因，由于实验中采用的观测数据均为24 h观测量，因此观测时长较长，对于提高定位精度具有决定性影响。

4)从实验结果看，不同测站定位结果之间具有一定差异，有些测站定位结果与IGS差异在mm级，有些在cm级，甚至达到将近0.03 m，分析其原因，可能是有些观测模型改正不太完善，抑或是部分粗差没有处理完善，还要进一步分析其中的原因。