高光谱组合变换下土壤Cd含量GWR模型反演研究
雷宇斌,刘 宁,郭云开,刘 磊,李丹娜
(1.湖南省第二测绘院,湖南 长沙 410000;2.中国能源建设集团湖南省电力设计院有限公司,湖南 长沙 410007;3.长沙理工大学,湖南 长沙 410076)
为了充分挖掘光谱信息,需要进行光谱变换,提高光谱对于重金属的响应能力。目前常用的土壤光谱变换方法主要有一阶微分、二阶微分、倒数对数、包络线去除、多元散射校正、标准正态化、小波分析与傅里叶变换等[2-7]。
由于目前土壤高光谱反演模型往往忽略了重金属的变异程度,而本文研究区的重金属Cd元素的变异程度高达96%,传统未嵌入地理位置参数的模型难以对高度变异的Cd元素进行准确建模与预测,因此本文在光谱组合变换研究的基础上选取了能有效揭示土壤变异性空间关系的GWR模型来进行重金属Cd元素的反演研究。
1 数据的获取与处理
1.1 研究区概况
选取湖南浏阳市某硫铁矿区周边耕地为研究对象,该地区占地总面积234.5 km2,区域地貌以丘陵和低山坡为主,境内气候隶属于亚热带季风性湿润气候,热量充足,降水丰沛,光照较足,多年平均气温17 ℃。 该区域作为老工业基地,矿产资源丰富,己探明有磷矿石、菊花石、海泡石等矿物20多种。当地矿产资源开发的同时加剧了耕地土壤生态环境的破坏,为了人民生活、生产幸福安全,需要研究矿区周围耕地重金属污染程度,因此开展该区域耕地重金属污染评价与反演工作。
1.2 土壤与光谱数据采集
本次研究实验采用AvaFiled-3高精度光谱地物波谱仪采集土壤光谱数据,采集时间为2017年5月,测量前先进行白板校正,每个土壤样点采集数条光谱曲线,取平均值后作为该样点的实际光谱反射数据。土壤取样根据土壤质地、作物覆盖类型在试验区使用T型取土器采集5个土样点,采样点位根据实地情况呈蛇形分布,所采集的土样使用密封装置带回实验室,并对每个样点进行相应行编号与简单的信息记录。实验时采用GPS定位仪器获取每个采样点的地理坐标,实验最终测得40个样方点,样点图如图1所示。

图1 采样点位置图
1.3 土壤重金属理化性质分析
重金属含量的测定依据《土壤环境监测技术规范》的相关标准进行。研究测定了Pb、Cu、Cd 3种重金属,结果如表1所示。表中三级标准均为国家土壤环境质量标准(GB15618-1995)所规定的土壤自然背景值与三级标准。
土壤科学中可用变异系数的数值来对土壤性质的变异程度进行相应等级划分,变异系数值在0~15%之间为小变异,16%~50%之间为中等变异,大于50%的则划分为高度变异[8],表中数据显示Cu、Pb的变异系数分别为50%与21%,Cd的变异系数高达96%,3种重金属元素中Cu元素的变异程度较低,Pb变异程度一般,Cd的变异最高,说明该区域重金属元素在空间上的变化程度相差较大。该区域属于矿区,适用于国家三级土壤质量标准,从表1中可以看出,Pb,Cu元素含量平均值均未超出标准,但Cd元素严重超标,其含量为国家三级土壤质量标准的3.5倍,判定该区域受Cd污染胁迫严重。因此,后续研究主要针对重金属Cd元素进行光谱变换与建模反演研究。

表1 重金属含量统计特征
2 光谱变换处理与分析
2.1 光谱变换
光谱变换处理的目的在于减弱光谱由于实验仪器设备、测量条件以及各种随机因素的影响所产生的噪声以提升建模精度。Kemper等人的研究发现,以5 nm、10 nm为重采样间隔对光谱进行重采样处理均可以在去除光谱噪声、减少冗余信息的同时较好的保持光谱数据特征[9]。本研究为了考虑更多的波段信息,最终在平滑之后选了5 nm的间隔来进行重采样处理。由于本次室内实验数据在2 350 nm处附近存在严重噪声,因此对此波段附近光谱数据做剔除处理,剔除前、后效果见图2。

图2 剔除前后土壤原始光谱曲线
光谱变换处理的方法较多,由于测量条件的不一所带来的噪声与误差尤为复杂,没有一种适用于各物质的、各成分分析的变换处理方法,因此在具体分析过程中需尽可能尝试多种数学变换方法以找到适用于某特定研究的最佳处理方法。本研究在对原始光谱数据进行常规变换处理方法的同时进行了组合变化处理,研究主要选取了一、二阶微分与开平方与开立方方法进行了结合,因为微分变换可以有效地消除背景噪声的影响并且能有效地提取出与研究变量相关的特征波段,乔星星[10]等的研究发现涉及微分处理后的光谱变换,尤其是进行开方、对数后再进行微分变换处理能最有效的提高土壤氮元素的光谱之间的相关性。本研究以此为参照在土壤重金属领域遥感反演领域进行尝试,具体光谱变换处理方法如表2所示。
A.恭喜你,你是一个绝佳的反派人选。虽然未必有人相信你的办事能力,但你非常有潜力,会有一鸣惊人的一天。你是一个可怕的敌人,有能力做反派主角。
2.2 相关性分析
相关系数的算式为
(1)
式中:R为相关系数,R的取值范围为[-1,1],|R|越趋近1代表变量X与Y的相关性越高。

表2 光谱数据变换处理方法
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。相关性分析在光谱敏感波段的选取方面应用广泛,利用SPSS软件来分析重金属元素Cd含量与光谱数据的相关性。将重金属Cd元素与各预处理变换后的光谱数据进行相关性分析的结果如图3所示,各光谱变换处理的最大相关性数值如表3所示。

图3 Cd元素与各光谱处理相关性曲线图

重金属最大相关性YSFDSDLOG-RECCREOSREOCREOSR-FD Cd-0.2760.4410.4310.2730.321-0.275-0.2740.425EOSR-SDEOCR-FDEOCR-SDREC-FDREC-SDLOG-FDLOG-SD0.4240.4160.421-0.4930.4110.4230.414
分析图3、表3中数据可知:倒数对数、开平方、开立方、连续统去除处理的光谱数据与Cd元素的相关性相比于原始数据的相关性并无改善;一、二阶微分方法处理后光谱数据与Cd元素的相关性相比原始光谱数据与重金属Cd元素0.276的相关性有所提高,相关性绝对值最大在0.41左右,且二阶微分相关性图像的整体稳定较好;组合变换预处理方法中只有倒数一阶微分的最大相关性绝对值接近0.5,其余组合变换如根号二阶微分、开立方二阶微分变换的最大相关性绝对值相比常规一、二阶微分处理并无有效提升,且相关性曲线的整体稳定性并不优于二阶微分相关性曲线。因此本研究最终选取二阶微分、倒数一阶微分处理方法中相关性较高的波段进行进一步建模分析并与原始光谱数据进行比较,备选的特征波段如表4所示。

表4 Cd元素特征波段选取
3 地理加权回归建模(GWR)
以往的各种土壤重金属回归建模过程中均未考虑到回归参数与空间位置的关系,但在实际研究过程中,数据建模的回归参数是随着地理位置而变化的,这时传统未考虑地理位置的全局回归模型参数只是研究区的平均值,不能反映整个研究区回归参数的真实空间特征。为了解决这一问题,Fortheringham等于1996年提出地理加权回归模型(Geographieally Weighted Regression Model,GWR),其主要改进是将研究数据的空间位置嵌入到了模型回归参数之中,并利用局部加权最小二乘的方法逐点对各参数进行估计,其中权值是回归点所在的地理空间位置到其他各观测点的地理空间位置之间的距离函数[11]。
3.1 模型原理
GWR模型是对普通线性回归模型的扩展,将数据的地理位置嵌入到回归参数之中,即:
yi=β0(ui+vi)+∑βk(ui,vi)xik+εi,
i=1,2,3,…,n.
(2)
式中:ui,vi为第i个采样点的坐标;βk(ui,vi)为第i个采样点上的第k个回归参数;εi是第i个样点的随机误差。
GWR模型当中每个样本点的回归权重值随着地理位置的变化而变化,权重函数用于描述位置因素对建模影响因素的大小[12]。由于big-square法在函数带宽范围之外的权重为0,更符合实际研究中会对回归参数几乎没有影响的数据删掉的情形,因此本研究选取big-square函数作为空间加权函数进行GWR建模分析,big-square加权函数的最优带宽以AIC法则确定:
(3)

由于GWR模型是基于数据的空间结构所建立的,不同土壤采样点的重金属对光谱的影响参数是不同的,表现出一定的空间异质性,而本研究区中重金属Cd含量的变异系数高达96%,属于高度变异,因此研究建立GWR模型进行探讨分析,其中28个样点进行建模,12个样点进行预测,地理加权回归建模基于GWR4.0软件实现。
3.2 建模结果分析
研究采用决定系数(R2)、均方根误差(RMSE)、以及相对分析误差(RPD)3种指标对模型的精度进行分析。决定系数也称拟合优度,表示自变量的平方和在因变量平方和中所占的比例,代表模型的所有解释变量对因变量的联合影响程度; MRE主要用于衡量与预测值同实测值之间的偏离程度,它是将预测值与实测值偏差的平方与样本数比值的平方根再除以样本的实测平均值,能有效地反映模型的预测误差;RPD的定义为实测值标准差与均方根误差之间的比值,其结果能够较好的评价所建立模型的适用泛化能力,模型的R2>0.5并且RPD>2时表明模型的预测能力较好;1.4 R2=SSR/SST, (4) (5) RPD=STD/RMSE. (6) GWR建模结果显示(见表5):①REC-SD光谱数据的建模效果最为理想,模型的R2高达0.82,MRE为29%,表明模型的预测精度达到71%,RPD为2.1,表明模型的预测能力较为优良;②SD光谱数据的建模结果中,有MRE为41%,表明模型的预测精度达到59%,预测精度一般,0.67的R2与1.5的RPD表明该模型对新数据的泛化能力较好;③YS光谱数据的建模效果较差,0.9的RPD与63%的MRE均表明该模型不可用于对样本点进行预测。 进一步分析可知,各光谱变换方式下Cd元素的GWR建模效果差异较大,变换后的光谱数据建模效果均优于原始光谱数据,且以倒数一阶微分变换的建模效果最优,说明对于原始光谱数据进行变换处理,尤其是倒数一阶微分变换处理能够有效地提高Cd元素GWR模型的预测精度。将重金属Cd元素REC-SD光谱数据建模的预测值与实测值绘制的散点图中显示(见图4),两者之间具有明显的线性趋势,预测值与实测值趋近于中心Y=X直线,表明样本点的预测结果比较理想。 表5 GWR建模方案与精度评价表 图4 预测值与实测值散点图 选取浏阳某矿区周边耕地土壤为研究对象,在对研究区污染状况进行统计分析的基础上选取受重金属Cd元素严重胁迫的土壤光谱数据进行处理与分析。研究结果显示,光谱组合变换方式中的REC-SD处理能有效提升重金属Cd元素含量与光谱数据的相关性,其建立的GWR模型精度均优于YS与SD光谱数据模型,研究结果表明光谱组合变换处理的可行性与优越性以及高度变异Cd元素GWR建模反演的适用性,为土壤高光谱数据的变换处理提供了一定参考价值,也为高度变异元素的反演建模建立了新的思路。但本研究仅采用了较为常见的10种数学组合变换,虽取得了一定效果但数学组合变换方法不胜枚举,且受条件限制只研究了Cu、Pb、Cd 3种重金属元素,其余元素变异对光谱变换的影响亟需进一步研究,今后可深入研究以寻求效果更好且尤为普适的变换方法。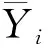


4 结束语

