双SCARA机器人运动学及奇异性分析

申浩宇，刘艳梨，吴洪涛

（1.陕西国防工业职业技术学院 机电工程学院，西安 710300；2.南京航空航天大学 机电学院，南京 210016）

0 引言

当前，机器人技术在很多领域都得到了广泛的应用。其中，并联机器人系统具备着特有的高精度，高刚度，高承载力，自重负荷小等多方面优点，自问世以来，就引起了极大的关注。近些年，有关并联机器人的研究热潮更是被不断地掀起[1～3]。

伴随着研究的深入，并联机器人的构型越来越多。在种种并联机器人的构型中，平面五杆机构的机械结构相对简单，并且运动学分析难度较低。在一些特定的工业场合，例如涉及到大量微小零部件的装配作业，平面五杆机构便于控制，重复定位能力高，成本低等方面的优势能够被更为明显的体现出来[4～8]。因此，以平面五杆机构为基本构型的并联机器人的研究受到了越来越多研究人员的关注[9～11]。例如，由三菱电机公司开发的RP-AH系列“双SCARA”机器人已经实现了产业化和商业化，由加拿大ETS学院开发的DexTAR机器人也非常适用于装配金属球等小零件的作业[12,13]。伴随着技术的不断完善和发展，该平面并联机器人技术必然会被更为广泛地应用在工业自动化生产领域中。

并联机器人的奇异性分析是一个重要的研究内容，尤其在机器人的机构设计中占有非常重要的地位。当机器人处于奇异位形时，会减少或增加一个或多个自由度，机构的运动状况会因此受到很大的影响。因此，奇异性分析在并联机器人的研究中十分重要，可为机构设计及优化提供必要的依据。

本文在平面五杆机构的基础上，提出了一种新型的双SCARA机器人。针对该机器人，进行了运动学求解，得到了正向运动学的解析解, 进一步获得了关节速度向量和末端速度向量之间的两个雅可比矩阵。然后,在给定几何参数的前提下，根据机器人雅可比矩阵的行列式对该平面并联机器人进行了奇异性分析，利用关节变量得到了反映机器人奇异位形的奇异性曲面。

1 双SCARA机器人结构

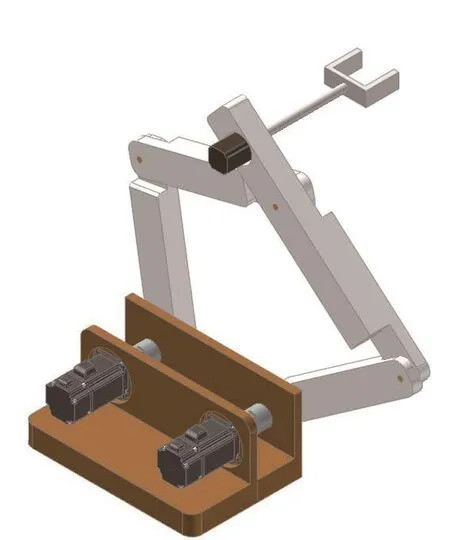
图1 双SCARA机器人的CAD模型

双SCARA机器人的结构如图1所示，由4个连杆及其支架，三个电机及末端手爪组成，连杆之间，连杆与支架之间均为旋转副连接。该机器人有三个自由度，可以实现平面上沿着两个坐标轴（X轴、Y轴）方向上的平动和绕着一个坐标轴（Z轴）的转动。需要指出的是，X-Y平面内的平动是由该机器人机构中的平面五杆机构的运动来实现的，而末端抓手的转动则是由轴3，通过安装在连杆4上的一个电机来实现的。

2 正向运动学模型

在正向运动学问题中，即是给定机器人的关节变量，求解出机器人末端的位置和姿态。对于并联机器人而言，通常情况下，正向运动学求解与反向运动学求解相比，难度更大。但是对于本文中提到的双SCARA并联机器人，由于其比较简单的机械结构，正向运动学的求解可以通过解析的形式表达出来。

机器人的机构简图如图2所示，Oi表示连杆在支架上的固定点，Li表示连杆i的长度，θi表示关节i的旋转角度。机器人末端的位置和姿态由X=[XD，YD，α]来表示，关节变量由θ=[θ1，θ2，θ3]来表示。正向运动学求解问题，即是给定关节变量θi，求解X=[XD，YD，α]。

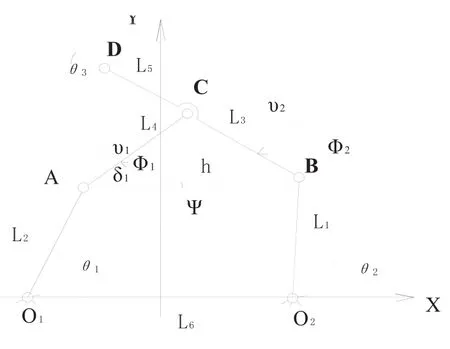
图2 双SCARA机器人的运动学简图

通过图2，可以得到以下的推导内容。

机器人末端的位置D点的坐标为：

其中：

两个关节点A和B的位置坐标可以通过关节变量θi表示为以下形式：

式(1)中，变量1δ由下式给定：

其中：

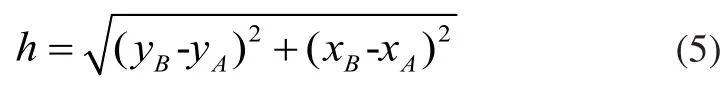
式(3)中的符号“±”表示机器人的两种工作模式，从而该机器人拥有两组正解，最后，机器人末端的姿态角α可以由下式给定：

此处：

式(1)和式(6)即为双SCARA机器人的正向运动学方程。

3 基于雅克比矩阵的奇异性分析

根据Gosselin和Angeles提出的奇异性分析方法，由并联机器人的运动学方程，该机器人的关节输入向量和末端输出向量之间存在着是一个非线性的运动学约束关系：

在本文案例中，上式是一个三维方程，式(8)对时间进行一阶求导，即可得到输入速度向量和输出速度向量之间的关系：

此处，Jx和Jθ均是三维的雅克比矩阵。当矩阵Jx和Jθ的发生奇异时，机器人处于奇异位形。在对Jx和Jθ进行奇异性分析的基础上，可以把并联机器人的奇异位形分为三类：

第一类奇异：称为逆运动学奇异, 顾名思义，即当det(Jθ)=0时的奇异性。此时Jθ奇异，并联机构失去至少一个自由度。这种奇异位形发生在机构的工作空间边界，也称为边界奇异。

第二类奇异：称为正运动学奇异。即当det(Jx)=0的奇异性。此时Jx奇异，当所有的驱动关节无输入时，并联机构末端依然可产生微小运动。从而，并联机构至少获得了一个自由度。

第三类奇异：称为综合奇异。当Jx和Jθ行列式同时为零时的奇异性。此时，所有关节均无输入时，末端还能产生微小运动；而当所有的关节均有输入时，末端可以依然静止。

4 雅克比矩阵的建立

将该双SCARA机器人的正向运动学方程改为式(8)所示的形式：

对式(10)进行一阶求导，得到式(9)的形式：

此处：

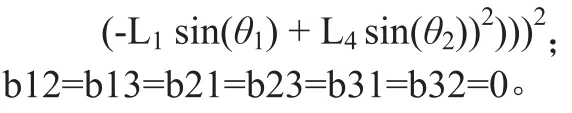
在给定机器人各个连杆的几何参数的前提下通过雅克比矩阵Jθ和Jx行列式的值得表达式，即可得到使得雅克比矩阵行列式值为0的奇异位形曲面。

5 算例分析

取双SCARA机器人结构参数：L1=L2=L3=L4=L5=1m，L6=1.5m。三个关节运动范围均为：0≤θ1，θ2，θ3≤2π。在Mathematics 9.0的软件环境下编写了程序，对矩阵Jθ和矩阵Jx的行列式值为零的曲面进行了绘制，三个关节角使得矩阵Jθ的行列式值为零的变化曲面如图3所示，三个关节角使得矩阵Jx的行列式值为零的变化曲面如图4所示。

图3 det(Jθ)为0时的三个关节角的变化曲面

图4 det(Jx)为0时的三个关节角的变化曲面

当关节角θ1，θ2，θ3的取值位于图3所示曲面上时，det(Jθ)为0，双SCARA机器人处于逆运动学奇异位形。当关节角θ1，θ2，θ3的取值位于图3所示曲面上时，det(Jx)为0，双SCARA机器人处于正运动学奇异位形。当三个关节角的取值位于图3和图4曲面的相交面上时，即det(Jθ)和det(Jx)同时为0，此时，机器人处于综合奇异位形。

6 结论

针对提出的双SCARA并联机器人机构，进行了正向运动学建模及雅克比矩阵的建立。利用雅克比矩阵的行列式值，对其奇异位形进行了分类。最后，在给定结构参数的情况下，针对一个仿真案例，在Mathematic9.0中编制了奇异曲面绘制程序，绘制了该双SCARA并联机器人的奇异性曲面。通过该方法，可以在双SCARA并联机器人的设计过程中，及时对给定结构参数下的机器人奇异位形进行预测，从而为进一步实现机器人的轨迹规划和工作空间优化提供了依据。